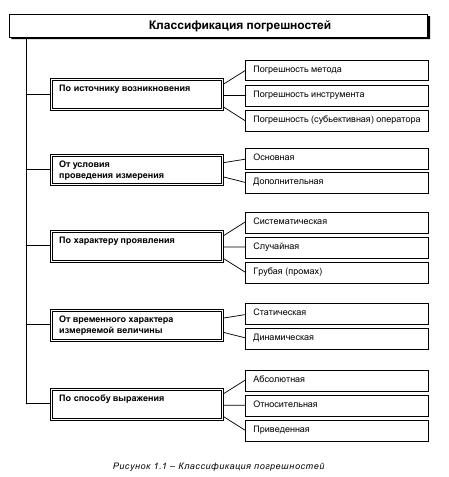
Укажите виды измерений по способу выражения результатов измерений

Измерение является важнейшим понятием в метрологии. Это организованное действие человека, выполняемое для количествен-ного познания свойств физического объекта с помощью определения опытным путем значения какой-либо физической величины [20].

Существует несколько видов измерений. При их классификации обычно исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов.

По характеру зависимости измеряемой величины от времени измерения разделяются на

статические, при которых измеряемая величина остается постоянной во времени;

динамические, в процессе которых измеряемая величина изменяется и является непостоянной во времени.

Статическими измерениями являются, например, измерения размеров тела, постоянного давления, динамическими — измерения пульсирующих давлений, вибраций.

По способу получения результатов измерений их разделяют на

Прямые — это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных. Прямые измерения можно выразить формулой , где — искомое значение измеряемой величины, а — значение, непосредственно получаемое из опытных данных.

При прямых измерениях экспериментальным операциям подвергают измеряемую величину, которую сравнивают с мерой непосредственно или же с помощью измерительных приборов, градуированных в требуемых единицах. Примерами прямых служат измерения длины тела линейкой, массы при помощи весов и др. Прямые измерения широко применяются в машиностроении, а также при контроле технологических процессов (измерение давления, температуры и др.).

Косвенные — это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле , где — искомое значение косвенно измеряемой величины; — функциональная зависимость, которая заранее известна, — значения величин, измеренных прямым способом.

Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить непосредственно или когда прямое измерение дает менее точный результат. Роль их особенно велика при измерении величин, недоступных непосредственному экспериментальному сравнению, например размеров астрономического или внутриатомного порядка.

Совокупные — это производимые одновременно измерения нескольких одноименных величин, при которых искомую определяют решением системы уравнений, получаемых при пря-мых измерениях различных сочетаний этих величин.

Примером совокупных измерений является определение массы отдельных гирь набора (калибровка по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь).

Пример. Необходимо произвести калибровку разновеса, состоящего из гирь массой 1, 2, 2*, 5, 10 и 20 кг (звездочкой отмечена гиря, имеющая то же самое номинальное значение, но другое истинное). Калибровка состоит в определении массы каждой гири по одной образцовой гире, например по гире массой 1 кг. Для этого про-ведем измерения, меняя каждый раз комбинацию гирь (цифры показывают массу отдельных гирь, — обозначает массу образцовой гири в 1 кг):

и т.д.

Буквы означают грузики, которые приходится прибавлять или отнимать от массы гири, указанной в правой части уравнения, для уравновешивания весов. Решив эту систему уравнений, можно определить значение массы каждой гири.

Совместные — это производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимостей между ними.

В качестве примера можно назвать измерение электрического сопротивления при 20 0 С и температурных коэффициентов измерительного резистора по данным прямых из-мерений его сопротивления при различных температурах.

По условиям, определяющим точность результата, измерения делятся на три класса:

1. Измерения максимально возможной точности, достижимой при существующем уровне техники.

К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например абсолютного значения ускорения свободного падения, гиромагнит-ного отношения протона и др.).

К этому же классу относятся и некоторые специальные изме-рения, требующие высокой точности.

2. Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого за-данного значения.

К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения.

3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений.

Примерами технических измерений являются измерения, выполняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др.

По способу выражения результатов измерений различают абсолютные и относительные измерения.

Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант.

Примером абсолютных измерений может служить определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате.

Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.

В качестве примера относительных измерений можно привести измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м 3 воздуха к количеству водяных паров, которое насыщает 1 м 3 воздуха при данной температуре.

Основными характеристиками измерений являются: принцип измерений, метод измерений, погрешность, точность, правильность и достоверность.

Принцип измерений — физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.

Метод измерений — совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства.

Погрешность измерений — разность между полученным при измерении X’ и истинным Q значениями измеряемой величины:

Погрешность вызывается несовершенством методов и средств измерений, непостоянством условий наблюдения, а так-же недостаточным опытом наблюдателя или особенностями его органов чувств.

Точность измерений — это характеристика измерений, отражающая близость их результатов к истинно-му значению измеряемой величины.

Количественно точность можно выразить величиной, обратной модулю относительной погрешности:

Например, если погрешность измерений равна , то точность равна .

Правильность измерения определяется как качество измерения, отражающее близость к нулю систематических погрешностей результатов (т.е. таких погрешностей, которые остаются постоян-ными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в част-ности, от того, насколько действительный размер единицы, в ко-торой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.

Важнейшей характеристикой качества измерений является их достоверность; она характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, не представляют ценности и в ряде случаев могут служить источником дезинформации.

Источник

1.4. Виды измерений по метрологии

Цель измерения – получение значения этой величины в форме, наиболее удобной для использования. Классификация измерений

Содержание:

По характеристике точности

Равноточные измерения – ряд измерений какой-либо величины, выполненных в одинаковых условиях.
Неравноточные измерения – ряд измерений, выполненных СИ различной точности и в разных условиях.

По количеству измерительной информации

Однократные измерения – число измерений равно числу измеряемых величин.
Многократные измерения – минимальное число измерений величины больше трех.

По выражению результата измерений

Абсолютные измерения — это такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна E =mc 2 масса (m) – основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) – физическая константа.
Относительные измерения — установление отношения измеряемой величины к однородной, применяемой в качестве единицы.
Прямые измерения – непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.
Косвенные измерения — искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью.

По способу получения результатов измерений

Совместные измерения — измерения одновременно двух или нескольких разноименных величин для нахождения зависимости между ними.
Совокупные измерения – это проводимые одновременно измерения одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при измерениях этих величин в различных состояниях.

По метрологическому назначению

Технические измерения – с помощью рабочих средств. Применяются в науке и технике, с целью контроля параметров изделий, процессов и т.д.
Метрологические измерения – при помощи эталонов и образцовых средств измерения, с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.

По характеру изменения измеряемой величины

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

Статические измерения — величины практически постоянны.
Динамические измерения — величины, в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

Источник

Виды измерений

1) По характеру зависимости измеряемой величины от времени:

а) статические — имеют место, когда измеряемая величина практически постоянна (измерения размеров тела, постоянного давления);

б) динамические, связанные с величинами, которые в процессе измерений претерпевают те или иные изменения (измерения пульсирующих давлений, вибраций).

2) По способу получения результатов:

а) Прямые измерения — измерения, при которых искомое значение физической величины находят непосредственно из опытных данных путем ее непосредственного сравнения с мерой. (измерение давления, температуры и др.).

б) Косвенные измерения — измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят через преобразование или через установленную формулу ( определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения).

в) Совокупные измерения — это производимые одновременно измерения нескольких одноименных величин, характеризующих Данный предмет или изделие, при которых искомую определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин ( определение массы отдельных гирь набора (или прогнозирование погоды на основе замеров силы ветра, влажности воздуха, фронтов и т.п).

г) Совместные измерения — это производимые одновременно измерения двух или нескольких неоднородных физических величин для нахождения зависимостей между ними (измерение электрического сопротивления при определенных температурных параметрах и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах).

3) По условиям, определяющим точность результата:

а) Измерения максимально возможнойточности, достижимой при существующем уровне техники.

К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например, абсолютного значения ускорения свободного падения и др.). К этому же классу относятся и некоторые специальные измерения, требующие высокой точности.

б) Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения.

К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого заранее заданного значения.

в) Технические измерения, в которых погрешность результата определяется характеристиками средств измерений.

4) По способу выражения результатов измерений:

а) Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант (определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате).

б) Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную (измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м» 3 воздуха к количеству водяных паров, которое насыщает 1 m j воздуха при данной температуре).

5) По характеру изменения измеряемой величины измерения:

а) Статические — применяют для измерения случайных процессов, а затем для определения среднестатистической величины;

б) Постоянные — используют для контроля непрерывных процессов.

6) По количеству измерительной информации измерения:

а) Однократные измерения — это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями.

б) Многократные измерения — характеризуются превышением числа измерений количества измеряемых величин. Преимущество многократных измерений — значительное снижение влияний случайных факторов на погрешность измерения.

Основными характеристиками измерений являются:

Принцип измерении — физическое явление или совокупность физических явлений, положенных в основу измерений (измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта).

Метод измерений — совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства.

Различают методы непосредственной оценки и методы сравнения .

При измерении методом непосредственной оценки искомое значение величины определяют непосредственно по отсчетному устройству средства измерения, которое проградуировано в соответствующих единицах.

Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (например, сравнение массы на рычажных весах). Отличительной чертой методов сравнения является непосредственное участие меры в процедуре измерения, в то время как в методе непосредственной оценки мера в явном виде при измерении не присутствует, а ее размеры перенесены на отсчетное устройство (шкалу) средства измерения заранее, при его градуировке. Обязательным в методе сравнения является наличие сравнивающего устройства.

Метод сравнения с мерой имеет несколько разновидностей: нулевой метод, дифференциальный метод, метод замещения и метод совпадений.

Нулевой метод (или метод полного уравновешивания) — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и встречного воздействия меры на сравнивающее устройство сводят к нулю.

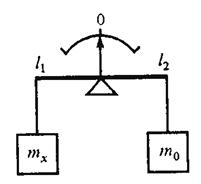
Например. Измерение массы на равноплечих весах, когда воздействие на весы массы m_х полностью уравновешивается массой гирь m₀ (рисунок 2).

Рисунок 2 – Метод полного уравновешивания

При дифференциальном методе полное уравновешивание не производят, а разность между измеряемой величиной и величиной, воспроизводимой мерой, отсчитывается по шкале прибора.

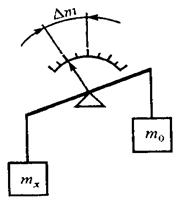
Например. Измерение массы на равноплечих весах, когда воздействие массы m_х на весы частично уравновешивается массой гирь m₀, а разность масс отсчитывается по шкале весов, градуированной в единицах массы (рисунок 3).

Рисунок 3 – Дифференциальный метод

В этом случае значение измеряемой величины m_х = m₀ + m, где m — показания весов

Метод замещения — метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой.

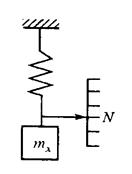
Например.Взвешивание на пружинных весах. Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу m_х замещают массой гирь m₀, подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае. При этом ясно, что m_х = m₀, (рисунок 4).

Рисунок 4 – Метод замещения

В методе совпадений разность между измеряемой величиной и величиной воспроизводимой мерой измеряют, используя совпадения отметок шкал или периодических сигналов.

Например. Измерение числа оборотов вала с помощью стробоскопа — вал периодически освещается вспышками света, и частоту вспышек подбирают так, чтобы метка, нанесенная на вал, казалась наблюдателю неподвижной. Метод совпадений, использующий совпадения основной и нониусной отметок шкал, реализуется в штангенприборах, применяемых для измерения линейных размеров.

Погрешность измерений — отклонение результата измерений от истинного значения измеряемой величины. Погрешность вызывается воздействием множества факторов, таких как: характер измеряемой величины, качество применяемых средств измерений, метод измерений, условия измерения (температура, влажность, давление и т.п.), индивидуальные особенности лица, выполняющего измерения, и др. Под влиянием этих факторов результат измерений будет отличаться от истинного значения измеряемой величины.

Точность измерений — качественная характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины.

Количественно точность можно выразить величиной «класс точности». Это характеристика, зависящая от способа выражения пределов допускаемых погрешностей средств измерений. Введение класса точности преследовало цель классификации средств измерений по точности. В настоящее время, когда схемы и конструкции средств измерений усложнились, а области применения средств измерений весьма расширились, на погрешность измерений стали существенно влиять и другие факторы: изменения внешних условий и характер изменения измеряемых величин во времени.

Погрешность измерительных приборов перестала быть основной составляющей погрешности измерений, и класс точности не позволяет в полной мере решать практические задачи, перечисленные выше. Область практического применения характеристики «класс точности» ограничена только такими средствами измерений, которые предназначены для измерения статических величин. В международной практике «класс точности» устанавливается только для небольшой части приборов.

Правильность измерений — качество измерений, отражающее близость к нулю систематических погрешностей в их результатах (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в частности, от того, насколько действительный размер единицы, в которой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.

Достоверность характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Поэтому такие вероятности следует рассматривать в качестве критериев достоверности контроля, чтобы в границах допуска правильно охарактеризовать параметры качества и безопасности.

Наличие погрешности ограничивает достоверность измерений, т.е. вносит ограничение в число достоверных значащих цифр числового значения измеряемой величины и определяет точность измерений. Характеристики погрешности измерений должны выбираться при контроле образцов продукции в соответствии с требованиями достоверности контроля.

Измерения как основной объект метрологии связаны в основном с физическими величинами:

Физическая величина — одно из свойств физического объекта, явления, процесса, который является общим в качественном отношении для многих физических объектов, отличаясь при этом количественным значением.

Физическая величина, которой по определению присвоено числовое значение, равное единице, называется единицей физической величины.

Различают основные и производные единицы.

Основные единицы физической величины выбираются произвольно, независимо от других единиц ( единица длины — метр, единица массы — килограмм, единица температуры — градус и т.д.)

Единицы, образованные с помощью формул, выражающих зависимость между физическими величинами, называют производными единицами. В этом случае единицы величин будут выражаться через единицы других величин. Например, единица скорости — метр в секунду (м/с), единица плотности — килограмм на метр в квадрате (кг/м 2 ).

Разные единицы одной и той же величины отличаются друг от друга своим размером. Такие единицы называют кратными (например, километр — 10 3 м, киловатт — 10 3 Вт) или дельными (например, миллиметр — 10 -3 м, миллисекунда — 10-3 с). Такие единицы получают умножением или делением независимой или производной единицы на целое число, обычно на 10.

Единицы физических величин объединяются по определенному принципу в системы единиц. Эти принципы заключаются в следующем: произвольно устанавливают единицы для некоторых величин, называемых основными единицами, и по формулам через основные получают все производные единицы для данной области измерений. Совокупность основных и производных единиц, относящихся к некоторой системе величин и образованная в соответствии с принятыми принципами, составляет систему единиц физических величии.

Многообразие систем единиц для различных областей измерений создавало трудности в научной и экономической деятельности как в отдельных странах, так и в международном масштабе. Поэтому возникла необходимость в создании единой системы единиц, которая включала бы в себя единицы величин для всех разделов физики.

Международная система единиц состоит из семи основных единиц, двух дополнительных единиц и необходимого числа производных единиц.

К основным относятся:

— единица длины — метр — длина пути, которую проходитсвет в вакууме за 1/299792458 долю секунды;

— единица массы — килограмм — масса, равная массе международного прототипа килограмма;

— единица времени — секунда — продолжительность9192631770 периодов излучения, соответствующего переходу между двумя уровнями сверхтонкой структуры основного состояния атома цезия-133 при отсутствии возмущения со стороны внешних полей;

— единица силы электрического тока — ампер — сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого ввакууме, создал бы между этими проводниками силу, равную 2 • 10

7 Н на каждый метр длины;

— единица термодинамической температуры — кельвин — часть термодинамической температуры тройной точки воды. Допускается также применение шкалы Цельсия;

— единица количества вещества — моль — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде углерода-12 массой 0,012 кг;

— единица силы света — кандела — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540- 10 12 Гц, энергетическая сила которого в этом направлении составляет 1/683 Вт/ср».

Три первые единицы (метр, килограмм, секунда) позволяют образовать производные единицы для измерения механических и акустических величин. При добавлении к указанным четвертой единицы — кельвина можно образовать производные единицы для измерений тепловых величин.

Единицы (метр, килограмм, секунда, ампер) служат основой для образования производных единиц в области электрических, магнитных измерений и измерений ионизирующих излучений. Единица моль используется для образования единиц в области физико-химических измерений.

Дополнительными единицами являются:

Единица плоского угла — радиан и единица телесного угла — стерадиан используются для образования производных единиц, связанных с угловыми величинами (например, угловая скорость, световой поток и др.).

ШКАЛЫ ИЗМЕРЕНИЙ

Шкала наименований – это качественная, а не количественная шкала, она не содержит нуля и единиц измерений (напр., шкала цветов).

Такие шкалы используется для классификации объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. В шкалах наименований оценивание осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствуют понятия нуля, «больше или меньше» и единицы измерения.

Шкала порядка – характеризует значение измеряемой величины в баллах (напр., шкала землетрясений; силы ветра и др.).

Она является монотонно изменяющейся и позволяет установить отношения «больше — меньше» между величинами, характеризующими это свойство. Нуль существует или не существует, но принципиально невозможно ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нельзя судить, во сколько раз больше или меньше конкретные проявления свойства.

Шкала интервалов – имеет условное нулевое значение, а интервалы устанавливают по согласованию (напр., шкала времени, шкала длины).

Данные шкалы являются дальнейшим развитием шкал порядка. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление, температурные шкалы.

Шкала отношений – имеет естественное нулевое значение, а единица измерений устанавливается по согласованию, в зависимости от требования точности измерения (напр., шкала веса).

С формальной точки зрения эта шкала является шкалой интервалов с естественным началом отсчета. К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет большое значение при измерении ФВ.

Источник