Укажите виды измерений по способу получения информации метрология

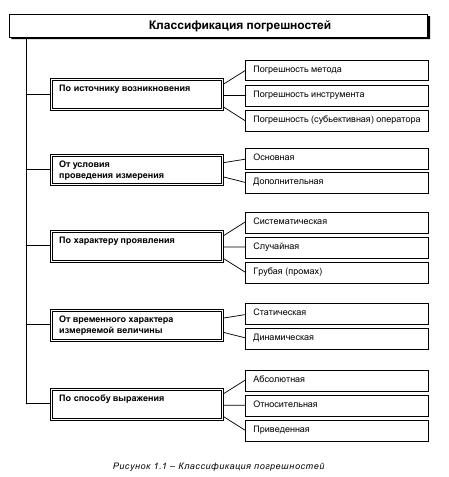
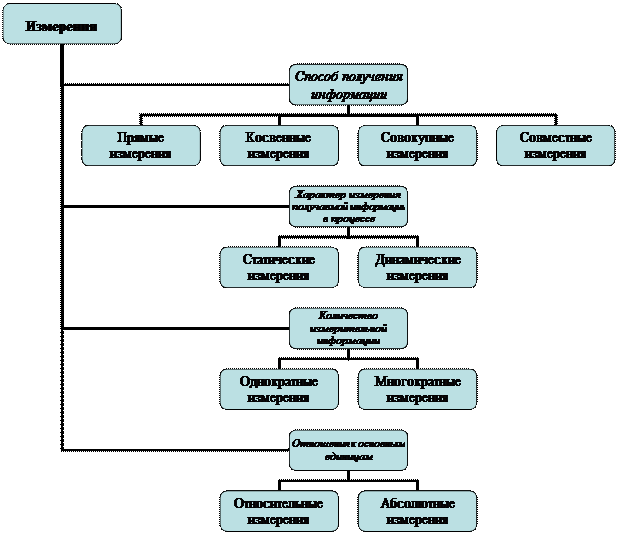
Классификация видов измерений

Измерения различают по способу получения информации, по характеру изменений измеряемой величины в процессе измерений, по количеству измерительной информации, по отношению к основным единицам.

По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения – это непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т. е. линейкой.

Косвенные измерения – отличаются от прямых тем, что искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью. Так, если измерить силу тока амперметром, а напряжение вольтметром, то по известной функциональной взаимосвязи всех трех величин можно рассчитать мощность электрической цепи.

Совокупные измерения – сопряжены с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину.

Совместные измерения – это измерения двух или более неоднородных физических величин для определения зависимости между ними.

Совокупные и совместные измерения часто применяют в измерениях различных параметров и характеристик в области электротехники.

По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т. д. Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения. Статические и динамические измерения в идеальном виде на практике редки.

По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения – это одно измерение одной величины, т. е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Преимущество многократных измерений – в значительном снижении влияний случайных факторов на погрешность измерения.

По используемому методу измерения – совокупности приемов использования принципов и средств измерений различают:

• метод непосредственной оценки;
• метод сравнения с мерой;
• метод противопоставления;
• метод дифференциальный;
• метод нулевой;
• метод замещения;
• метод совпадений.

По условиям, определяющим точность результата, измерения делятся на три класса: измерения максимально возможной точности, достижимой при существующем уровнетехники; контрольно-поверочные измерения, погрешность которых не должна превышать некоторое заданное значение; технические (рабочие) измерения, в которых погрешность результата измерения определяется характеристиками средств измерений.

Источник

Классификация измерений

Все измерения классифицируют (рис. 8.2):

• по способу получения информации;

• по характеру изменения получаемой информации в процессе измерения;

• по количеству измерительной информации;

• по отношению к основным единицам.

Рис. 8.2 Классификация измерений

По способу получения информации измерения разделя­ютсяна следующие виды:

1. Прямые измерения, при которых искомое значение измеряемой величины получают непосредственно (пу­тем сравнения величины с ее единицей). При прямых измерениях объект исследования приводят во взаимо­действие со средством измерений и по его показаниям отсчитывают значение измеряемой величины.

К прямым измерениям относятся измерение массы при помощи весов и гирь, силы тока — амперметром, температуры — термометром, измерение длины — ли­нейкой.

2. Косвенные измерения, при которых искомое значение величины определяют на основании прямых измере­ний других величин, функционально связанных извест­ной зависимостью с искомой величиной. Например, плотность тела можно определить по результатам измерений массы т и объема V:

ρ 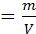(8.1)

а скорость при равномерном движении — по результатам измерений пройденного пути S и времени τ:

(8.2)

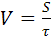
3. Совокупные измерения, при которых одновремен­но проводятся измерения нескольких одноименных величин и искомое значение величины, определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях, при этом число уравнений должно быть не меньше числа величин. Например, значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь.

4. Совместные измерения, при которых одновременно проводятся измерения двух или нескольких не од­ноименных величин для определения зависимости между ними, например, зависимость длины объекта от температуры.

По характеру изменения получаемой информациив про­цессе измерений измерения подразделяются на статичес­кие и динамические.

Статические измерения — это такие измерения, ког­да измеряемая величина принимается за неизменную на протяжении времени измерения, например, измерение размеров земельного участка.

Динамическое измерение — это измерение, в процессе которого измеряемая величина изменяется.

Развитие средств измерений и повышение их чувс­твительности позволяет сегодня обнаружить изменение величин, ранее считавшихся постоянными, поэтому раз­деление измерений на динамические и статические можно считать условным.

По количеству измерительной информацииизмерения делятся на однократные и многократные.

Однократные измерения выполняются один раз, а мно­гократные позволяют получить результат из нескольких следующих друг за другом измерений одного и того же объекта. При однократных измерениях показания средств измерений являются результатом измерений, погрешность используемого средства измерений определяет погреш­ность результата измерения. Применение многократных измерений позволяет повысить точность измерения до определенного предела.

По отношению к основным единицамизмерения делятся на абсолютные и относительные.

Абсолютные измерения основаны на прямых изме­рениях одной или нескольких основных величин или использовании значений физических констант. Например, определение массы в килограммах, количества вещест­ва—в молях, частоты — в герцах.

Относительные измерения — это измерения отноше­ния величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отно­шению к одноименной величине, принимаемой за исход­ную. Например, относительная влажность определяется как отношение упругости водяного пара, содержащегося в воздухе, к упругости насыщенного пара при той же температуре, и выражается в процентах.

Источник

1.4. Виды измерений по метрологии

Цель измерения – получение значения этой величины в форме, наиболее удобной для использования. Классификация измерений

Содержание:

По характеристике точности

• Равноточные измерения – ряд измерений какой-либо величины, выполненных в одинаковых условиях.
• Неравноточные измерения – ряд измерений, выполненных СИ различной точности и в разных условиях.

По количеству измерительной информации

• Однократные измерения – число измерений равно числу измеряемых величин.
• Многократные измерения – минимальное число измерений величины больше трех.

По выражению результата измерений

• Абсолютные измерения — это такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна E =mc 2 масса (m) – основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) – физическая константа.
• Относительные измерения — установление отношения измеряемой величины к однородной, применяемой в качестве единицы.
• Прямые измерения – непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.
• Косвенные измерения — искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью.

По способу получения результатов измерений

• Совместные измерения — измерения одновременно двух или нескольких разноименных величин для нахождения зависимости между ними.
• Совокупные измерения – это проводимые одновременно измерения одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при измерениях этих величин в различных состояниях.

По метрологическому назначению

• Технические измерения – с помощью рабочих средств. Применяются в науке и технике, с целью контроля параметров изделий, процессов и т.д.
• Метрологические измерения – при помощи эталонов и образцовых средств измерения, с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.

По характеру изменения измеряемой величины

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

• Статические измерения — величины практически постоянны.
• Динамические измерения — величины, в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

Источник

27.2. Виды измерений

Измерения различают по способу получения информации, по характеру изменений измеряемой величины в процессе измерений, по количеству измерительной информации, по отношению к основным единицам.

По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения — это непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.

Косвенные измерения отличаются от прямых тем, что искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью, Так, если измерить силу тока амперметром, а напряжение вольтметром, то по известной функциональной взаимосвязи всех трех названных величин можно рассчитать мощность электрической цепи.

Совокупные измерения сопряжены с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину.

Совместные измерения — это измерения двух или более неоднородных физических величин для определения зависимости между ними.

Совокупные и совместные измерения часто применяют в измерениях различных параметров и характеристик в области электротехники.

По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения — это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Обычно минимальное число измерений в данном случае больше трех. Преимущество многократных измерений — в значительном снижении влияний случайных факторов на погрешность измерения.

По отношению к основным единицам измерения делят на абсолютные и относительные.

Абсолютными измерениями называют такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна Е=тс 2 масса (m) — основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (c) — физическая константа.

Относительные измерения базируются на установлении отношения измеряемой величины к однородной, применяемой в качестве единицы. Естественно, что искомое значение зависит от используемой единицы измерений.

С измерениями связаны такие понятия, как «шкала измерений», «принцип измерений», «метод измерений».

Шкала измерений — это упорядоченная совокупность значений физической величины, которая служит основой для ее измерения. Поясним это понятие на примере температурных шкал.

В шкале Цельсия за начало отсчета принята температура таяния льда, а в качестве основного интервала (опорной точки) — температура кипения воды. Одна сотая часть этого интервала является единицей температуры (градус Цельсия). В температурной шкале Фаренгейта за начало отсчета принята температура таяния смеси льда и нашатырного спирта (либо поваренной соли), а в качестве опорной точки взята нормальная температура тела здорового человека. За единицу температуры (градус Фаренгейта) принята одна девяносто шестая часть основного интервала. По этой шкале температура таяния льда равна + 32°F, а температура кипения воды + 212°F. Таким образом, если по шкале Цельсия разность между температурой кипения воды и таяния льда составляет 100°С, то по Фаренгейту она равна 180°F. На этом примере мы видим роль принятой шкалы как в количественном значении измеряемой величины, так и в аспекте обеспечения единства измерений. В данном случае требуется находить отношение размеров единиц, чтобы можно было сравнить результаты измерений, т.е. t o F/t°C.

В метрологической практике известны несколько разновидностей шкал: шкала наименований, шкала порядка, шкала интервалов, шкала отношений и др.

Шкала наименований — это своего рода качественная, а не количественная шкала, она не содержит нуля и единиц измерений. Примером может служить атлас цветов (шкала цветов). Процесс измерения заключается в визуальном сравнении окрашенного предмета с образцами цветов (эталонными образцами атласа

цветов). Поскольку каждый цвет имеет немало вариантов, такое сравнение под силу опытному эксперту, который обладает не только практическим опытом, но и соответствующими особыми характеристиками зрительных возможностей

Шкала порядка характеризует значение измеряемой величины в баллах (шкала землетрясений, силы ветра, твердости физических тел и т.п.).

Шкала интервалов (разностей) имеет условные нулевые значения, а интервалы устанавливаются по согласованию. Такими шкалами являются шкала времени, шкала длины.

Шкала отношений имеет естественное нулевое значение, а единица измерений устанавливается по согласованию. Например, шкала массы (обычно мы говорим «веса»), начинаясь от нуля, может быть градуирована по-разному в зависимости от требуемой точности взвешивания. Сравните бытовые и аналитические весы.

Источник