Информатика
Алгоритмы и способы их описания.
Алгоритм — это система точных и понятных предписаний о содержании и последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа.
Примеры: правила сложения, умножения, решения алгебраических уравнений и т.п.
1.Универсальность (массовость) — применимость алгоритма к различным наборам исходных данных.
2.Дискретность — процесс решения задачи по алгоритму разбит на отдельные действия.
3.Конечность — каждое из действий и весь алгоритм в целом обязательно завершаются.
4.Результативность — по завершении выполнения алгоритма обязательно получается конечный результат.
5.Выполнимость (эффективность) — результата алгоритма достигается за конечное число шагов.
6.Детерминированность (определенность) — алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно. Т.е. одно и то же предписание после исполнения должно давать один и тот же результат.
7.Последовательность – порядок исполнения команд должен быть понятен исполнителю и не должен допускать неоднозначности.
1. вычислительные алгоритмы , работающие со сравнительно простыми видами данных, такими как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным;
2. информационные алгоритмы , представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных);
3. управляющие алгоритмы , генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют.
По типу передачи управления алгоритмы бывают: основные (главные выполняемые программы) и вспомогательные (подпрограммы).
Для задания алгоритма необходимо описать следующие его элементы:
1.набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;
3.правило непосредственной переработки информации (описание последовательности действий);
5.правило извлечения результатов.
Способы описания алгоритмов.
Символьный, когда алгоритм описывается с помощью специального набора символов (специального языка).
Словесная форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного.
Графическая запись с помощью блок-схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Графическая запись алгоритма имеет ряд преимуществ: каждая операция вычислительного процесса изображается отдельной геометрической фигурой и графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали.
Правила создания блок – схем:
1.Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки.
2.Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз.
3.В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков.
4.Из блока (кроме логического) может выходить только одна линия.
5.Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии.
6.Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить.
7.Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки.
В линейном алгоритме операции выполняются последовательно, в порядке их записи. Каждая операция является самостоятельной, независимой от каких-либо условий. На схеме блоки, отображающие эти операции, располагаются в линейной последовательности.
В алгоритме с ветвлением предусмотрено несколько направлений (ветвей). Каждое отдельное направление алгоритма обработки данных является отдельной ветвью вычислений. Направление ветвления выбирается логической проверкой, в результате которой возможны два ответа:
1.«да» — условие выполнено.
2.«нет» — условие не выполнено.
Циклические алгоритмы содержат цикл – это многократно повторяемый участок алгоритма.Различают циклы с предусловием и постусловием.Также циклы бывают детерминированные и итерационные.Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров (некоторых переменных), участвующих в вычислениях.
Источник
Алгоритмы
Алгоритмы. Способы записи алгоритмов
Выделяют три наиболее распространенные на практике способа записи алгоритмов:
- словесный (запись на естественном языке);
- графический (запись с использованием графических символов);
- программный (тексты на языках программирования).
Словесный способ записи алгоритмов
Словесный способ – способ записи алгоритма на естественном языке. Данный способ очень удобен, если нужно приближенно описать суть алгоритма. Однако при словесном описании не всегда удается ясно и точно выразить логику действий.
В качестве примера словесного способа записи алгоритма рассмотрим алгоритм нахождения площади прямоугольника
где S – площадь прямоугольника; а, b – длины его сторон.
Очевидно, что a, b должны быть заданы заранее, иначе задачу решить невозможно.
Словестный способ записи алгоритма выглядит так:
- Начало алгоритма.
- Задать численное значение стороны a.
- Задать численное значение стороны b.
- Вычислить площадь S прямоугольника по формуле S=a*b.
- Вывести результат вычислений.
- Конец алгоритма.
Графический способ описания алгоритмов
Для более наглядного представления алгоритма используется графический способ. Существует несколько способов графического описания алгоритмов. Наиболее широко используемым на практике графическим описанием алгоритмов является использование блок-схем. Несомненное достоинство блок схем – наглядность и простота записи алгоритма.
Каждому действию алгоритма соответствует геометрическая фигура (блочный символ). Перечень наиболее часто употребляемых символов приведен в таблице:
| Название символа | Обозначение и пример заполнения | Пояснения |
| Пуск-останов |  | Начало, завершение алгоритма или подпрограммы |
| Ввод-вывод данных |  | Ввод исходных данных или вывод результатов |
| Процесс |  | Внутри прямоугольника записывается действие, например, расчетная формула |
| Решение |  b» width=»219″ height=»65″/> b» width=»219″ height=»65″/> | Проверка условия, в зависимости от которого меняется направление выполнения алгоритма |
| Модификация |  | Организация цикла |
| Предопределенный процесс |  | Использование ранее созданных подпрограмм |
| Комментарий |  | Пояснения |
- блок Процесс обозначает вычислительный процесс и применяется для обозначения действия или последовательности действий, изменяющих значения переменных или данных
- блок Решение обозначает проверку условия
Если условие выполняется, то есть a>b, то следующим выполняется действие по стрелке «Да». Если условие не выполняется, то осуществляется переход по стрелке «Нет».
- блок Модификация используется для организации циклических (повторяющихся) действий.
- блок Предопределенный процесс используется для указания обращений к ранее созданным алгоритмам и программам, в том числе и библиотечным подпрограммам.
- блок Ввод-Вывод. При решении задачи на компьютере ввод исходных данных может осуществляться различными способами, например, с клавиатуры, с жесткого диска, с флэш-карты т. д. Задание численных значений исходных данных называется вводом, а отображение результатов расчета на экране монитора или с помощью принтера на бумаге – выводом. Если ввод-вывод не привязан к конкретному устройству, то обозначается параллелограммом. Если необходимо указать конкретное устройство ввода или вывода, то используются специальные геометрические фигуры.
 |  |  |
| устройство ввода или вывода | дисплей | магнитный диск |
В качестве примера графического способа описания алгоритмов с помощью блок-схем запишем алгоритм нахождения площади прямоугольника:
Внутри каждого блока записывается соответствующее действие. Последовательность выполнения задается соединительной линией со стрелочкой.
Последовательность выполнения сверху вниз и слева направо принята за основную.
Если в алгоритме не нарушается основная последовательность, то стрелочки можно не указывать. В остальных случаях последовательность выполнения блоков обозначается стрелочкой обязательно. В нашем примере основная последовательность выполнения – сверху вниз.
Программный способ записи алгоритмов
Способ записи алгоритмов с помощью блок-схем нагляден и точен для понимания сути алгоритма, тем не менее, алгоритм предназначен для исполнения на компьютере, а язык блок-схем компьютер не воспринимает. Поэтому алгоритм должен быть записан на языке, понятном компьютеру с абсолютно точной и однозначной записью команд.
Таким образом, алгоритм должен быть записан на каком-то промежуточном языке, с точными и однозначными правилами и отличном от естественного языка и языка блок-схем, но понятном компьютеру. Такой язык принято называть языком программирования.
Программный способ записи алгоритма – это запись алгоритма на языке программирования, позволяющем на основе строго определенных правил формировать последовательность предписаний, однозначно отражающих смысл и содержание алгоритма, с целью его последующего исполнения на компьютере.
Запись алгоритма на языке программирования называется компьютерной программой.
Источник
Способы описания алгоритмов



Правила оформления схем алгоритмов
Условные обозначения и правила выполнения схем алгоритмов регламентируются требованиями Единой системы программной документации в соответствии с ГОСТ 19.701-90 [6].
Схема алгоритма состоит из символов, краткого пояснительного текста и соединяющих линий (см. Приложение). Символы предназначены для графического обозначения отдельных операций, суть которых выражается текстом внутри символов. Символы должны быть по возможности одного размера и располагаться в схеме равномерно, в любой ориентации, но предпочтительным является их горизонтальное расположение.
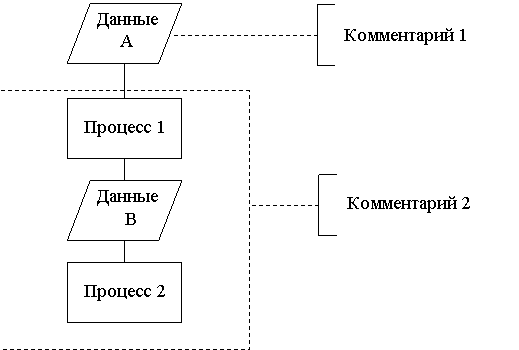
Внутри символа помещается минимальное количество текста, необходимого для понимания функции данного символа. Если такой текст требует значительного увеличения размера символа, то для размещения текста следует использовать символ «комментарий». Пунктирная линия символа «комментарий» связывается с соответствующим символом или может обводить группу символов (рис. 2).
Рис. 2.
Символы в схеме соединяются линиями, которые указывают потоки управления. Направление потока слева направо и сверху вниз считается стандартным. Направление потока, отличное от стандартного, должно быть отмечено стрелкой на конце линии (при вхождении потока в символ или в другую линию потока). Линии должны быть направлены к центру символа. Следует избегать пересечения линий, если потоки в данном месте не входят друг в друга. При необходимости линии в схемах следует разрывать во избежание лишних пересечений или слишком длинных линий, а также, если схема состоит из нескольких страниц. Соединитель в начале разрыва является внешним, а в конце разрыва — внутренним. В комментариях к соединителям могут быть приведены ссылки к страницам (рис.3).
Рис. 3.
Как правило, каждый символ имеет один вход и один выход. Исключение составляют символы:
- «терминатор» (у операции «начало» нет входа, у операции «конец» нет выхода),
- «решение» (один вход и несколько выходов),
- «подготовка» (организация цикла, пример см. на с.33).
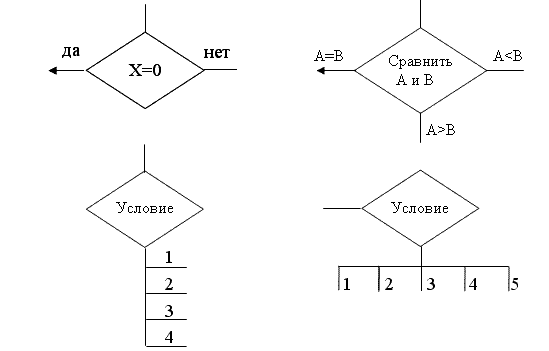
Символ «решение» является логическим. Каждый выход из символа «решение» должен сопровождаться значением условия, приведенного внутри (рис.4).
Рис. 4
Представление алгоритма решения задачи в виде схемы является наиболее наглядным, позволяет проследить процесс прохождения данных, связи между отдельными участками программы. Однако, схема должна быть удобочитаемой, т.е. не должна быть чересчур мелкой, подробной, «перегруженной», чтобы не потерять своей наглядности.
В случае описания решения очень большой, сложной задачи рекомендуется выполнять схему с несколькими уровнями детализации, число которых зависит от размеров и сложности задачи. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом. При этом весь алгоритм разбивается на смысловые фрагменты, связь между которыми следует указать на более крупной схеме. Сами же фрагменты удобнее выполнять на отдельных страницах, желательно каждый фрагмент размещать на одной странице, не перегружая чрезмерно ссылками и комментариями.
Способы описания алгоритмов
Существуют следующие способы описания (представления) алгоритмов:
1. словесное описание;
2. описание алгоритма с помощью математических формул;
3. графическое описание алгоритма в виде блок-схемы;
4. описание алгоритма с помощью псевдокода;
5. комбинированный способ изображения алгоритма с использованием словесного, графического и др. способов.
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться.
Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.
Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.

Символы, из которых состоит блок-схема алгоритма, определяет ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно.
Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.
Рассмотрим простейший пример. Пусть необходимо описать алгоритм вывода на экран монитора наибольшего значения из двух чисел.
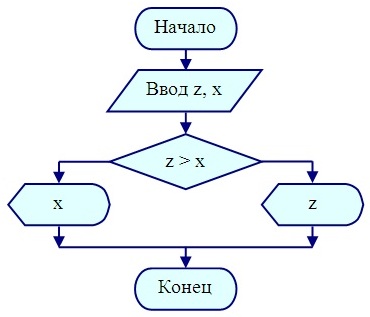
Рисунок 1 — Пример описания алгоритма в виде блок-схемы
Описание этого же алгоритма на псевдокоде:
2. Ввод чисел: Z, X
3. Если Z > X то Вывод Z
4. Иначе вывод Х
Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.
Источник