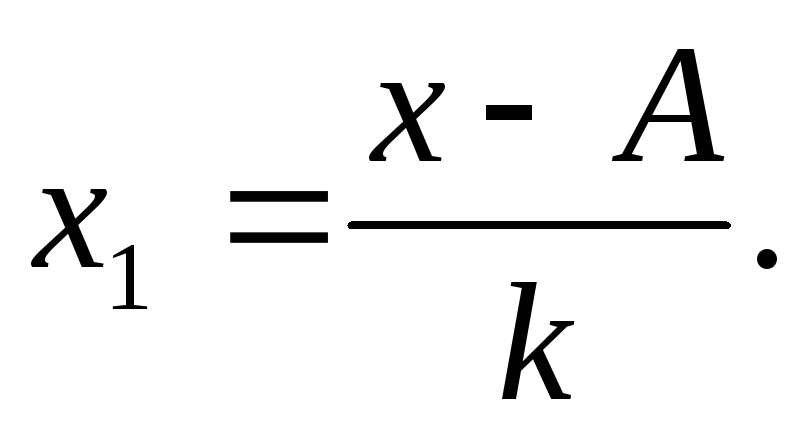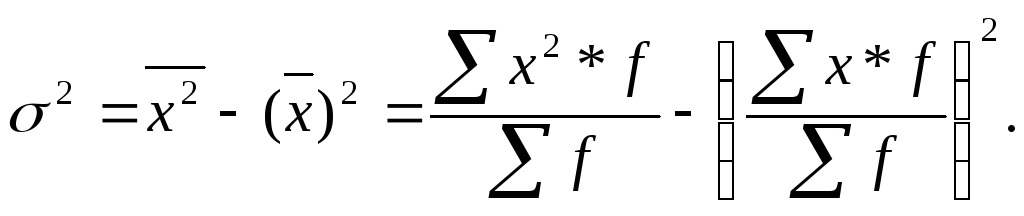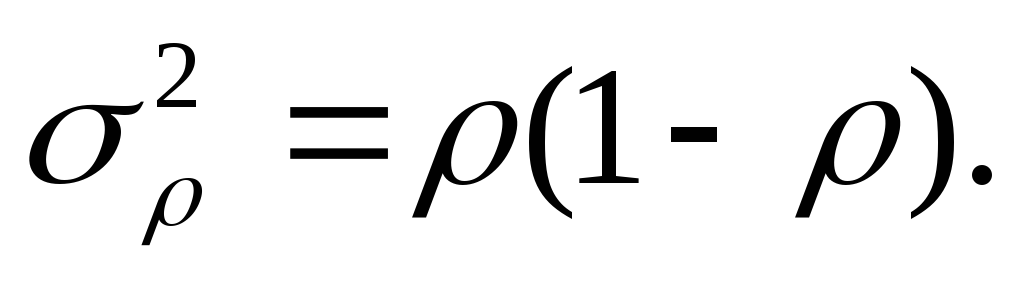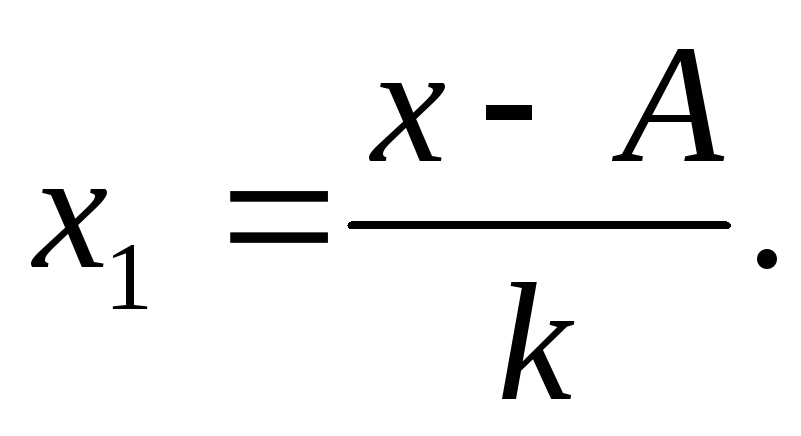Укажите способы расчета дисперсии

Как найти дисперсию?

Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $\sigma(X)=\sqrt$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле: $$ D(X)=M(X-M(X))^2, $$ которую также часто записывают в более удобном для расчетов виде: $$ D(X)=M(X^2)-(M(X))^2. $$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид: $$ D(X)=\sum_^-\left(\sum_^ \right)^2. $$ Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx — \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения: $$ x_i \quad 1 \quad 2 \\ p_i \quad 0.5 \quad 0.5 $$ и $$ y_i \quad -10 \quad 10 \\ p_i \quad 0.5 \quad 0.5 $$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии: $$ D(X)=\sum_^-\left(\sum_^ \right)^2 =\\ = 1^2\cdot 0.5 + 2^2 \cdot 0.5 — (1\cdot 0.5 + 2\cdot 0.5)^2=2.5-1.5^2=0.25. $$ $$ D(Y)=\sum_^-\left(\sum_^ \right)^2 =\\ = (-10)^2\cdot 0.5 + 10^2 \cdot 0.5 — (-10\cdot 0.5 + 10\cdot 0.5)^2=100-0^2=100. $$ Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $\sigma(X)=0.5$, $\sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения: $$ x_i \quad -1 \quad 2 \quad 5 \quad 10 \quad 20 \\ p_i \quad 0.1 \quad 0.2 \quad 0.3 \quad 0.3 \quad 0.1 $$

Снова используем формулу для дисперсии дискретной случайной величины: $$ D(X)=M(X^2)-(M(X))^2. $$ В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание: $$ M(X)=\sum_^ =-1\cdot 0.1 + 2 \cdot 0.2 +5\cdot 0.3 +10\cdot 0.3+20\cdot 0.1=6.8. $$ Потом математическое ожидание квадрата случайной величины: $$ M(X^2)=\sum_^ = (-1)^2\cdot 0.1 + 2^2 \cdot 0.2 +5^2\cdot 0.3 +10^2\cdot 0.3+20^2\cdot 0.1=78.4. $$ А потом подставим все в формулу для дисперсии: $$ D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16. $$ Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x \in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины: $$ D(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx — \left( \int_<-\infty>^ <+\infty>f(x) \cdot x dx \right)^2. $$ Вычислим сначала математическое ожидание: $$ M(X)=\int_<-\infty>^ <+\infty>f(x) \cdot x dx = \int_<0>^ <6>\frac <18>\cdot x dx = \int_<0>^ <6>\frac <18>dx = \left.\frac <54>\right|_0^6=\frac<6^3> <54>= 4. $$ Теперь вычислим $$ M(X^2)=\int_<-\infty>^ <+\infty>f(x) \cdot x^2 dx = \int_<0>^ <6>\frac <18>\cdot x^2 dx = \int_<0>^ <6>\frac <18>dx = \left.\frac <72>\right|_0^6=\frac<6^4> <72>= 18. $$ Подставляем: $$ D(X)=M(X^2)-(M(X))^2=18-4^2=2. $$ Дисперсия равна 2.

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку «Вычислить».
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Способы расчета дисперсии. Виды дисперсий, их взаимосвязь

Дисперсия обладает рядом свойств (доказываемых в математической статистике), которые позволяют упростить расчеты.

1 способ. Дисперсия определяется как разность между средней квадратов вариантов и квадратом их средней:

(5.13)

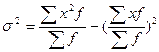
2 способ. Способ отсчета от условного нуля или способ моментов. Используется при условии равных интервалов.

(5.14)

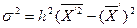
Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком (р), и доли единиц, не обладающих им(q) :

(5.15)

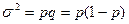
Изучая дисперсию признака в пределах изучаемой совокупности мы не можем определить влияние отдельных (случайных) факторов, характеризующих колеблемость индивидуальных значений признака. Это можно сделать при помощи группировок, разделив изучаемую совокупность на группы, однородные по признаку – фактору. При этом определяется три показателя вариации признака в совокупности:

общая дисперсия, межгрупповая дисперсия и средняя из внутригрупповых дисперсий.

Общая дисперсия характеризует вариацию признака, которая зависит от всех факторов. Она определяется по формуле:

. (5.16)

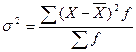
Межгрупповая дисперсия отражает вариацию изучаемого признака под влиянием признака – фактора, положенного в основу группировки. Она характеризует колеблемость групповых средних около общей средней:

(5.17)

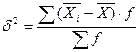
Средняя из внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием случайных, не учтенных факторов и не зависит от фактора, положенного в основу группировки:

(5.18)

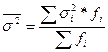
Между этими дисперсиями существует соотношение, определяемое правилом сложения дисперсий. Согласно этому правилу, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

(5.19)

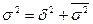
Это правило имеет большую практическую значимость, т.к. позволяет выявить зависимость результатов от определяющих факторов.

Отношение межгрупповой дисперсии к общей позволяет судить о связи между изучаемыми признаками и называется коэффициентом детерминации():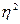

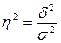
(5.20)

Источник

4.4. Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.

Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.

Первое свойство заключается в том, что если из всех вариант вычесть какое-то постоянное число, то дисперсия от этого не изменится. Оно позволяет рассчитывать дисперсию не по отклонениям вариант от средней (часто имеющей дробное значение), а по отклонениям от целого числа. Второе свойство позволяет все варианты разделить на какое-то постоянное число, например на значение интервала, и исчислить дисперсию уменьшенных вариант, а полученную величину умножить на квадрат этого числа.

, .

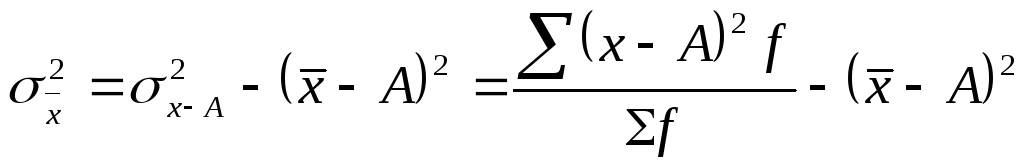
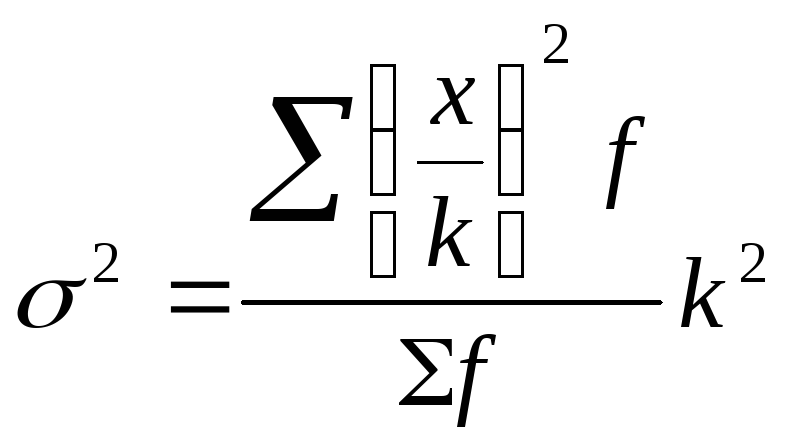
где:  2 _x – дисперсия отклонений вариантов от средней арифметической;

–дисперсия отклонений вариантов от произвольной величины А.

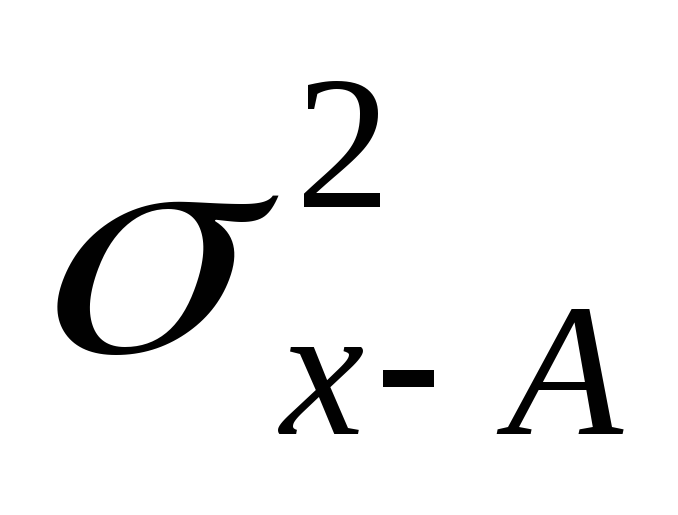
1. На этих свойствах основан расчет дисперсии способом отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х₁=(х – А)/k, и последующем расчете дисперсии по формуле:

способ отсчета от условного нуля: ;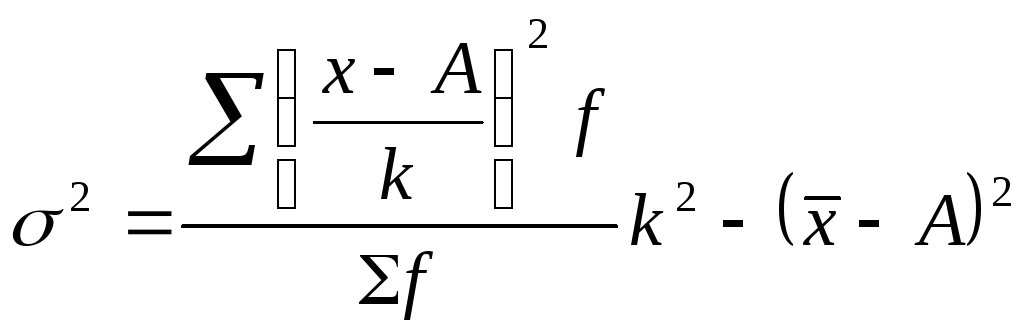

способ моментов: 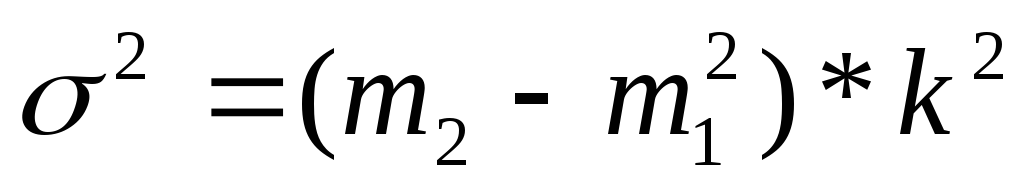, где

условный момент первого порядка: ;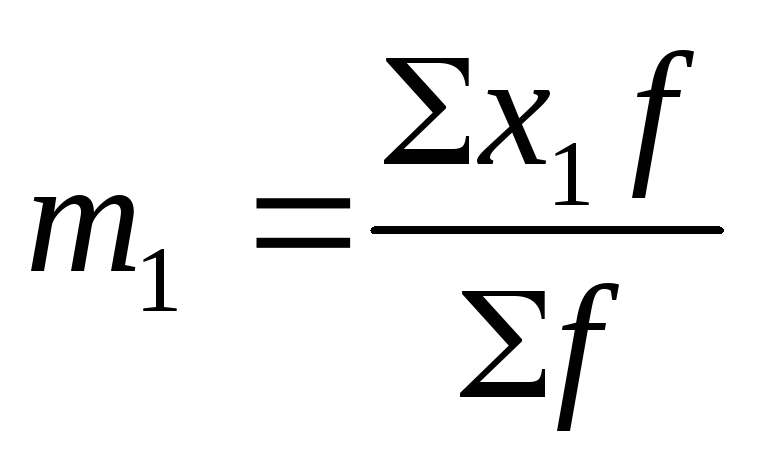

условный момент второго порядка: ,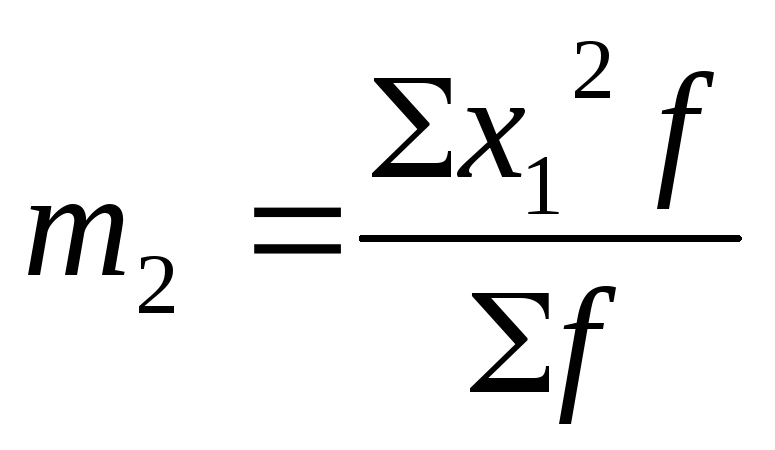

2. Дисперсия равна среднему квадрату значений признака за вычетом квадрата среднего значения признака:

Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.

В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком. Например, доля междугородных телефонных соединений (разговоров), предоставленных с ожиданием до 1 часа. Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака. Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда

Естественно, средняя постоянная величины р есть сама эта величина, а дисперсия равна:

Средняя и дисперсия это частные случаи более широкого понятия обобщающих характеристик любого распределения моментов.

Момент распределения – это средняя арифметическая тех или иных степеней отклонений вариантов х от некоторой постоянной величины А:

_z = .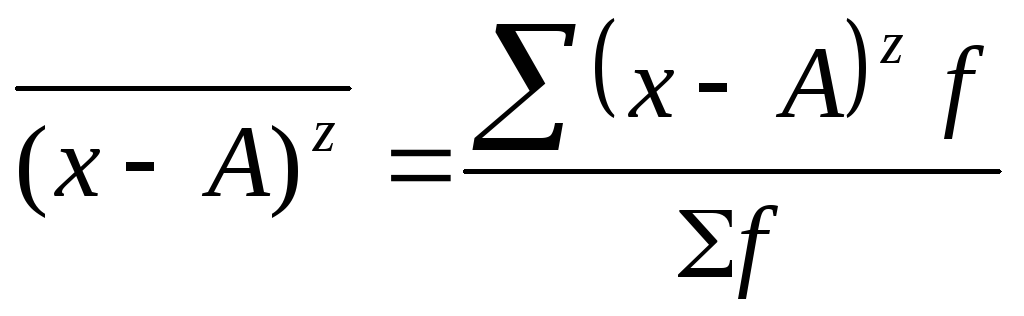

Порядок момента определяется величиной z, т.е. степенью, в которую возводится отклонение вариант. В зависимости от принятой величины А различают три вида моментов:

начальные (при А=0): ; центральные (при А=): ;

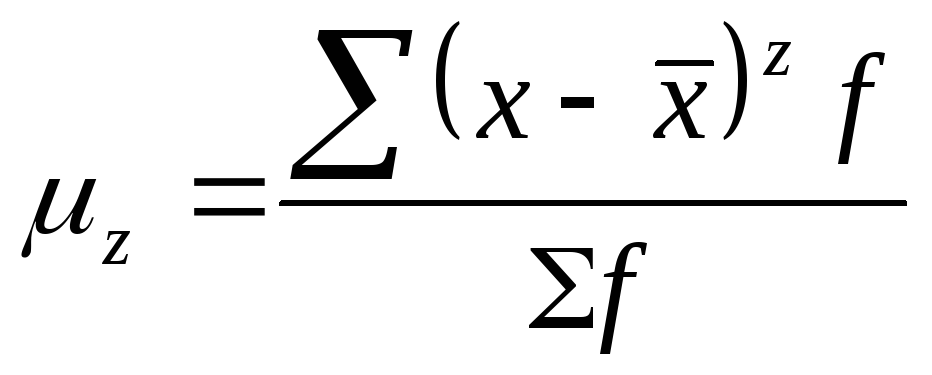
условные (при А≠0, А≠): .

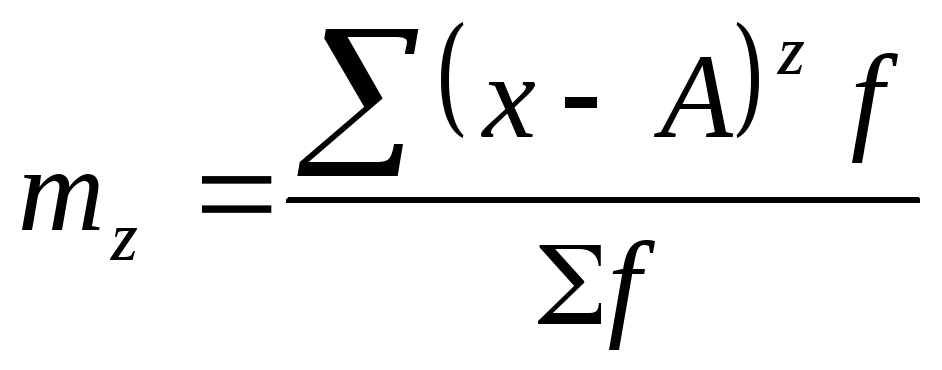
Начальный момент первого порядка представляет собой среднюю арифметическую: ;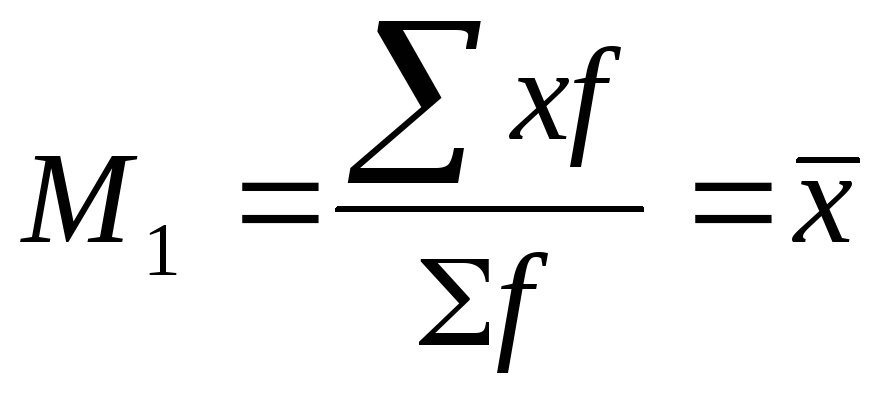

центральный момент второго порядка – дисперсию: 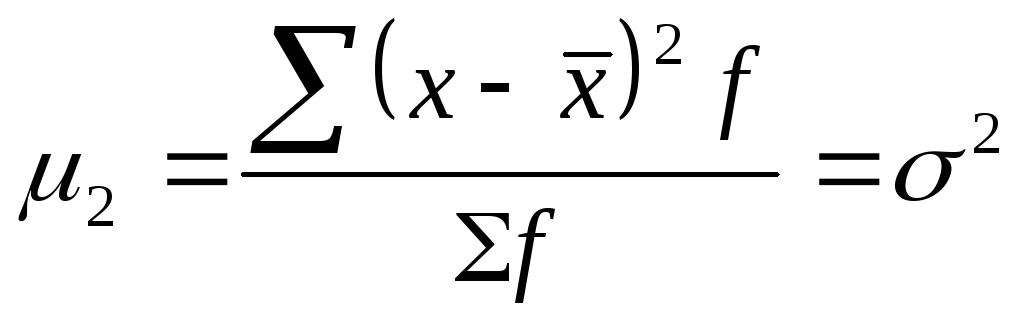. Центральный момент первого порядка ₁ всегда равен нулю (сумма отклонений вариант от средней равна нулю); центральный момент третьего порядка равен нулю в симметричном распределении.

Условные моменты самостоятельного значения не имеют, ими пользуются для упрощения вычисления центральных моментов: ₂ = m₂ – m 2 ₁; ₃ = m₃ – 3m₁ m₂ + 2m 3 ₁; ₄ = m₄ – 4m₃ m₁ + 6m₂ m 2 ₁ – 3 m 4 ₁.

Для исчисления условных моментов используется условная величина:

; ; ; ; где

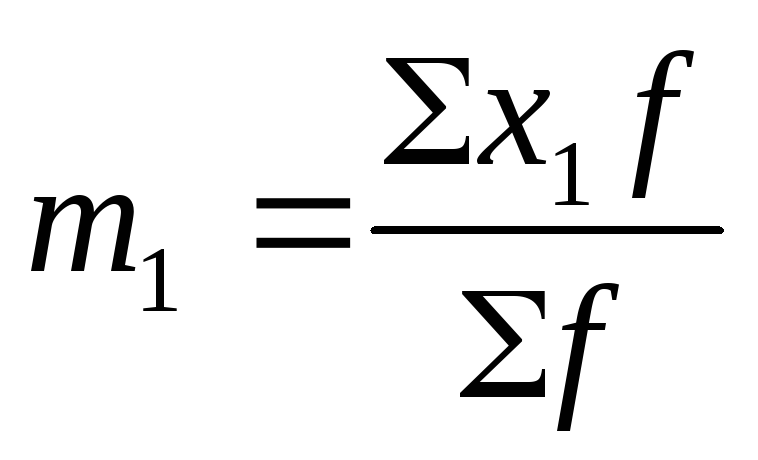
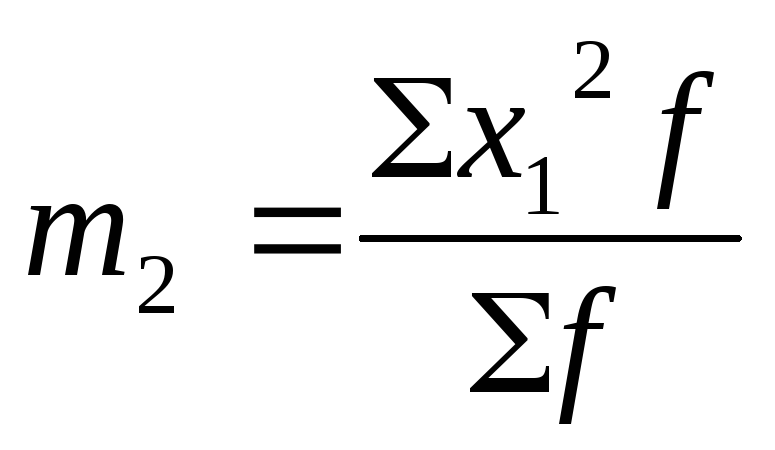
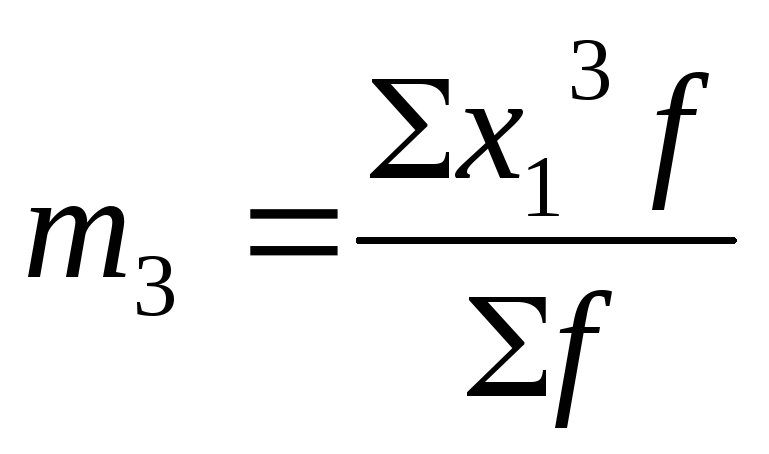
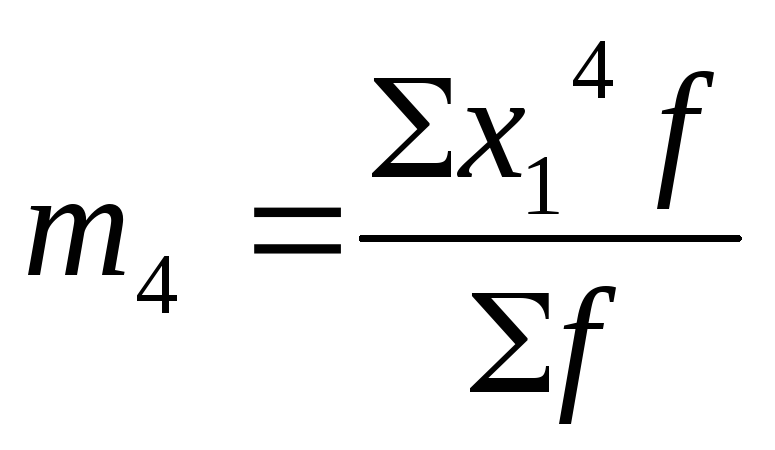
В этом случае центральные моменты корректируются на величину k z :

Наряду с изучением вариации признака по всей совокупности в целом часто возникает необходимость проследить количественные изменения признака по группам, на которые разбита вся совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

.

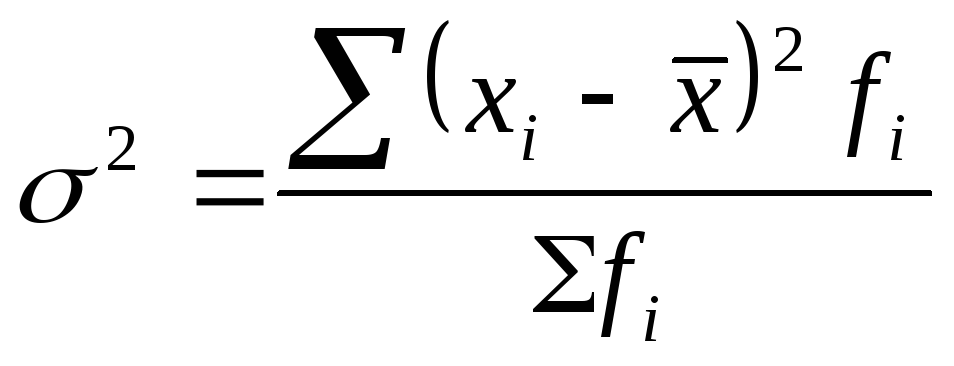
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:

, где

— соответственно средние и численности по отдельным группам,

— средняя всей совокупности.

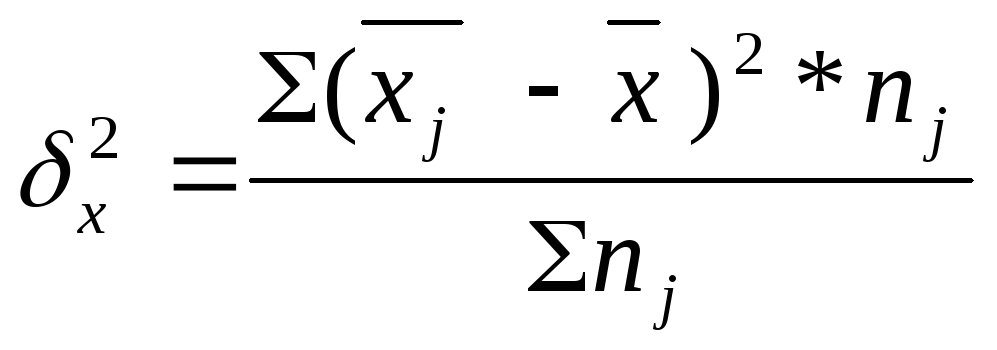
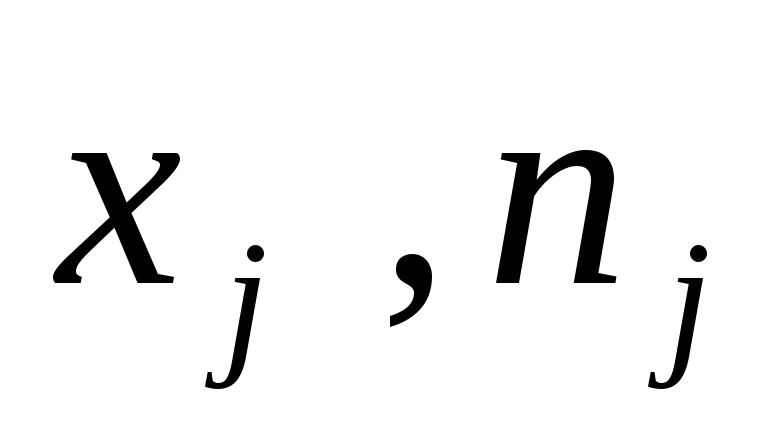
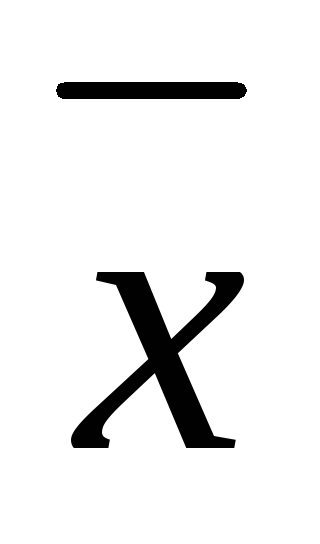
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:

, где

— варианты групп, — численность группы,— средняя группы

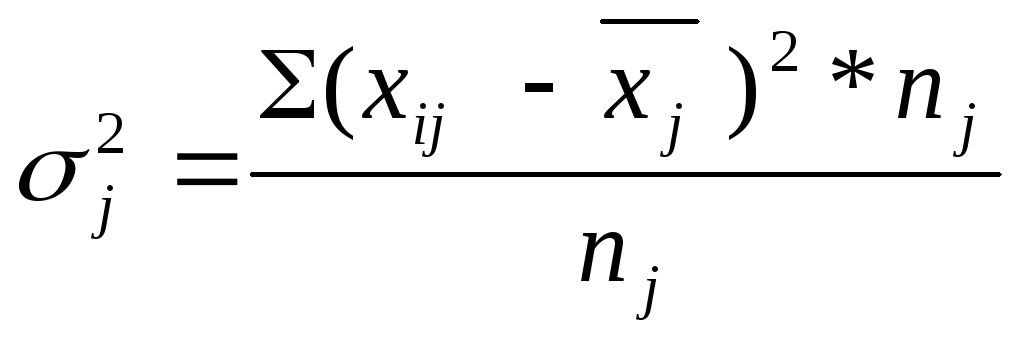
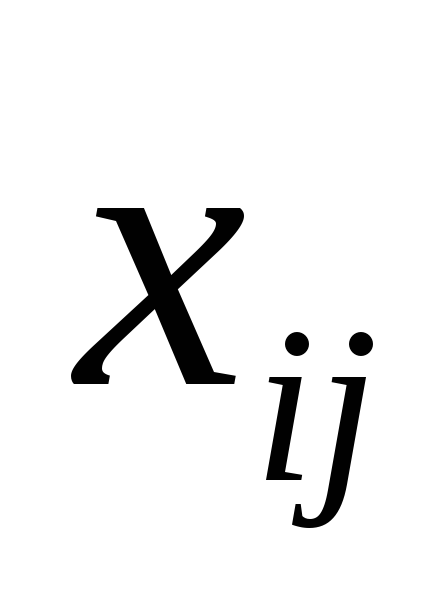
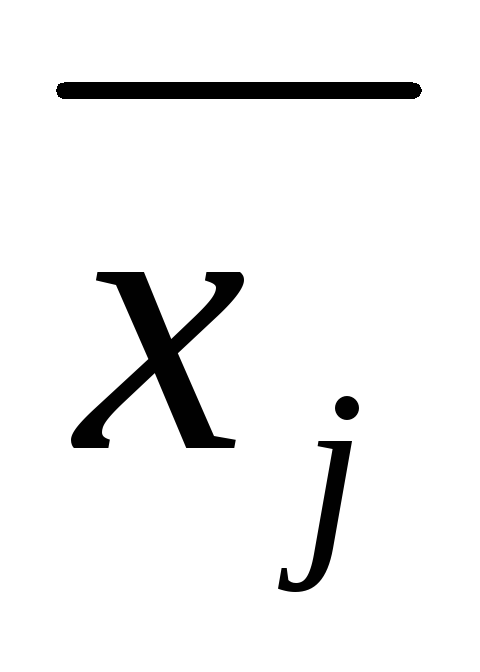
Средняя из внутригрупповых дисперсий определяется по формуле:

.

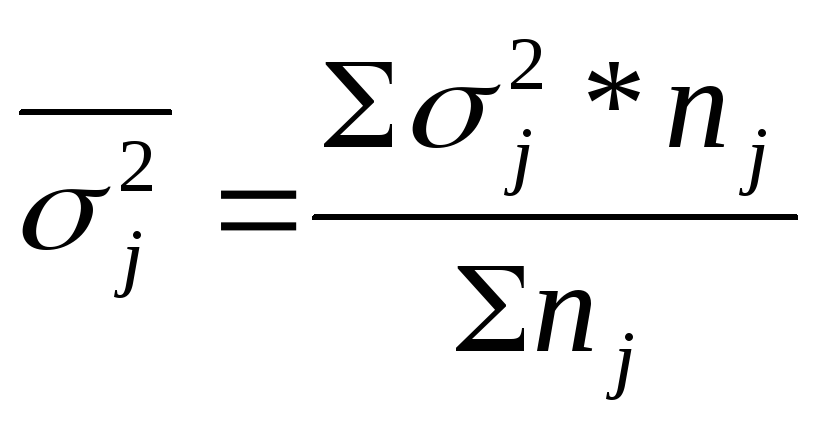
Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

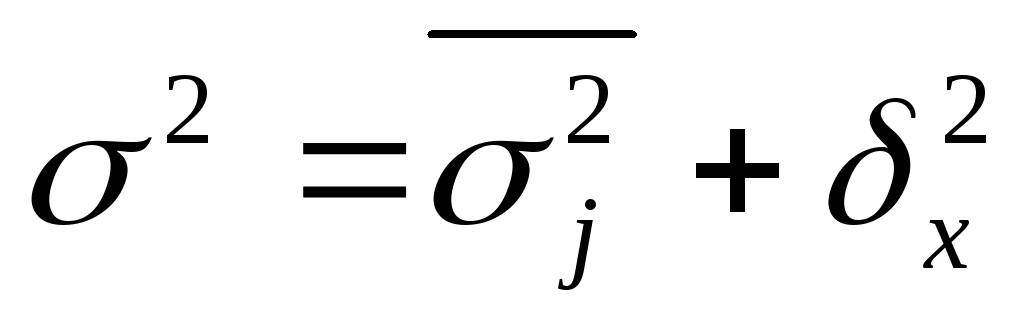
Данная сумма называется правилом сложения дисперсий.

Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результирующим признаками. Он называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:

.

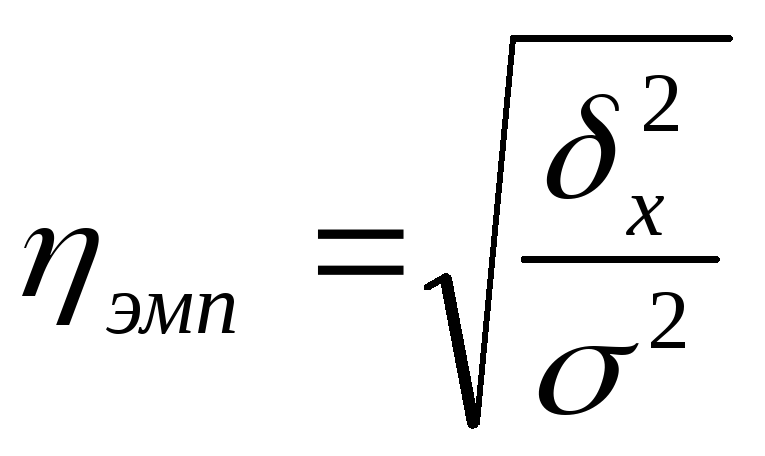
Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминации и показывает долю группировочного признака в общей вариации:

.

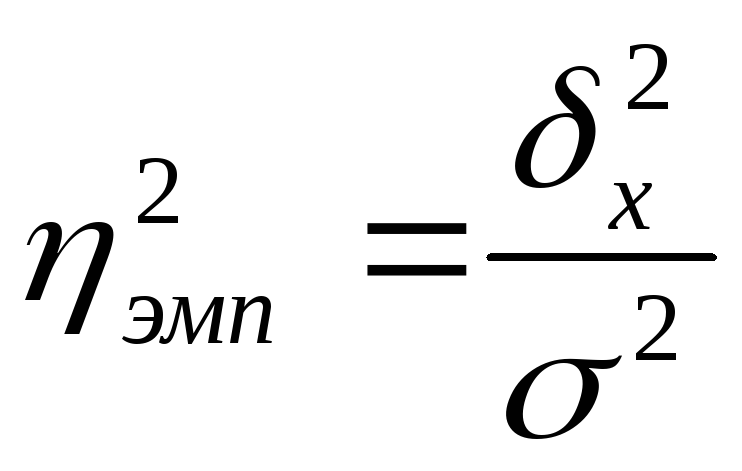
Источник