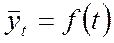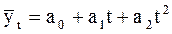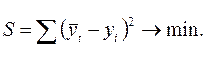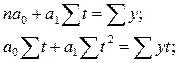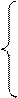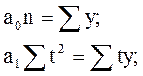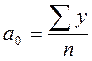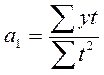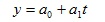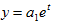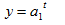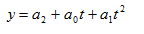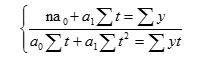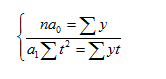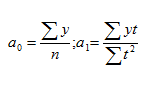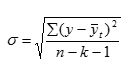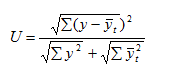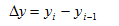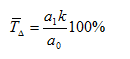Укажите способы изучения основных тенденций динамического ряда

Методы анализа основной тенденции развития в рядах динамики

Важной задачей статистики является определение в рядах динамики общей тенденции развития явления.

Иногда закономерность изменения явления, общая тенденция его развития отчетливо отражается уровнями динамического ряда (уровни на изучаемом периоде непрерывно растут или непрерывно снижаются).

Однако часто приходится встречаться с такими рядами ди­намики, в которых уровни ряда постоянно изменяются (то возрастают, то убывают), и общая тенденция неясна.

На развитие явления во времени оказывают влияние факто­ры, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.

Поэтому при анализе динамики речь идет не просто о тен­денции развития, а об основной тенденции.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различ­ных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения ин­тервалов, скользящей средней и аналитического выравнивания.

Одним из наиболее простых методов изучения основной тенденции в рядах динамики являетсяукрупнение интервалов. Он основан на укрупнении периодов времени, к которым отно­сятся уровни ряда динамики (одновременно уменьшается коли­чество интервалов). Например, ряд ежесуточного выпуска про­дукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Выявление основной тенденции может осуществляться такжеметодом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из опреде­ленного числа, обычно нечетного (3, 5, 7 и т.д.), первых по сче­ту уровней ряда, затем — из такого же числа уровней, но начи­ная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, пере­двигаясь на один срок.

Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следователь­но, потеря информации.

Рассмотренные приемы дают воз­можность определить общую тенденцию развития явле­ния, более или менее освобожденную от случайных и волнооб­разных колебаний. Однако получить обобщенную статистиче­скую модель тренда нельзя.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во вре­мени, используется аналитическое выравнивание ряда динамики.

Основным содержаниемметода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени:

где 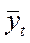— уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней 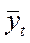произ­водится на основе адекватной математической модели, которая отображает (аппроксимиру­ет) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Простейшими моделями (формулами), выражаю­щими тенденцию развития, являются:

линейная функция — прямая 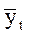= а₀ + a₁t,

где а₀ и а₁ — параметры уравнения;

показательная функция- ,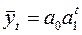

степенная функция — кривая второго порядка (парабола)

В тех случаях, когда требуется особо точное изучение тен­денции развития (например, модели тренда для прогнозирова­ния), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Расчет параметров функции производится методом наименьших квадратов, в котором в качестве решения принима­ется точка минимума суммы квадратов отклонений между тео­ретическими и эмпиричесими уровнями:

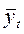
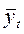
где — выравненные (расчетные) уровни; у_i — фактические уровни. Параметры уравнения а_i удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выравненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у_i изменяю­щимися уровнями , наилучшим образом аппроксимирующи­ми статистические данные.

• Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически посто­янны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

• Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометриче­ской прогрессии, т. е. когда цепные коэффициенты рос­та практически постоянны.

Рассмотрим «технику» выравнивания ряда динамики по пря­мой:

= а₀ + a₁t,

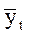
Параметры а₀ и а₁ согласно методу наимень­ших квадратов находятся решением следующей системы нор­мальных уравнений, полученной путем алгебраического преобра­зования условия:

где у — фактические (эмпирические) уровни ряда; t — время (по­рядковый номер периода или момента времени).

Расчет параметров упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент).

При четном числе уровней (например, 4), значения t — ус­ловного обозначения времени будут такими (это равнозначно из­мерению времени не в годах, а в полугодиях):.

1996г. 1997г. 1998г. 1999г.

При нечетном числе уровней (например, 5) значения уста­навливаются по-другому:

1996 г 1997г. 1998г. 1999г. 2000г.

В обоих случаях Σ t = 0, так что система нормальных урав­нений принимает вид:

Из первого уравнения

Из второго уравнения

Источник

Динамические ряды — краткое руководство по анализу изменений явлений во времени

Даная статья понятными и простыми терминами объяснит, что же такое динамические ряды, для чего они нужны, как производится анализ полученных данных и какие возможности открываются перед теми, кто владеет методикой данного анализа. Любое явление в области здравоохранения нуждается в тщательной оценке, и здесь знания анализа динамических рядов неоценимы. С помощью динамического ряда можно оценить и спрогнозировать проблематику любой нозологической единицы, сформировать дальнейшую тактику лечения и меры профилактики заболеваний.

Динамический ряд — ряд однородных величин, характеризующих изменение явления во времени.

Целью анализа динамических рядов является:

• выявление закономерности изменения изучаемого явления во времени;
• прогнозирование (экстраполирование) полученных данных на последующие
  годы.

Числовые значения, составляющие динамический ряд, называются уровнями ряда (у).

Типы динамических рядов:

1. В зависимости от вида уровня ряда:

а) простые (уровень ряда выражен абсолютными числами);

б) сложные (уровень ряда выражен обобщающими коэффициентами).

1. В зависимости от способа формирования временного интервала:

а) моментные (данные собираются на определенный момент времени);

б) интервальные (данные собираются за определенный период времени).

1. В зависимости от выраженности изменений явления во времени (определя­ется по коэффициенту корреляции между временем и изучаемым явлением).

а) с выраженной тенденцией (r =0,7 — 1,0);

б) с неустойчивой тенденцией (r =0,3 — 0,69);

в) с отсутствием тенденции ( r = 0 — 0,29).

Основное требование, предъявляемое к анализируемым динамическим ря­дам, заключается в сопоставимости их уровней. Для оценки сопоставимости прово­дят предварительный анализ полученных данных по следующим критериям:

• единство территории, на которой проводился сбор данных;
• единая методология учета данных;
• единые временные интервалы, в течение которых проводилась регистрация
  данных.

Методика анализа динамических рядов

Методика аналитики предусматривает выполнение последовательных действий:

1. Представить полученные данные графически и выявить форму зависимости изучаемого явления от времени.
2. Оценить наличие и силу корреляции изучаемого явления от времени.
3. Если установлено, что ряд обладает выраженной тенденцией, проводят анализ компонентов динамики ряда: основной тенденции (эволюции, тренда), кратковременных систематических движений и случайных колебаний. Основная задача анализа — разделить эти компоненты и выявить основную закономерность изменения явления во времени. Для выявления и описания тренда динамический ряд подвергают обработке — выравниванию.

Способы выравнивания динамических рядов

Чтобы произвести выравнивание динамических рядов потребуются следующие действия:

• Укрупнение временных интервалов (периодов), в течение которых изучается явление.
• Сглаживание ряда методом скользящей средней.
• Аналитический способ.

При этом способе на основании фактических данных подбирается наиболее подходящее для отражения тенденции развития явления математическое уравнение (аппроксимирующая функция), которое принимается за модель развития явления во времени. Т.е. уровни ряда рассматриваются как функция времени, и задача выравнивания сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету по найденной формуле теоретических выравненных уровней. Наиболее часто используются следующие функции:

а) линейная зависимость:

б) экспоненциальная зависимость:

в) показательная зависимость:

г) параболическая зависимость:

у – теоретический уровень;

t – временной интервал.

В качестве примера возьмем линейную зависимость и проведем выравнивание, используя для нахождения параметров уравнения а₀ ,а₁ способ наименьших квадратов. Способ наименьших квадратов позволяет найти теоретическую кривую, максимально приближенную к эмпирической, а условие минимума суммы квадратов отклонений теоретических данных от фактических позволяет свести математическое решение задачи к системе нормальных уравнений:

где у — уровни фактического ряда;

n — количество уровней;

t — порядковый номер временного периода.

Эта система уравнений легко упрощается, если «t» присвоить ранги (порядковые номера), ведя отсчет времени от середины ряда. При нечетном ряде середина обозначается через 0, а отсчет рангов ведется через единицу с соответствующим знаком в ту или иную сторону от середины (например: -5,-4,-3,-2,-1, 0,+1.+2,+3,->:4,+5). При четном ряде две средние временные точки обозначаются через +1 и -1, а остальные ранги присваиваются через две единицы (например: -5,-3,-1,+1,+3,+5).

При отсчете времени от середины ряда St = 0 и система нормальных уравнений принимает вид:

Отсюда находим параметры уравнения:

Подставляя в уравнение у = а₀ + а₁t вместо «t» его ранги, находим выравненные (теоретические) значения уровней ряда и строим теоретическую кривую выравненного динамического ряда.

При использовании аналитического способа всегда отмечается отклонение теоретических уровней от фактических уровней ряда, которое может быть обуслов­лено как случайными колебаниями, так и неправильно подобранным аппроксими­рующим уравнением. В связи с этим заключительным этапом выравнивания динамического ряда аналитическим способом является оценка точности аппроксимации с определенным уровнем значимости.

Оценка точности аппроксимации возможна с помощью нахождения

Для получения точной оценки необходимо найти такие величины:

а) коэффициент вариации:

где у- фактический уровень ряда;

y_t — теоретический уровень ряда;

k- число параметров уравнения;

n- число уровней ряда.

Аппроксимация считается точной при C_v не более 15%.

б) коэффициент расхождения Тейла:

где у — фактический уровень ряда;

y_t — теоретический уровень ряда.

Аппроксимация считается точной при U не более 5%

После аналитического выравнивания динамического ряда и описания тренда возможно экстраполировать полученные данные. Экстраполяция — предположение о сохранении тренда, базирующееся на допущении неизменности влияющих факто­ров и предшествующей тенденции. Осуществляется путем подставления в найденное уравнение аппроксимации не фактического значения временного интервала, а предполагаемого порядкового номера (ранг) того периода, на который прогнозируется результат.

Вычисление основных показателей динамического ряда

Алгоритм вычислений ведущих параметров динамических рядов:

yi- текущий уровень (сравниваемый);

у_i-1— базисный уровень (с каким сравнивают);

t- период времени, в течение которого уровень предполагается неизменным.

1.Абсолютный прирост (убыль) :

2.Темп роста (убыли):

3.Темп прироста (относительная скорость), темп убыли :

4.Средний темп прироста (убыли):

где а₀; а₁ — параметры уравнения;

k = 1 при нечетном ряде;

k = 2 при четном ряде.

5.1% прироста (убыли): используются при сравнении динамических рядов с уровнями, выраженными различными обобщающими коэффициентами.

Таким образом, с помощью данного руководства по определению и расчетам такого понятия, как, динамические ряды, специалисты различных отраслей медицины, ученые могут эффективно и быстро оценить изменение различных величин в течение времени.

Благодарим за интерес, проявленный к нашей статье, оставайтесь с нами!

Источник