Укажите количество различных способов сформировать команду

Задачи по комбинаторики для 11 класса

Подборка задач по комбинаторике (с ответами) для 11 класса.

Просмотр содержимого документа
«Задачи по комбинаторики для 11 класса»

Задачи по комбинаторики

Задача 1: Сколькими способами можно составить список из 5 учеников?

Ответ: перестановки, 5! = 120.

Задача 2: В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Ответ: размещения из 11 по 2, А 2 ₁₁= 110.

Задача 3: Расписание на день содержит 5 уроков. Определить количество возможных расписаний при выборе из 14 предметов, при условии, что ни один предмет не стоит дважды.

Ответ: размещения из 14 по 5, 1320.

Задача 4: Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета?

Ответ: перестановки, 6 способов.

Задача 5: В классе 24 ученика. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?

Ответ: сочетания из 24 по 4,

Задача 6: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 6 способов.

Задача 7: Сколькими различными способами можно избрать из 15 человек делегацию в составе 3 человек?

Ответ: сочетания, 455 способами.

Задача 8: Из ящика, где находится 15 шаров, нумерованных последовательно от 1 до 15, требуется вынуть 3 шара. Определить число возможных комбинаций при этом?

Ответ: размещения, 2830 способами.

Задача 9: Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра входит в изображение числа только 1 раз?

Ответ: перестановки, 4! – 3! =18.

Задача 10: Сколькими способами можно разместить 6 пассажиров в четырехместной каюте?

Ответ: размещения из 6 элементов по 4, 360 способами.

Задача 11: Сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?

Ответ: сочетания из 10 элементов по 2, 45 способами.

Задача 12: Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек?

Ответ: сочетания из 13 по 4, 715 бригад.

Задача 13: При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Ответ: сочетания из 16 по 2, 120 рукопожатий.

Задача 14: Группа учащихся в 30 человек пожелала обменяться своими фотокарточками. Сколько всего фотокарточек потребовалось для этого?

Ответ: сочетание из 30 по 2, 435 фотокарточек.

Задача 15: Сколько различных плоскостей можно провести через 10 точек, если никакие три из них не лежат на одной прямой и никакие четыре точки не лежат в одной плоскости?

Ответ: сочетание из 10 по 3; 120 точек

Задача 16: Сколько существует различных семизначных телефонных номеров?

Задача 17: Сколько существует различных семизначных телефонных номеров, если в каждом номере нет повторяющихся цифр?

Ответ: размещение из 10 по 7.

Задача 18: Сколько существует таких перестановок 7 учеников, при которых 3 определенных ученика находятся рядом друг с другом? Ответ: 720 = 3! · 5!

Задача 19: На книжной полке стоит собрание сочинений в 30 томах. Сколькими различными способами их можно переставить, чтобы: а) тома 1 и 2 стояли рядом; б) тома 3 и 4 рядом не стояли?

Задача 20: Сколько существует трёхзначных чисел, все цифры которых нечётные и различные?

Ответ: размещение из 5 по 3, 60.

Задача 21: У одного мальчика имеется 10 марок для обмена, а у другого – 8. Сколькими способами они могут обменять 2 марки одного на 2 марки другого?

Ответ: сочетания, С 2 ₁₀·С 2 ₈ = 1260.

Источник

СРОЧНО. В 9А классе учится 25 человек, а в 9Б-28 человек. Сколько существует способов сформировать команду из 10 ч.

Сначала поймём, сколько способов есть выбрать 5 человек из 9А.
Первым мы можем взять любого из 25, вторым — любого из 24 оставшихся, третьим — любого из 23, четвёртым — любого из 22, пятым — любого из 21.
То есть количество способов выбрать 5 человек из 9А класса равно 25*24*23*22*21.
Но тут есть проблема. Каждую команду мы считаем больше одного раза. Нам ведь важно только то, кто попал в команду, а кто нет — неважно, на каком шаге мы ученика отобрали. Например, если Антона выбрать первым, Бориса — вторым, Веру — третьей, Галину — четвёртой и Дарью — пятой, то будет та же самая команда, как если бы мы их выбрали в порядке Дарья-Галина-Антон-Борис-Вера или в порядке Антон-Вера-Борис-Дарья-Галина, или ещё в каком-то.
В команде 5 человек. Всего существует ровно 5*4*3*2*1 способов выбрать именно эту команду: любой человек может быть выбран первым, любой из оставшихся — вторым и так далее.

С учётом этого количество способов, которым можно выбрать команду в 5 человек из 9А, равно
25*24*23*22*21 / 5*4*3*2
Это количество имеет своё обозначение. «Число сочетаний из 25 по 5», C(25,5). Оно равно 53130

Аналогично, из 9Б можно выбрать 5 человек
28*27*26*24*25 / 5*4*3*2 способами.

Это C(28,5). Оно равно 98280.

Общее количество способов — произведение этих чисел. Мы же можем выбрать любую команду из 9А, и в пару к ней — любую же команду из 9Б. То есть на каждую команду из 9А у нас С (28,5) вариантов команды из 9Б.

Ответ: 28*27*26*25*24*25*24*23*22*21 / (5*4*3*2)^2 = 53130 * 98280 = 5 221 616 400

Пять миллиардов двести двадцать один миллион шестьсот шестнадцать тысяч четыреста.
А всего-то — 53 человека, да 10 в команде :).

Источник

Укажите количество различных способов сформировать команду

Задача 1:

Из класса, в котором учатся 30 человек, нужно выбрать двоих школьников для участия в математической олимпиаде. Сколькими способами это можно сделать?

Решение:

Первого ученика можно выбрать 30 способами, второго, независимо от выбора первого ученика, – 29 способами. При этом каждая пара учитывается дважды. Поэтому ответ: 30 • 29/2 = 435 способов.

Задача 2:

Сколькими способами можно выбрать команду из трех школьников в классе, в котором учатся 30 человек?

Решение:

Первого ученика можно выбрать 30 способами, второго – 29 способами, третьего – 28 способами. Таким образом получаем 30 • 29 • 28 вариантов выбора. Однако каждая команда при этом подсчете учтена несколько раз: одна и та же тройка учеников может быть выбрана по разному, например, сначала А, потом В, потом С или сначала С, потом А, потом В и т.д. Поскольку число перестановок из трех элементов равно 3!, то каждая команда учтена нами ровно 3! = 6 раз. Поэтому 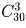равно (30 • 29 • 28)/3!.

Задача 3:

Сколькими способами можно выбрать 4 краски из имеющихся 7 различных?

Решение:

.

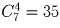
Задача 4:

У одного школьника есть 6 книг по математике, а у другого – 8. Сколькими способами они могут обменять три книги одного на три книги другого?

Решение:

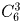
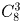
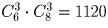
Первый школьник может выбрать 3 книги для обмена способами, второй – способами. Таким образом, число возможных обменов равно .

Задача 5:

В шахматном кружке занимаются 2 девочки и 7 мальчиков. Для участия в соревновании необходимо составить команду из четырех человек, в которую обязательно должна входить хотя бы одна девочка. Сколькими способами это можно сделать?

Решение:

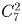
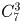
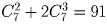
В команду входит либо одна девочка, либо две. Разберем оба случая. Если в команде две девочки, то двух мальчиков к ним можно добавить способами. Если же в команду входит только одна девочка (ее можно выбрать двумя способами), то команду можно дополнить тремя мальчиками различными способами. Таким образом, общее число возможных команд равно .

Задача 6:

Сколькими способами можно разбить 10 человек на две баскетбольные команды по 5 человек в каждой?

Решение:

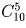
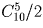
Первую команду можно выбрать способами. Этот выбор полностью определяет вторую команду. Однако при таком подсчете каждая пара команд А и В учитывается дважды: один раз, когда в качестве первой команды выбирается команда А, и второй, – когда в качестве первой команды выбирается команда В. Таким образом, ответ: .

Задача 7:

На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?

Решение:

.

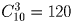
Задача 8:

Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?

Решение:

(n 8 + 1)(n 8 – 1) = n 16 – 1 = 0 (mod 17).

Задача 9:

На прямой отмечено 10 точек, а на параллельной ей прямой – 11 точек. Сколько существует а) треугольников; б) четырехугольников с вершинами в этих точках?

Решение:

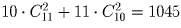
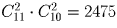
а) б) .

Задача 10:

Сколькими способами можно выбрать из 15 различных слов набор, состоящий не более чем из 5 слов?

Решение:

.

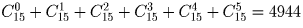
Задача 11:

Сколькими способами можно составить комиссию из 3 человек, выбирая ее членов из 4 супружеских пар, но так, чтобы члены одной семьи не входили в комиссию одновременно?

Решение:

Выберите сначала семьи, а потом в каждой паре конкретного представителя. Ответ: .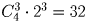

Задача 12:

В классе, в котором учатся Петя и Ваня – 31 человек. Сколькими способами можно выбрать из класса футбольную команду (11 человек) так, чтобы Петя и Ваня не входили в команду одновременно?

Решение:

Разберите три случая: в команду входит только Петя; в команду входит только Ваня; оба они в команду не входят. Ответ: .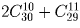

Задача 13:

Сколькими способами можно переставить буквы слова «ЭПИГРАФ» так, чтобы и гласные, и согласные шли в алфавитном порядке?

Решение:

Все определяется местами, на которых стоят гласные буквы. Ответ: .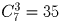

Задача 14:

Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Сколькими способами можно выбрать эту команду так, чтобы в нее вошло не более трех юношей?

Решение:

.

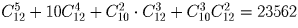
Задача 15:

Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?

Решение:

.

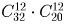
Задача 16:

а) Сколькими способами можно разбить 15 человек на три команды по 5 человек в каждой?

б) Сколькими способами можно выбрать из 15 человек две команды по 5 человек в каждой?

Решение:

а) ; б) .

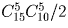
Задача 17:

Сколькими способами можно выбрать из полной колоды (52 карты) 10 карт так, чтобы

а) среди них был ровно один туз?

б) среди них был хотя бы один туз?

Решение:

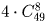
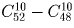
а) ; б) Перейдите к дополнению. Ответ: .

Задача 18:

Сколько существует 6-значных чисел, у которых по три четных и нечетных цифры?

Решение:

Разберите случаи в соответствии с тем, цифра какой четности стоит на первом месте. Затем в каждом случае выберите места для нечетных цифр. Ответ: .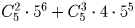

Задача 19:

Сколько существует 10-значных чисел, сумма цифр которых равна а) 2; б) 3; в) 4?

Решение:

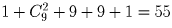
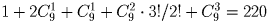
Разберите все возможные представления чисел 2, 3, 4 в виде суммы нескольких натуральных слагаемых. Не забывайте, что первая цифра – не ноль. Ответ: а) 10; б) ; в) .

Задача 20:

Человек имеет 6 друзей и в течение 5 дней приглашает к себе в гости каких-то троих из них так, чтобы компания ни разу не повторялась. Сколькими способами он может это сделать?

Решение:

.

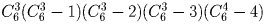
Задача 21:

Как известно, для участия в лотерее «Спортлото» нужно указать шесть номеров из имеющихся на карточке 45 номеров.

а) Сколькими способами можно заполнить карточку «Спортлото»?

б) После тиража организаторы лотереи решили подсчитать, каково число возможных вариантов заполнения карточки, при которых могло быть угадано ровно три номера. Помогите им в этом подсчете.

Решение:

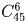
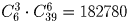
а) ; б) .

Источник