Угловое расстояние понятие единицы измерения способ определения

Угловое расстояние между звездами — онлайн расчет

При тестировании программы расчета углового расстояния между двумя точками на небесной сфере обнаружилось, что представленное здесь расчетное табло позволяет пересчитывать время из представления в часах, минутах и секундах в десятичные доли часа и наоборот, а угловые величины пересчитывает из дробно-десятичного формата в градусах в формат: градусы, минуты, секунды

Сегодня эфемериды [1] небесных светил принято представлять в экваториальных координатах [2] в формате:
прямое восхождение — чч мм сс,сс;
склонение — (°) (′) (″,″).
Именно такой формат принят за основной для распознавания в позициях строчного ввода координат небесных объектов.
В окна этих позиций вы можете внести скопированные из электронных таблиц координаты небесных объектов.
Во многих случаях будет распознана даже единая строка из двух значений координат, например, такая: 03 ч 24м 19,35c +49° 51′ 40,5″, главное, чтобы присутствовали правильные обозначения водимых угловых координат. Помимо обозначений ч — часы, м — минуты, с — секунды, программа не будет «ругаться» и на представление данных с обозначениями h — hours, m — minutes, s — seconds.
Используемая здесь программа позволяет проводить расчет «на лету», реагируя на обновление данных, но только после того как введены все необходимые значения .
Для начала расчета нужно ввести или обновить обе пары значений координат звездных объектов. Если необходимое значение координат 0,0000°, то лучше сначала в соответствующую позицию ввести ненулевое значение, а затем, после того как включился зеленый свет для расчетов снова установить 0 (можно просто добавить после нуля точку или запятую, главное, чтобы программа распознала, что все координаты введены осознанно).

Расчет углового расстояния между двумя объектами (звездами) небесной сферы

Координаты небесного
Объекта 1

Угловое расстояние между объектами

Координаты небесного
Объекта 2

Что-то пошло не так.

После того как будут введены координаты обоих объектов (планет, звезд) должен погаснуть оранжевый запрос «Данные ?», включится зеленый цвет и автоматически начнется расчет углового расстояния, если это не произошло, то кликните по зеленому полю «Расчет».

Итоговый отчет

Oбъект 1: Регул (10ч 08м 22с; 11° 58′ 12″);
Созвездие: Leo, Лев (Leo)

Oбъект 2: Спика (13ч 25м 12с; -11° 09′ 36″);
Созвездие: Vir, Дева (Virgo)

Угловое расстояние между звездами Регул и Спика: 54,06124° .

Расчет углового расстояния между двумя астрономическими объектами, положение которых определено во второй экваториальной системе координат

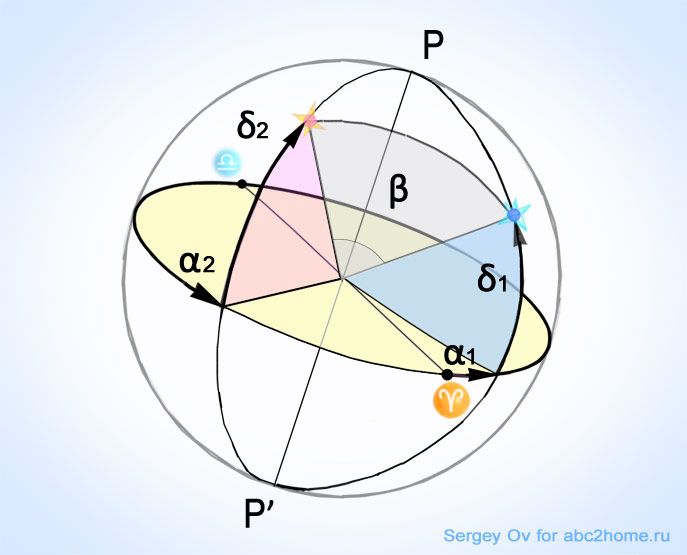
Во второй экваториальной системе координат положение объектов определяется двумя угловыми параметрами, называемыми прямое восхождение α и склонение δ (Рис.1).

Рис. 1. Небесная сфера, угловое расстояние β между двумя точками на сфере и их угловые экваториальные координаты

Как видно из рисунка, β — это угловое расстояние между двумя небесными объектами, α₁ и δ₁, прямое восхождение и склонение, характеризующие положение Объекта 1 на небесной сфере, соответственно, положение Объекта 2 характеризуется α₂ и δ₂.
Склонение определяется величиной угла от линии небесного экватора до объекта в плоскости перпендикулярной экватору. Прямое восхождение определяется величиной угла между точкой весеннего равноденствия и точкой отсчета склонения. Важно запомнить, что прямое восхождение отсчитывается от точки весеннего равноденствия в направлении противоположном движению часовой стрелки (в точке весеннего равноденствия Солнце вступает в знак Овна) и его величина выражается не градусах, а в часах. На нашем рисунке величина α₁ примерно составляет 1 час, а α₂ достигает величины почти в 18 часов и соответствующая дуга охватывает три четверти длины линии небесного экватора.
Формула расчета углового расстояния выводится с помощью тригонометрических преобразований угловых параметров треугольников соединяющих точки, соответствующие положению объектов на небесной сфере, центр этой сферы и точки отсчета склонений объектов:

при использовании численных методов, важно помнить что arccos(x)=0 при x=1, во избежание деления на 0.

Примечательные угловые расстояния

Самые интересные возможности программы расчета угловых расстояний между звездами раскрываются при ее применении к таким знаменитым астеризмам [3] как Большой Ковш и Малый Ковш, W Кассиопеи, Большой квадрат и сезонные Треугольники.
Сначала для интереса определим угловой размер Большого Ковша: Внешний край его черпака обозначен звездой Дубхе (α Большой Медведицы, 1,81 m ) и на краю его ручки располагается Бенетнаш (η Большой Медведицы, 1,85m ), выбираем эти звезды из разворачивающего списка расчетного табло и получаем: 25,71092° или 25° 42′39″.
У Малого Ковша соответствующие края определяют Кохаб (β Малой Медведицы, 2,07 m ) и Полярная Звезда (α Малой Медведицы, 1,97 m ), угловое расстояние между ними 16,58° — по этой величине можно калибровать угловое расстояние от большого до указательного пальца.
Размер W Кассиопеи определяется расстоянием между звездами Каф (β Cas; 2,27 m ) и Сегин (ε Cas, 3,37 m ): 13,26°

Развеиваем мифы
(нет в мире совершенства)

Большой квадрат — астеризм из звезд Альферац (α Андромеды, 2.06 m ) — Шеат (β Пегаса, 2.42 m ) — Маркаб (α Пегаса, 2.48 m ) — Альгениб (γ Пегаса, 2.84 m ) на самом деле совсем не квадрат:
Альферац — Шеат: 14,20886°; Шеат — Маркаб: 12,87202°;
Альгениб — Маркаб: 16,51628°; Альферац — Альгениб: 13,95490°.

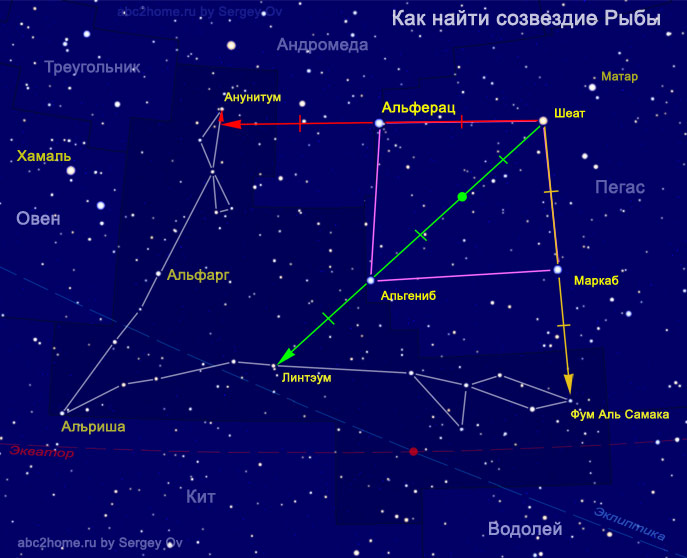
На данный момент на сайте нет детального описания древнейшего астеризма Большой Квадрат, но иллюстрация с его довольно крупным изображением есть:

Рис. 2. Как найти созвездие Рыбы с помощью астеризма Большой Квадрат

Как видно из рисунка Большой Квадрат, на самом деле, по конфигурации наиболее близок к трапеции. Для представленных далее астеризмов сезонных Треугольников на сайте имеется хоть какое-то писание и иллюстрации, поэтому для желающих ознакомиться с этими звездными объектами расставлены ссылки на страницы с их изображениями.

Зимний треугольник: астеризм из звезд Бетельгейзе (α Ориона; 0,45 m ), Сириус (α Большого Пса, -1,45 m ) и Процион (α Малого Пса, 0,40 m ):
Бетельгейзе — Сириус: 27,11047°

26° — без одного градуса равносторонний треугольник!

Весенний треугольник: Арктур (α Волопаса, -0,04 m ), Спика (α Девы, 0,98 m ), Денебола (β Льва, 2,14 m )
Арктур — Спика: 32,78940°;
Спика — Денебола: 35,06157°;
Денебола — Арктур: 35,30957° — без нескольких угловых минут равнобедренный треугольник, хотя его все считают правильным. Наиболее древним вариантом Весеннего Треугольника считается треугольник, третьей вершиной которого вместо не очень яркой Денеболы является Регул (α Льва, 1,4 m ).

Летне-осенний треугольник: Вега (α Лиры, 0,03 m ), Денеб (α Лебедя, 1,25 m ) и Альтаир (α Орла, 0,77 m ).
Вега — Денеб: 23,84870°;
Денеб — Альтаир: 38,01195°;
Альтаир — Вега: 34,19057° — просто треугольник из ярких звезд, с помощью которого можно легко найти созвездия Стрелец и Козерог.

P.S. На этой странице используется Бета версия программы расчета между двумя небесными объектами, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Эфемеридами называются рассчитанные наперед угловые координаты небесных тел. если подходить к современному понятию строго, то ЭФЕМЕР́ИДЫ (астрономический термин), координаты небесных светил и др. переменные астрономические величины, вычисленные для ряда последовательных моментов времени и сведенные в таблицы.

2. Прямое восхождение и склонение — название координат во второй экваториальной системе отсчета.
Для определения положения светила s проводят через небесный экватор и Р (полюс мира) большой круг, называемый часовым кругом, или кругом склонений. Дуга этого круга от экватора до светила есть первая координата — склонение светила d (δ). Склонение отсчитывается от экватора в обе стороны от 0° до 90°, причём для светил Южном полушария d (δ) принимается отрицательным.
. Восхождение светила a (α) — дуга α₁ небесного экватора (Рис.1), отсчитываемая от точки весеннего равноденствия в направлении, обратном вращению небесной сферы, до круга склонений данного светила. Она измеряет сферический угол между кругами склонений, проходящими через точку равноденствия и данное светило. Обычно ее выражается в часах, минутах и секундах времени и может иметь любое значение от 0ч до 24ч

3. Астеризм — группа звезд, образующая характерный рисунок и имеющая самостоятельное название. Астеризм может быть как частью созвездия, например, Трон, так и объединять несколько созвездий, например, Зимний Треугольник.

Большой российский энциклопедический словарь. 2012

Источник

Презентация по астрономии на тему «Способы определения углового расстояния между астрономическими объектами»

В презентации кратко описаны способы определения углового расстояния между астрономическими объектами — как теоретически обоснованные и общепринятые, так и «народные».

Скачать:

Вложение	Размер
zaharov_11a_s_pravkami_otmetka_5_.pptx	426.83 КБ

Предварительный просмотр:

Подписи к слайдам:

Способы определения углового расстояния между астрономическими объектами. Выполнил воспитанник 11 А : Захаров Алексей Евгеньевич Преподаватель: Богданенко Елена Николаевна ГБОУ РО «НШИ с ПЛП» Таганрог, 2020

Угловое расстояние Угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов.

Определение угловых размеров на небе с помощью руки Для того чтобы научиться искать созвездия на ночном небе, для начала, достаточно знать древнейший астеризм «Большой Ковш» — его семь звезд, самых ярких в созвездии Большая Медведица, являются направляющими (путеводными) для поиска звезд в других созвездиях. На примере астеризма Ковш созвездия Большая Медведица показаны угловые расстояния между звёздами, а также схематически вытянутая рука и расстояние между пальцами. Например, «ширина» мизинца равна 1°, кулак — 10°, «коза» с большим пальцем — 20°.

Вариант с 3 — 4 — 6° выглядит очень любопытно. Во-первых, позволяет определить расстояние между объектами, которые лежат не на одной линии, а во-вторых, косточки указательного пальца так же могут выступать в качестве линейки. Ещё один вариант определения углового размера.

Как найти созвездие Малая Медведица Поиск созвездия Малой Медведицы обычно все начинают с поиска Полярной Звезды , чтобы найти Полярную Звезду нужно мысленно провести линию между звездами края Ковша от Мерак к Дубхе и продолжить до первой яркой звезды — это и будет Полярная Звезда, указывающая направление на Север! Полярная Звезда является важнейшей навигационной звездой, а Мерак и Дубхе , помогающие ее найти, еще называют Указателями.

Как найти созвездие Кассиопея Всесезонный способ определения местоположения Кассиопеи, заключается в «нацеливании» луча, через уже известные звезды. Самый лучший «выстрел» получится если продолжить линию от Алиот (ε UMa ) за Полярную Звезду (α UMa ) при этом получится точное попадание в Гамма Кассиопеи Нави (γ Cas ), к тому же приглядевшись, Вы обнаружите, что Большой Ковш и астеризм Трон Кассиопеи расположены центрально-симметрично относительно Полярной Звезды.

Расчет углового расстояния между двумя астрономическими объектами Во второй экваториальной системе координат положение объектов определяется двумя угловыми параметрами, называемыми прямое восхождение α и склонение δ. β — это угловое расстояние между двумя небесными объектами, α 1 и δ 1 , прямое восхождение и склонение, характеризующие положение Объекта 1 на небесной сфере, соответственно, положение Объекта 2 характеризуется α 2 и δ 2 . Склонение определяется величиной угла от линии небесного экватора до объекта в плоскости перпендикулярной экватору. Прямое восхождение определяется величиной угла между точкой весеннего равноденствия и точкой отсчета склонения. Важно запомнить, что прямое восхождение отсчитывается от точки весеннего равноденствия в направлении противоположном движению часовой стрелки (в точке весеннего равноденствия Солнце вступает в знак Овна) и его величина выражается не градусах, а в часах .

Расчет углового расстояния между двумя астрономическими объектами, положение которых определено во второй экваториальной системе координат На рисунке величина α 1 примерно составляет 1 час, а α 2 достигает величины почти в 18 часов и соответствующая дуга охватывает три четверти длины линии небесного экватора. Формула расчета углового расстояния выводится с помощью тригонометрических преобразований угловых параметров треугольников соединяющих точки, соответствующие положению объектов на небесной сфере, центр этой сферы и точки отсчета склонений объектов : β = arccos ( sin (δ 1 )* sin (δ 2 )+ cos (δ 1 )* cos (δ 2 )* cos (α 1 — α 2 )) ,

Источник