Удобный способ вычисления 5 класс формула

Основные правила и свойства вычитания для 5 класса

Учащиеся средних образовательных школ изучают в 5 классе свойства вычитания и сложения. Они применяются для решения примеров, ускорения вычислений в устной форме и т. д. В высших учебных заведениях правила используются для упрощения выражений, нахождения корней дифференциальных уравнений и пределов, а также для выполнения других операций.

Общая информация

Вычитание — операция уменьшения числа на определенное значение. Для примера следует записать следующее выражение: p — t = v. Первая величина называется уменьшаемым, вторая — вычитаемым, а результат вычитания — разность. Очень часто в литературе с физико-математическим уклоном можно встретить связку «разность двух чисел», которая является синонимом вычитания.

Сложение — математическая операция, применяемая для увеличения числа на некоторое значение. Коэффициенты имеют такие названия (p + t = v):

1. p — первое слагаемое.
2. t — второе слагаемое.
3. v — сумма.

Формулировка сочетательного закона сложения следующая: чтобы прибавить к сумме двух чисел, сгруппированных в скобках, третью величину, необходимо осуществить операцию сложения первого и третьего, а затем к результату прибавить второе слагаемое. В буквенном виде он записывается в таком виде: (t + v) + s = (t + s) + v. Справедлива будет и такая запись: (t + v) + s = (v + s) + t. Переместительный и сочетательный законы позволяют группировать слагаемые в любой последовательности.

Методы вычитания

Для выполнения операции разности чисел нужно придерживаться определенных свойств вычитания. В 5 классе изучаются все необходимые формулы и утверждения, к которым можно отнести следующие:

1. При вычитании 0 из числа получается искомое число: t — 0 = t.
2. Если из нулевого значения вычесть число, результат будет эквивалентен величине, взятой со знаком «- «: т. е. 0 — t = -t.
3. Разность двух чисел, эквивалентных между собой, соответствует нулевой величине: t — t = 0.
4. Для вычитания суммы двух слагаемых из числа нужно из последнего вычесть первое слагаемое, а затем второе: t — (s + v) = t — s — v.
5. Чтобы вычислить разность суммы двух слагаемых и вычитаемого, нужно отнять из первого слагаемого вычитаемое, а затем к результату прибавить II слагаемое: (t + s) — v = t — v + s.
6. Если одним из слагаемых является разность двух чисел (составное), необходимо к первому значению прибавить уменьшаемое, а затем из результата вычесть вычитаемое: t + (s — v) = t + s — v.

В шестом законе вычитания для 5 класса требуется просто раскрыть скобки без изменения знаков величин. Специалисты рекомендуют записать все правила в специальные таблицы-тренажеры, которые должны всегда быть под рукой.

Таким образом, для выполнения арифметических операций сложения и вычитания нужно знать все основные свойства и формулы, позволяющие оптимизировать вычисления.

Источник

Урок 26 Бесплатно Формулы

Сегодня на уроке мы выясним, что называют формулой и где её применяют.

Разберем правила решения и оформления задач, решаемых с помощью формул.

Рассмотрим примеры таких задач и научимся работать с формулами: выражать неизвестные величины через известные.

Формулы

Математический язык- это формальный, искусственно созданный язык, который состоит из математических знаков, символов, терминов, выражений.

В отличие от естественных языков, этот язык более точный, логичный и краткий.

При переходе с разговорного языка на математический многие утверждения, правила, законы становятся яснее и прозрачнее.

Математика, физика, химия и многие другие науки используют язык математики, который в условной форме позволяет представить информацию наглядно и лаконично, не искажая ее при этом.

Естественными языками легче всего выражать качественные характеристики посредством красноречивых предложений.

Математический язык- это в большей степени количественный язык.

Одним из базовых элементов математического языка являются формулы.

У меня есть дополнительная информация к этой части урока!

Давайте разберёмся, что означает слово «Формула».

Значение слова «формула» (от латинского formula- образ, вид) в толковом словаре Ушакова означает — выраженный условными знаками ряд математических величин в их функциональных зависимостях.

В толковом словаре русского языка Ожегова есть еще одно интересное толкование этого слова: формула- комбинация математических знаков, выражающая какое-нибудь утверждение

Обобщая все выше написанное, можно сказать, что формула- это правило (высказывание), записанное на математическом языке с помощью осмысленной комбинации знаков и символов.

Формулы представляют собой некоторые суждения, которые понятны любому человеку, любой национальности, и неважно каким разговорным языком человек владеет.

В формулу входят переменные. Она устанавливает взаимосвязь между величинами, входящими в нее.

Любые правила, записанные с помощью букв, будут являться примерами формул.

Вам уже известны некоторые математические формулы.

Приведем несколько примеров.

Правило нахождения периметра треугольника: Р_АВС = a + b + c— формула.

Правило нахождения периметра прямоугольника: Р = 2(a + b)— формула.

Пройти тест и получить оценку можно после входа или регистрации

Решение задач с помощью формул

Нам часто приходится сталкиваться с решением различных задач.

Решить задачу — это значит через логически верную последовательность математических положений, действий и операций с объектами, величинами, числами выполнить требования задачи, т.е. найти верный ответ.

Существуют различные способы и методы решения задач.

Рассмотрим один из них: решение задач с помощью формул.

Процесс решения задач данным способом можно разделить на несколько основных этапов.

Данная последовательность действий не даст ответа на конкретную задачу, но сделает решение ее более понятным и быстрым и позволит решить даже самые непростые задачи.

Рассмотрим общие правила решения задач с помощью формул.

1. Внимательно прочитать, осмыслить и изучить условие задачи.

Следует установить то, что необходимо найти и что известно.

В задачах в основном содержится только существенная информация, т.е. те данные, которые могут быть использованы при их решении.

2. Для лучшего понимания задачи можно ее условия изобразить графически при помощи рисунка, схемы, чертежа и т.д.

С помощью иллюстрации легче понимать и воспринимать информацию.

3. Определить характерные черты задачи.

Следует понять, какого рода задача, чтобы выбрать верный путь ее решения.

Необходимо определить, какими величинами можно описать происходящие процессы, явления, действия, а также важно выяснить, из какой темы будут взяты формулы (если задача сложная, то могут понадобиться несколько формул).

4. Составить план решения задачи.

5. Выразить неизвестную величину через известные величины, т.е. вывести расчетную формулу.

6. Подставить известные числовые значения и произвести вычисления.

7. Оценить размерность (соответствие единиц измерения) величины, полученной в ответе, проверить найденный ответ на наличие вычислительных ошибок.

8. Записать ответ.

Чтобы верно и быстро решить задачу, важно не только действовать четко по определенному алгоритму, но и грамотно записывать и оформлять решение этой задачи.

Задачи, решаемые с помощью формул, удобно делить на два блока: «Дано» и «Решение».

В «Дано» обычно с помощью букв или символов записывают заданные величины и величины, которые требуется определить; т.е. кратко обозначают условие задачи.

Можно использовать любые буквы для обозначения заданных и искомых величин, но тогда необходимо делать краткое описание того, какую величину обозначает та или иная буква, выбранная вами.

Однако чаще всего буквенные обозначения величин, если они не указаны в условиях задачи, выбираются в соответствии с принятыми в науке символами.

Многие величины уже имеют специальные обозначения.

Например, периметр принято обозначать буквой Р, длину и ширину буквами a и b, пройденный путь — S, скорость буквой V, время — t и т.д.

Каждая величина имеет единицу измерения.

Сразу в «Дано» переводят единицы измерения в единую систему, так как одна и та же величина должна быть выражена единой единицей измерения.

Иногда в задачах одноименные величины могут быть выражены разными числовыми мерами.

Например, расстояние может быть выражено в одной и той же задаче километрами, метрами и сантиметрами, или время может быть представлено в одном условии задачи в часах, в другом условии этой же задачи в минутах.

В таком случае необходимо выполнить перевод из разных единиц измерения в одну общую, которая будет фигурировать при числовых подсчетах.

У меня есть дополнительная информация к этой части урока!

Чаще всего выбор единиц измерения диктуется установленными международными нормами.

Наиболее широко используемой системой единиц в мире является единая интернациональная система. Называется она сокращенно «Система СИ».

Система СИ принята как основная система единиц в большинстве стран мира.

Страны, которые используют традиционные единицы, ввели коэффициенты и поправки, чтобы связать свои единицы измерения с системой СИ.

СИ создана на основе метрической системы, которая была создана французскими учеными. (с метрической системой мы немного познакомились, рассматривая тему «Отрезок. Длина отрезка.»).

Система СИ определяет семь основных единиц и производные единицы, а также набор приставок.

Системой СИ установлены стандартные сокращенные обозначения единиц.

Источник

Удобный способ вычисления 5 класс формула

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число меньше любого натурального числа.

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

Свойства сложения

Переместительный закон:

Сочетательный закон:

Формула пути

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

• Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

• Чтобы найти неизвестное уменьшаемое, надо к разности при­бавить вычитаемое.

• Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

• Чтобы найти неизвестный множитель, надо произведение раз­делить на известный множитель.

• Чтобы найти неизвестное делимое, надо делитель умножить на частное.

• Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

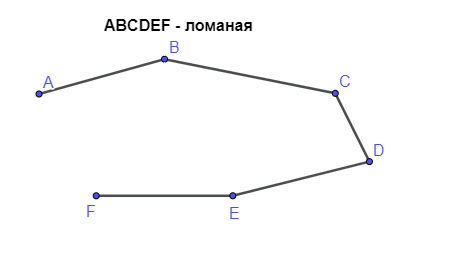
Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

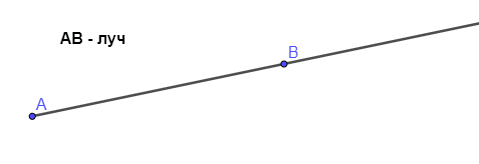
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

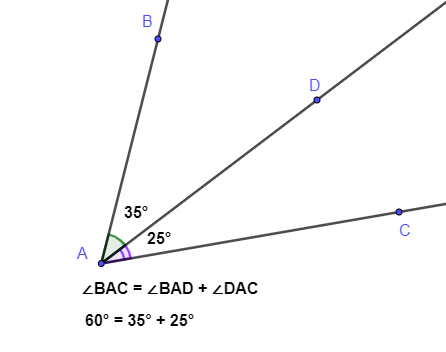
Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники. Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

• Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

• Если один из двух множителей равен 1, то произведение равно второму множителю.

• Если один из множителей равен нулю, то произведение равно нулю.

• Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

• Переместительный закон умножения:

• Сочетательный закон умножения:

• Распределительное свойство умножения относительно сложения:

• Распределительное свойство умножения относительно вычитания:

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

,

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

,

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

• ,

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

• ,

где — площадь основания параллелепипеда, — его высота.

Объем куба

,

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

• Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

• Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

• Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

• числитель разделить на знаменатель;
• полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

• целую часть числа умножить на знаменатель дробной части;
• к полученному произведению прибавить числитель дробной части;
• эту сумму записать как числитель неправильной дроби;
• в его знаменателе записать знаменатель дробной части смешанного числа.

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

• с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
• после чего сравнить полученные дроби поразрядно.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

• все следующие за этим разрядом цифры отбросить.
• если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4 , то последнюю из цифр, которые оставляют, не меняют ;
• если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9 , то последнюю из цифр, которые оставляют, увеличивают на единицу.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
• сложить полученные числа так, как складывают натуральные числа;
• поставить в полученной сумме запятую под запятыми.

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

• уравнять количество цифр после запятых;
• записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
• выполнить вычитание так, как вычитают натуральные числа;
• поставить в полученной разности запятую под запятыми.

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

• перемножить их как натуральные числа, не обращая внимания на запятые;
• в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

• перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
• выполнить деление на натуральное число.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15 + 25 + 20 ⏞ с у м м а ч и с е л 3 ⏟ к о л и ч е с т в о ч и с е л = 60 3 = 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

V с р е д н я я = S о б щ t о б щ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Процент

Процентом называют сотую часть величины или числа 1%=

Основные правила математики с примерами. 5 класс: 22 комментария

Спасибо большое! Я решил вспомнить материал по математике и вы мне с этим помогли

Уважаемая Наталья Владимировна! По структуре и подаче материала — это лучшее, что мне удалось найти на просторах интернета. Спасибо вам за труд!

Пожалуйста! Я очень рада, что Вы высоко оценили мой труд.

Спасибо огромное ! У меня завтра впр , и я надеюсь я получу 5 😇💖

Источник