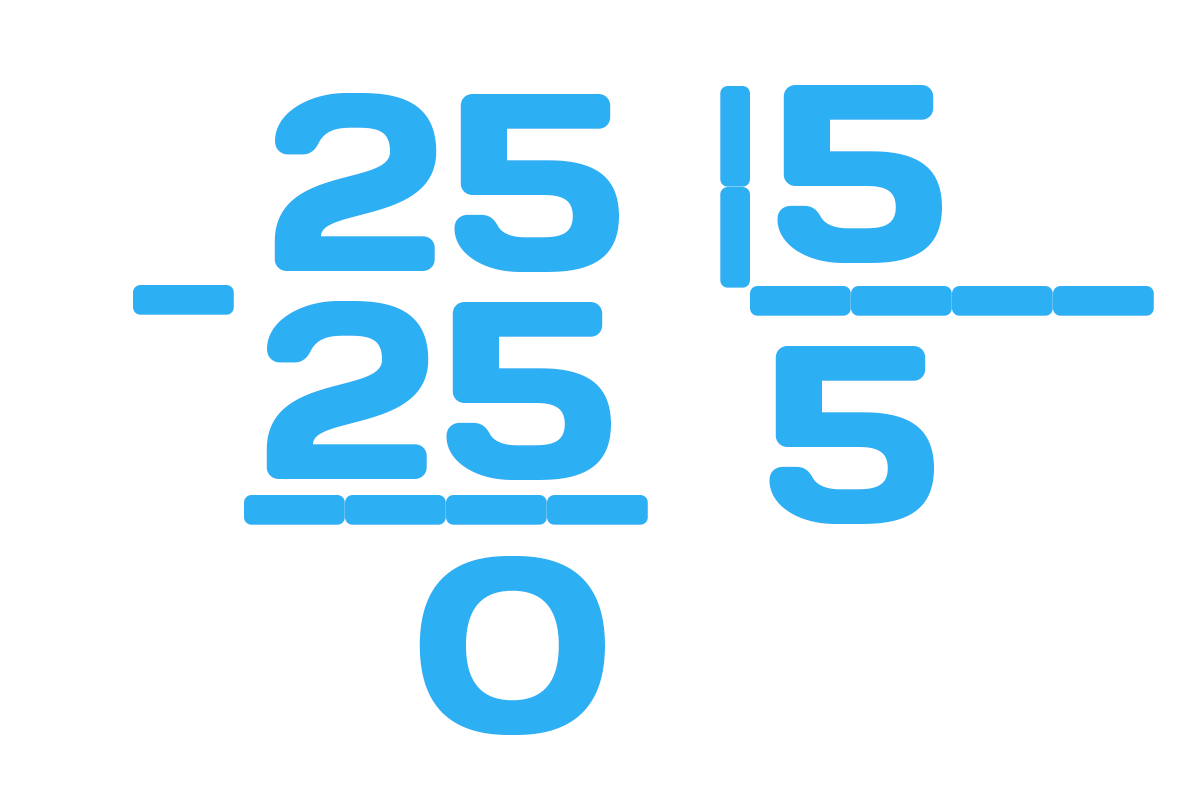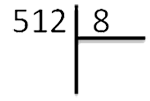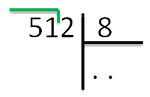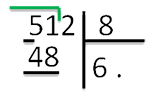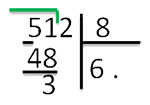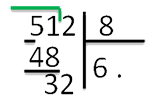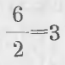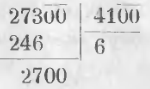Удобный способ деления чисел

Деление

Деление – одна из четырех основных математических операций (сложение, вычитание, умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение. 3*3=9. Верно? Абсолютно.

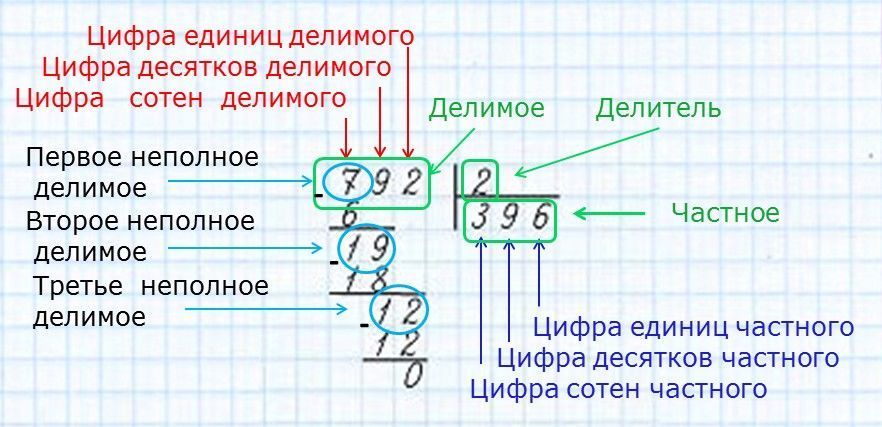
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение. В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2. На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4. Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

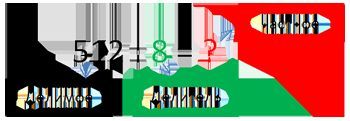
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

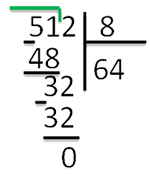
Рассмотрим пример, 512:8.

1 шаг. Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг. Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг. Ставим точку под делителем.

5 шаг. После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!

Источник

Математика

Определить, сколько раз нужно взять слагаемым меньшее число 2, чтобы получить большее число 6, значит определить, сколько раз число 2 содержится в 6, или сколько раз число 6 содержит 2.

Число 2 содержится в 6 три раза, ибо, чтобы получить 6, нужно взять сумму трех равных слагаемых:

Найти, сколько раз число 2 содержится в 6, значит разделить 6 на 2.

Определение. Деление есть такое действие, в котором по двум данным числам определяют, сколько раз одно число содержится в другом.

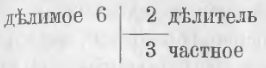
Данные числа в делении называются делимым и делителем, искомое называется частным.

Делимое есть то число, которое содержит другое.

Делитель есть то число, которое содержится в другом.

Частное показывает, сколько раз делитель содержится в делимом.

В данном примере делимое есть 6, делитель 2, частное 3.

Разделить 6 на 2 значит также разбить 6 на 2 равных слагаемых и отыскать их величину. Число 6 представится при помощи двух равных слагаемых в виде:

Каждое из равных слагаемых называется частью делимого.

Посредством деления целых чисел также узнается, как велико каждое слагаемое, если делимое разобьется на столько равных слагаемых, сколько в делителе единиц.

В этом случае делимое есть то число, которое делится или разбивается на равные части. Делитель показывает, на сколько равных частей делится делимое. Частное показывает, сколько приходится на каждую часть.

Способы деления

Имея два числа 12 и 4, мы можем разделить 12 на 4 различными способами.

С помощью сложения мы можем определить, сколько раз нужно взять 4 слагаемым для того, чтобы получить в сумме 12. Так, взяв 4 слагаемым 3 раза, находим в сумме:

следовательно, 4 содержится в 12 три раза.

С помощью вычитания определяем, сколько раз можно из большего числа 12 вычесть меньшее 4. При этом мы вычитаем делитель до тех пор, пока это возможно. Так, вычитая последовательно из 12 по 4, имеем:

12 — 4 = 8
8 — 4 = 4
4 — 4 = 0

Отсюда находим, что можно вычесть 4 из 12 ровно три раза.

Деление есть сокращенное вычитание равных вычитаемых.

Наконец, посредством умножения, мы можем определить, на какое число нужно помножить 4, чтобы получить 12. Умножая последовательно 4 на 1, 2, 3, находим, что для того, чтобы получить 12, нужно 4 помножить на 3.

Различные случаи при делении

При делении целых чисел бывают два случая:

Разделяя 12 на 4, мы находим в частном 3. Делитель 4 содержится ровно 3 раза в делимом 12. Вычитая последовательно из 12 по 4, мы могли вычесть число 4 ровно три раза и не получили никакого остатка. В этом случае говорят, что деление совершилось нацело или без остатка. Умножив частное 3 на делитель 4, получаем делимое 12.

Разделяя 26 на 8, мы при последовательном вычитании получаем:

26 — 8 = 18
18 — 8 = 10
10 — 8 = 2

Далее нельзя продолжать вычитания, потому что из 2 нельзя вычесть делитель 8. Число 2 называют остатком.

Остаток всегда меньше делителя. В этом случае говорят, что деление не совершается нацело или деление совершается с остатком.

Разделяя 26 на 8, мы могли вычесть делитель 8 три раза, и у нас получился остаток 2. Число 3 мы будем называть целым частным. Целое частное есть не полное частное, ибо оно не выражает вполне, сколько раз меньшее число содержится в большем. Число 8 не содержится в 26 ровно 3 раза. В этом случае говорят: число 8 содержится в 26 три раза и еще получается остаток. Умножив делитель 8 на целое частное 3, мы не получим делимого 26, а число 24 — меньшее делимого. Чтобы получить делимое, нужно к этому произведению прибавить еще остаток 2.

Целое частное иногда называют просто частным.

Итак, при делении мы имеем два случая:

Деление нацело или без остатка. Когда делитель содержится в делимом ровное число раз, тогда деление совершается нацело или без остатка. Частное выражает, сколько раз делитель содержится в делимом. Делимое равно делителю, умноженному на частное. В этом случае деление есть действие в котором по данному произведению и одному из производителей находится другой производитель.

Если дается произведение и множимое, отыскивают множитель, то есть число равных слагаемых; если дается произведение и множитель, отыскивают множимое, то есть величину равных слагаемых.

Деление с остатком. Когда делитель не содержится в делимом ровное число раз, тогда деление не совершается нацело, или деление совершается с остатком. Остаток всегда меньше делителя и делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении целых чисел делимое всегда уменьшается во столько раз, сколько в делителе единиц, поэтому деление есть действие, обратное умножению.

Знак деления

Действие деления изображается знаком двоеточия ÷, который ставится между делимым и делителем.

Деление числа 6 на 2 изображают письменно:

6 ÷ 2 = 3 частное.

Действие деления обозначается также начертанием |–, где вертикальная черта отделяет делимое, а горизонтальная делитель от частного.

В данном примере имеем:

В нашем примере деление изображается письменно:

Знак деления прешел к нам от древних математиков.

Основные приемы при делении

Делить значит последовательно вычитать делитель из делимого, пока это возможно. Этот способ деления можно считать общим. Прием этот, однако, приводит к длинным вычислениям, если делимое очень велико, поэтому существуют различные сокращенные приемы деления.

Чтобы определить частное в том случае, когда оно выражается одной цифрой, прибегают к таблице умножения.

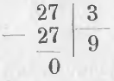
Чтобы разделить 27 на 3 мы пишем

Для частного выбираем такое число, чтобы, умножив делитель на частное, получить делимое. Чтобы найти цифру частного, мы пробуем умножать делитель на разные числа или, как обыкновенно говорят, задаемся разными числами, и сравниваем произвдение делителя на частное с делимым.

Разделяя 27 на 3 и перебирая в уме все произведения 3 на разные числа, содержащиеся в таблице умножения, находим, что произведение 3 × 9 составляет 27 и потому пишем в частном 9. Вычитая произведение делителя на частное из делимого, получаем в остатке нуль.

Само вычисление выражают письменно:

Деление совершилось нацело.

Иногда делитель не содержится в делимом ровное число раз; так, разделяя 27 на 4, мы не находим в таблице целого числа, которое, будучи помножено на 4, дало бы 27; тогда деление не совершается нацело.

Отыскивая целое частно, мы имеем при этом три случая:

Или мы задаемся очень малым числом; так, для данного примера, задавшись в частном 5 и умножив 4 на 5, имеем 20. Подписав произведение 20 под делимым и вычитая из 27, имеем:

в остатке число 7 больше делителя 4. Это показывает, что частное 5 мало и его нужно увеличить.

Или, взяв для частного 7 и умножив его на делителя 4, получаем произведение 28 больше делимого, что показывает, что мы задались в частно очень большим числом. В таком случае нужно уменьшить цифру частного 7.

Взяв для частного 6, мы ход вычисления выражаем письменно:

словесно: 4 в 27 содержится 6 раз, 4 * 6 = 24, подписываем 24 под делимым, вычитаем и получаем остаток 3. Остаток 3 меньше делителя, следовательно, цифра частного верна. Отсюда выводим следующее:

Правило определения частного:

Если при делении остаток более или равен делителю, цифра частного мала и ее нужно увеличить.

Если произведение делителя на частное больше делимого, цифра частно велика и ее нужно уменьшить.

Если остаток меньше делителя, цифра частного верна.

Это правило показывает, что при делении нужно для частного выбирать такое число, чтобы остаток был меньше делителя. Задаваться так, значит задаваться наибольшим целым числом.

В данном примере 27 не делится нацело на 4, а получается остаток 3; число 6 есть целое частное и

27 = 4 × 6 + 3 = 24 + 3

Делимое 27 равно произведению делителя 4 на целое частное 6, сложенному с остатком 3.

Деление многозначного числа на однозначное

Частное от деления многозначного числа на однозначное иногда выражается числом, состоящим также из нескольких цифр. В этом случае деление распадается на несколько отдельных действий.

Разделим 702 на 3. Частное содержит три цифры. Оно больше 100 и меньше 1000, ибо делимое больше 300 (3 × 100) и меньше 3000 (3 × 1000). Включая три цифры, частное содержит сотни, десятки и единицы. В данном случае разбиваем деление на три отдельных действия, то есть отыскиваем последовательно сотни, потом десятки и, наконец, единицы частного. Самое действие начинаем с сотен.

Отыскиваем сотни частного. Цифра сотен частного может происходить от деления сотен делимого на делитель 3. Десятки и единицы делимого не имеют никакого влияния на сотни частного, поэтому на них пока не обращаем внимания. Наибольшее число сотен в частном есть 2, ибо 3 содержится в 7 сотнях 2 сотни раз; пишем в частном 200. Умножая 200 на 3 и вычитая произведение 600 из делимого, получаем первый остаток 132.

Отыскиваем десятки частного. В остатке 132 находится 12 десятков. Единицы делимого не имеют влияния на десятки частного. Разделив 13 на 3, находим, что в частном могут быть только 4 десятка, — пишем 40 в частном. Умножая 40 на 3 и вычитая произведение 120, получаем в остатке 12.

Отыскиваем единицы частного. Разделив 12 на 3, находим для единиц частного 4. Умножая 4 на 3 и вычитая произведение 12, получаем в остатке 0.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, деление изобразится письменно:

Отделяем 7 — одну цифру делимого; 3 в 7 содержится 2 раза, — пишем в частном 2; умножая на нее делителя 3 и вычитая произведение 6 из 7, получаем первый остаток 1.

Сносим 3 — следующую цифру делимого; 3 в 13 содержится 4 раза, 3-жды 4 составляет 12; вычитая 12 из 13, получаем в остатке 1.

Сносим 2 следующую цифру делимого; 3 в 12 содержится 4 раза, пишем в частном 4; 3-жды 4 составляет 12. Вычитая 12, получаем в остатке нуль и в частном 244.

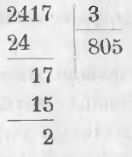
Пример. Разделить 2417 на 3. Ход вычисления выразится письменно:

Отделив одну цифру 2, мы видим, что 3 в 2 не содержится целое число раз, поэтому нужно отделить две цифры; 3 в 24 содержится 8 раз, — пишем 8 в частном. Умножив 8 на делителя 3 и вычитая произведение 24, получаем в остатке нуль.

Сносим следующую цифру 1; 3 в 1 не содержится, — пишем в частном нуль.

Сносим следующую цифру 7; 3 в 17 содержится 5 раз, — пишем в частном 5; 3-жды 5 составляет 15; вычитая 15 из 17, получим в остатке 2 и целое частное 805.

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

Определяем сотни частного:

Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

Определяем десятки частного:

Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

Определяем единицы частного:

47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.

Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.

Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

К остатку сносят следующую цифру делимого и снова задаются.

Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

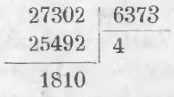
Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя. Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр. Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

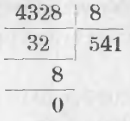
Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Деление на 10, 100, 1000 и т. д.

Разделяя число на 10, мы десятки делимого обращаем в единицы, сотни в десятки, тысячи в сотни, вообще понижаем на единицу все порядки делимого. Этого мы достигаем, отделяя запятою цифру единиц. Число до запятой будет выражать частное, а после запятой — остаток.

Разделяя на 100, мы понижаем все порядки делимого на две единицы, для чего отделяем запятою от правой руки к левой две цифры и т. д. Отсюда правило:

Чтобы разделить какое-нибудь число на единицу с нулями, нужно от правой руки к левой отделить столько цифр, сколько нулей в делителе; тогда число до запятой выражает целое частное, а после запятой — остаток.

Пример. Разделяя 30207 на 100. Отделяя справа 2 цифры, находим 302,07. Целое частное будет 302, а остаток 7.

Деление на число, оканчивающееся нулями

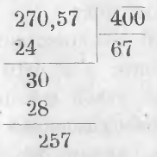
Разделяя число 27057 на 400 и поступая при этом по общему правилу

мы замечаем, что две последние цифры делимого не оказывают никакого влияния на частное. Они являются в остатке без всякой перемены. Откуда правило:

Если делитель оканчивается нулями, отделяют в делимом запятою от правой руки к левой столько цифр, сколько зачеркнуто нулей в делителе, и делят часть делимого до запятой на значащие цифры делителя. Отделенные цифры делимого приписывают к остатку.

В данном примере деление представится в виде

f

Если делимое и делитель оканчиваются нулями, их зачеркивают поровну в делимом, делителе и производят деление; зачеркнутые нули делимого приписывают к остатку.

Чтобы разделить 27300 на 4100, делим 273 на 41:

Частное будет 6, а остаток 2700.

Число цифр частного. При делении отделяют в делимом от левой руки к правой столько цифр, сколько их находится во делителе, или одною больше. Каждой оставшейся цифре делимого соответствует особая цифра частного, следовательно, число цифр частного будет равно или разности числа цифр делимого и делителя или на единицу больше этой разности .

Зависимость между данными и искомыми деления

При делении целых чисел мы имеем два случая: а) деление нацело, или без остатка, и б) деление с остатком.

Каждому из этих случаев соответствует особая зависимость между данными и искомыми деления.

Деление нацело или без остатка

При делении нацело

Частное равно делимому, разделенному на делитель.

Разделяя 42 на 7, имеем в частном 6; следовательно,

42 ÷ 7 = 6, или 6 = 42 ÷ 7

Делимое равно делителю, умноженному на частное.

Так как делитель и частное — два множителя, произведение которых равно делимому, то делитель равен делимому, разделенному на частное.

Деление с остатком

При делении с остатком

Делимое равно произведению делителя на целое частное, сложенное с остатком.

При делении 47 на 6, имеем в целом частном 7, в остатке 5.

Делимое 47 = 6 × 7 + 5.

Делимое без остатка делится нацело на делитель и на целое частное.

Разность делимого без остатка равна произведению делителя на целое частное, то есть эта разность при делении на делитель дает целое частное, при делении на целое частное дает делитель.

Источник