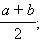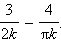Учитель хочет назначить 3 студентов для уборки класс учеников сколькими способами можно это сделать
В настоящее время теория вероятностей завоевала очень серьезное место в науке и прикладной деятельности. Её идеи, методы и результаты не только используются, но и буквально пронизывают все естественные и технические науки.
В нашу жизнь вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов. Общество все глубже начинает изучать себя и стремиться сделать прогнозы о себе самом и о явлениях природы, которые требуют представлений о вероятности. Теория вероятностей не обошла и учебные заведения. В соответствии с федеральным компонентом Государственного стандарта образования и программу по математике за курс основной (средней) школы включены элементы комбинаторики, статистики и теории вероятностей. В последние годы в заданиях государственной итоговой аттестации (с настоящего года – обязательный государственный экзамен) и единого государственного экзамена по математике предлагаются задачи по теории вероятностей и комбинаторике. Поэтому при обучении математике необходима специальная подготовка по обучению учащихся решению таких задач.
В связи с чем цель нашего исследования: выделить основные методы и типы комбинаторных задач и подобрать комплекс таких задач.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач, а раздел математики, в котором рассматриваются подобные задачи, называют комбинаторикой. Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать». Методы комбинаторики находят широкое применение в физике, химии, биологии, экономике, теории вероятностей и других областях науки.
В настоящее время практически во всех учебных пособиях по теории вероятностей выделяют следующие основные методы решения комбинаторных задач: перебор всех возможных вариантов (систематический перебор, перебор с ограничениями), полный граф, дерево вариантов (граф-дерево), таблица вариантов, правила произведения и суммы. Факториал. Перестановки. Размещения. Сочетания. Формулы для подсчёта числа перестановок, размещений и сочетаний. Треугольник Паскаля. Бином Ньютона. Комбинированные задачи.
Проведенный анализ научно-методической литературы 4 позволил выделить следующие типы комбинаторных задач:
· задачи, в которых требуется перечислить все решения;
· задачи, состоящие в требовании выделить из всех возможных решений такое, которое удовлетворяет заданному дополнительному требованию;
· задачи, в которых требуется подсчитать число решений.
Процесс навыков подсчета комбинаторных объектов, по мнению Н.Ш. Кремера [4], можно расчленить на три этапа в зависимости от времени обучения и методов подсчета:
— подсчет методом непосредственного перебора;
— подсчет с использованием комбинаторных принципов;
— подсчет с использованием формул комбинаторики.
Для примера приведем несколько задач из составленного нами комплекса.
Операция перебора раскрывает идею комбинирования, служит основой для формирования комбинаторных понятий, поэтому на первом месте должна стоять задача по формированию навыков систематического перебора.
Пример 1. Из группы теннисистов, в которую входят четыре человека – Сидоров, Петров, Иванов и Шилов, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Составим сначала все пары, в которые входит Сидоров (для краткости будем писать первые буквы фамилий). Получим три пары: СП, СИ, СШ.
Выпишем теперь пары, в которые входит Петров, но не входит Сидоров. Таких пар две: ПИ, ПШ.
Далее составим пары, в которые входит Иванов, но не входит Сидоров и Петров. Такая пара только одна: ИШ.
Других вариантов составления пар нет, так как все пары, в которые входит Шилов, уже составлены.
Итак, мы получили 6 пар: СП, СИ, СШ, ПИ, ПШ, ИШ. Значит, всего существует 6 вариантов выбора тренером пары теннисистов из данной группы.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
Пример 2. Три подруги – Юля, Света и Катя – приобрели два билета на показ мод на 1-е и 2-е места первого ряда. Сколько у подруг есть вариантов занять эти два места в зале?
Если на показ мод пойдут Юля и Света, то они могут занять места двумя способами: 1-е место – Юля, 2-е – Света, или наоборот. Аналогично Юля и Катя, Света и Катя. Таким образом, мы получили 6 вариантов: ЮК, КЮ, ЮС, СЮ, КС, СЮ.
Пример 3. При встрече представителей большой восьмерки они обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
Данную задачу возможно решить методом непосредственного перебора, и уже в самом начале заметим, что довольно сложно перебирать все возможные варианты и не запутаться, не говоря уже о записи решения этой задачи. Но, введя определенные обозначения — кодирование, решение будет очень легко представить.
Каждому представителю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например, число 24 означает что 2-ой представитель пожал руку 4-му. Причем число 35 и 53 означают одно и тоже рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить следующей таблицей:
12, 13, 14, 15, 16, 17, 18,
23, 24, 25, 26, 27, 28,
Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий.
Еще одним способом подсчета комбинаторных наборов является использование правила суммы.
Пример 4. Из класса нужно выделить одного дежурного, девочку или мальчика. Сколько существует способов для выбора дежурного, если в классе 20 мальчиков и 18 девочек?
Выбрать одного мальчика из 20 мы можем 20-ю способами, а одну девочку из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+20) способами.
Для подсчета вариантов мы использовали здесь правило суммы, которое можно сформулировать так: если два действия взаимно исключают друг друга, причем одно из них можно выполнить п способами, а другое – m способами, то какое-либо одно из них можно выполнить n+m способами. В нашем примере действия исключают друг друга, так как мы должны выбрать либо мальчика из одного множества, либо девочку из другого.
Пример 5. Преподаватель хочет назначить троих студентов для уборки аудитории. В группе двадцать семь студентов. Сколькими способами можно это сделать?
Решение. Так как порядок студентов не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27):
Пример 6. В классе из 25 учеников нужно выбрать четырех для научной конференции. Сколькими способами это можно сделать?
Решение. Так как порядок выбранных четырех учеников не имеет значения, то это можно сделать 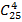
В рассмотренных примерах использовали формулу сочетания.
Пример 7. Имеются 3 путевки в санаторий. Сколько вариантов распределения можно составить для 5 претендентов?
Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.
Пример 8. Расписание одного дня содержит 6 уроков. Определить количество таких расписаний при выборе из 12 дисциплин.
Решение. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.
Примеры 7, 8 решались по формуле размещения.
Пример 9. Сколькими способами семь конфет разных марок можно расставить на прилавке в один ряд?
Решение: эта задача о числе перестановок семи разных конфет. По формуле получаем:
способов осуществить расстановку конфет.
Пример 10. На библиотечной полке стоят 10 книг, причем 8 — книги разных авторов и еще 2 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?
Временно объединим три книги одного автора в один объект, всего получим 9 объектов — 8 книг и 1 объект из двух книг. Для них число перестановок будет 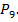
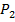
При подсчете конечного результата была использована формула перестановки.
Разработанный нами комплекс задач будет полезен, как учителям математики, так и студентам во время прохождения педагогической практики.
Источник
Методичка к контрольным работам.
Методичка к контрольным работам.
Комбинаторика.
Рассмотрим некоторое множество Х, состоящее из n элементов 
Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор 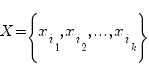
Если выбор элементов множества Y из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по kнаходится по формуле 
Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается 
Пример. Пусть даны цифры: 7; 8; 9; 4; 5; 6. Определить сколько двузначных чисел можно составить из этих цифр.
Решение. Если цифры могут повторяться, то количество двузначных чисел будет 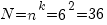

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно 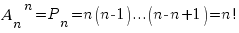
Пример. На библиотечной полке стоят 30 книг, причем 27 — книги разных авторов и еще 3 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?
Решение. Временно объединим три книги одного автора в один объект, всего получим 28 объектов — 27 книг и 1 объект из трех книг. Для них число перестановок будет 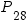

Пусть теперь из множества Х выбирается неупорядоченное подмножество Y (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по kназываются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается 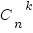

Справедливы равенства:
Пример. Учитель хочет назначить 3 человек для уборки класса из 27 учеников. Сколькими способами можно это сделать?
Решение. Так как порядок учеников не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27):
При решении задач комбинаторики используют следующие правила:
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.
Основные формулы теории вероятностей
Операции над событиями.
Суммой двух событий А и В называется событие АÈВ (А+В), заключающееся в том, что произойдет хотя бы одно из событий А или В (либо событие А, либо событие В либо А и В одновременно).
Произведением (или пересечением) двух событий А и В называется событие АÇВ (АВ), состоящее в одновременном появлении и события А и события В.
Вероятность суммы двух событий вычисляется по формуле (теорема сложения)

События А1,А2. Ак образуют полную группу событий, если в результате испытания непременно произойдет одно из них , т.е. 
События А и В называются несовместными(непересекающимися), если они не могут произойти одновременно АÇВ=Æ. Если события несовместны, то
Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).
Условная вероятность и теорема умножения.
Помимо обычной (безусловной) вероятности можно рассматривать так называемую условную вероятность, вычисляемую при условии, что событие B произошло. Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)
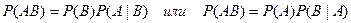
Формула умножения для трех событий:

Независимость событий.

Событие А не зависит от В, если появление события В не меняет значения вероятности события А, т.е. условная вероятность равна безусловной: Р(А/В) = Р(А).Аналогично определяется независимость события B от A.Оказывается, что свойство независимости на самом деле симметрично относительно событий A и B, и потому определение независимости двух событий принимает более простой вид:
два события A и B независимы, если справедливо равенство
Это равенство можно использовать также как удобный критерий независимости при практической проверке независимости двух событий.
Формула полной вероятности.
Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1. n. Предположим, что события Hi несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны. Такие события Hi называются гипотезами. Тогда вероятность события А можно вычислить с помощью формулы полной вероятности:

Для решения задач такое типа удобно использовать так называемое «дерево» вероятностей. Из формулы полной вероятности следует, что для вычисления вероятности события А необходимо осуществить перебор всех путей, ведущих к результирующему событию А; вычислить и расставить на соответствующих путях вероятности Р(Нi) того, что движение будет происходить по данному пути, и вероятности Р(А/ Нi) того, что на данном пути будет достигнуто конечное событие А. Затем вероятности, стоящие на одном пути, перемножаются, а результаты, полученные для различных путей, складываются.
Каждое из условий может в свою очередь делиться на несколько дополнительных условий или гипотез, т.е. на каждом этапе оно допускает неограниченное число ветвлений схемы, поэтому в решении задач удобнее пользоваться не самой формулой полной вероятности, а графической схемой полной вероятности, которую называют «деревом» вероятностей.
Формулы Байеса.
Предположим теперь другую ситуацию: пусть теперь известно, что событие A произошло. Это знание влияет на нашу оценку вероятностей гипотез Нk, т.е. на вероятность того, что событие A произошло именно путем Нk. Эти условные вероятности (т.е. при условии, что событие А произошло), вычисляются с помощью формулы Байеса:

Отметим, что в знаменателе этой формулы записана ничто иное как вероятность Р(А), вычисленная по формуле полной вероятности.
Пример. В магазин привозят товары от трех поставщиков: первый привозит 20%, второй — 30% и третий — 50% всего поступающего товара. Известно, что 10% товара первого поставщика высшего сорта, для второго и третьего поставщика эти значения равны 5% и 20%. Найти вероятность того, что случайно выбранный товар окажется высшего сорта.
Решение. Обозначим через A событие, заключающееся в том, что будет выбран товар высшего сорта. Введем гипотезы 

Применяем формулу полной вероятности:
Пример. В условиях предыдущей задачи найти вероятность того, что товар был привезен первым поставщиком, если он оказался высшего сорта.
Решение. Сохраним обозначения предыдущей задачи (см. выше). Тогда нужно вычислить апостериорную вероятность 
Пример. Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах будет ровно 3 попадания в цель.
Решение. Подставляем в формулу Бернулли данные задачи 
Пример. На склад из производственного цеха поступает в среднем 5% нестандартных деталей. Найти вероятность того, что среди взятых наудачу 10 деталей 2 будут нестандартными.
Решение. Событие А — «появление нестандартной детали», его вероятность 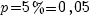


Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тыс. руб. и десять выигрышей по 1тыс. руб. Найти закон распределения случайных величин Х — стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: Напишем возможные значения х: х1=50, х2=1, х3=0. Вероятности этих возможных значений таковы: Р1=1/100=0,01, Р2=10/100=0,1, Р3=89/100=0,89. Напишем искомый закон распределения:
| X | |||
| P | 0.01 | 0.1 | 0.89 |
Пример . Случайная величина Х задана законом распределения
| X | |||
| P | 0.1 | 0.4 | 0.5 |
Найти среднее квадратичное отклонение σ(x)
Решение: Найдем математическое ожидание Х: M(x)=2•0.1+3•0.4+10•0.5=6.4
Найдем математическое ожидание X 2 : M(x 2 )=2 2 •0.1+3 2 •0.4+10 2 •0.5=54
Найдем дисперсию: D(x)=M(x 2 )=M(x 2 )-[M(x)] 2 =54-6.4 2 =13.04
Искомое среднее квадратичное отклонение σ(X)=√D(X)=√13.04≈3.61
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратичных отклонений этих величин:
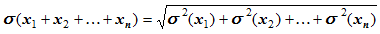
Пример. На полке из 6 книг 3 книги по математике и 3 по физике. Выбирают наудачу три книги. Найти закон распределения числа книг по математике среди выбранных книг. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Введем дискретную случайную величину X = (Количество книг по математике среди 3 отобранных). X может принимать значения 0, 1, 2 и 3. Найдем соответствующие вероятности (по формуле гипергеометрической вероятности).
X=0, если все три книги – не по математике. Вероятность 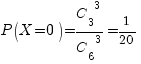
X=1, если одна книга по математике и две – не по математике. Вероятность 
X=2, если две книги по математике и одна нет. Вероятность 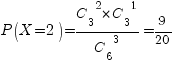
X=3, если все три книги – по математике. Вероятность 
Получаем закон распределения случайной величины X:
xi 0 1 2 3
pi 1/20 9/20 9/20 1/20
Математическое ожидание равно
М(Х 2 ) = 0 2 *1/20 + 1 2 *9/20 + 2 2 *9/20 + 3 2 *1/20 = 2,7
D(X)= М(Х 2 )- М(Х) 2 = 2,7 – 1,5 2 = 0,45
Пример 1
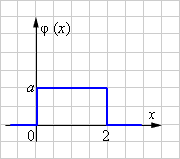
Для некоторого случайного процесса график зависимости плотности вероятности от значения переменной x выглядит следующим образом:
 |
| Рисунок |
Найти величину a.
Если φ (x) – плотность распределения вероятности, то 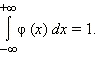 В нашем случае В нашем случае  Следовательно, Следовательно,  Отсюда Отсюда  Обратите внимание, что интеграл от функции равен площади под графиком функции. Следовательно, площадь под графиком функции плотности вероятности φ (x) равна единице. Ответ. Обратите внимание, что интеграл от функции равен площади под графиком функции. Следовательно, площадь под графиком функции плотности вероятности φ (x) равна единице. Ответ.  |
Математическое ожидание величины x для непрерывного распределения, задаваемого плотностью φ (x), определяется формулой
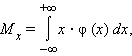 |
а дисперсия – формулой
 |
Среднеквадратичное отклонение по-прежнему задается формулой
 |
Вообще, в том случае, если плотность распределения случайной величины x равна φ (x), математическое ожидание какой-либо функции f (x) этой случайной величины задаётся формулой
 |
1. Постоянное распределение
Распределение, частный случай которого приведён в примере 1, называется постоянным распределением. Его плотность принимает одно и то же значение 
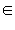

 |
| Рисунок 4.3.7.4. Плотность вероятности постоянного распределения при a = 1, b = 5 |
Пример 2
Вычислить математическое ожидание, дисперсию, среднеквадратичное отклонение случайной величины x, а также среднее значение величины 
Математическое ожидание для непрерывного распределения можно вычислить по формуле 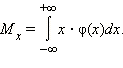 В нашем случае В нашем случае  Этого и следовало ожидать: математическое ожидание величины x должно лежать в точности посередине отрезка [a; b]. Дисперсия Этого и следовало ожидать: математическое ожидание величины x должно лежать в точности посередине отрезка [a; b]. Дисперсия
Среднеквадратичное отклонение
Ответ. Пример 3 Вероятность того, что лампочка перегорит ровно через t дней, подчиняется закону p0 (t) = 0,02 e –0,02t . Найти вероятность того, что 100 дней лампочка будет работать безотказно.
|

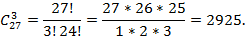
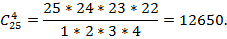
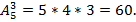
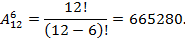
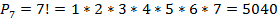

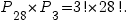


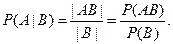


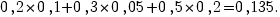



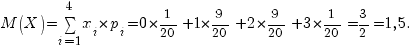
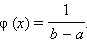

 Наконец, среднее значение величины
Наконец, среднее значение величины