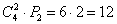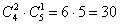У васи дома живут 4 кота сколькими способами можно рассадить 4 который

У васи дома живут 4 кота сколькими способами можно рассадить 4 который

В пенале лежат 4 карандаша: красный, синий, зеленый и желтый.

Сколькими способами можно выбрать из них 4?

Сколькими способами можно раздать по одному карандашу Даше и Ане?

Для того чтобы раздать два карандаша, сначала нужно их выбрать. Согласно теме предыдущего занятия, сделать это можно

способами, запишем их:

Красный и синий; красный и зеленый; красный и желтый; синий и зеленый; синий и желтый; зеленый и желтый.
Но комбинаций сейчас будет в два раза больше. Рассмотрим, например, первую пару карандашей:
красный можно дать Даше, а синий – Ане;
либо, наоборот: синий достанется Даше, а красный – Ане.

И такая перестановка возможна для каждой пары карандашей.

В данном случае можно использовать формулу количества размещений :

Итак, размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их:

В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.

Задача 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.

Задача 2. Сеня, Игорь и Юра сели играть в «очко». Сколькими способами им можно раздать по одной карте из колоды (всего 36 карт)?

Задача 3. В классе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

Задача 4. У Васи дома живут 4 кота.

а) сколькими способами можно рассадить котов по углам комнаты?
б) сколькими способами можно отпустить гулять котов?
в) сколькими способами Вася может взять на руки двух котов (одного на левую, другого – на правую)?

Задача 5. Сколькими способами можно выбрать четырех человек на четыре различные должности, если имеется девять кандидатов на эти должности? А сколькими способами можно выбрать 4-х человек в приемную комиссию? А сколькими способами их можно рассадить в кабинете на 4 стула?

Задача 6. Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами). Сколько различных номерных знаков можно составить для региона?

Источник

Правило сложения и правило умножения комбинаций

1) Знак «плюс» следует понимать и читать как союз ИЛИ. Вспоминаем демонстрационную задачу с яблоком, грушей и бананом:

способами можно выбрать хотя бы один фрукт.

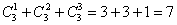
То есть, можно взять 1 фрукт (любой из 3-х) ИЛИ какое-нибудь сочетание 2-х фруктов ИЛИ все три фрукта. Заметьте, что сложение комбинаций предполагает безразличие выбора (без разницы будет ли выбран один, два или 3 фрукта).

Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать 2-х человек одного пола?

Решение: в данном случае не годится подсчёт количества сочетаний 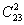, поскольку множество комбинаций из 2-х человек включает в себя и разнополые пары.

Условие «выбрать 2-х человек одного пола» подразумевает, что необходимо выбрать двух юношей или двух девушек, и уже сама словесная формулировка указывает на верный путь решения:

способами можно выбрать 2-х юношей;
способами можно выбрать 2-х девушек.

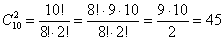
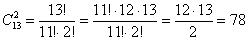
Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: 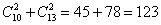способами.

Ответ: 123

Правило умножения комбинаций:

2) Знак «умножить» следует понимать и читать как союз И.

Рассмотрим ту же студенческую группу, которая пошла на танцы. Сколькими способами можно составить пару из юноши и девушки?

способами можно выбрать 1 юношу;
способами можно выбрать 1 девушку.

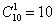
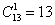
Таким образом, 1-го юношу и 1 девушку можно выбрать: 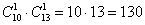способами.

Когда из каждого множества выбирается по 1-му объекту, то справедлив следующий принцип подсчёта комбинаций: «каждый объект из одного множества может составить пару с каждым объектом другого множества».

То есть, Олег может пригласить на танец любую из 13-ти девушек, Евгений – тоже любую из 13-ти девушек, и аналогичный выбор есть у остальных молодых людей. Итого: 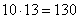возможных пар.

Следует отметить, что в данном примере не имеет значения упорядоченность пары; однако если принять во внимание инициативу, то количество комбинаций нужно удвоить, поскольку каждая из 13-ти девушек тоже может пригласить на танец любого из 10-ти юношей. Всё зависит от условия той или иной задачи!

Похожий принцип справедлив и для более сложных комбинаций, например: сколькими способами можно выбрать 2-х юношей и 2-х девушек для участия в сценке КВН?

Союз И недвусмысленно намекает, что комбинации необходимо перемножить:

возможных групп артистов.

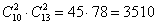
Иными словами, каждая пара юношей (45 уникальных пар) может выступать с любой парой девушек (78 уникальных пар). А если рассмотреть распределение ролей между участниками, то комбинаций будет ещё больше. Правило умножения комбинаций распространяется и на большее количество множителей:

Сколько существует трёхзначных чисел, которые делятся на 5?

Решение: для наглядности обозначим данное число тремя звёздочками: ***

Комбинации будем считать по разрядам – слева направо:

В разряд тысяч можно записать любую из 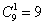цифр (1, 2, 3, 4, 5, 6, 7, 8 или 9). Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.

А вот в разряд десятков («посерединке») можно выбрать любую из 10-ти цифр: .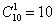

По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас устраивают 2 цифры.

Итого, существует: 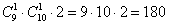трёхзначных чисел, которые делятся на 5.

При этом произведение 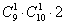расшифровывается так: «9 способами можно выбрать цифру в разряд тысяч и 10 способами выбрать цифру в разряд десятков и 2 способами в разряд единиц»

Или ещё проще: «каждая из 9-ти цифр в разряде тысяч комбинируется с каждой из 10-ти цифр разряда десятков и с каждой из двух цифр в разряде единиц».

Ответ: 180

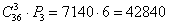
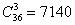
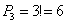
Вернёмся к задаче №5, в которой Боре, Диме и Володе можно сдать по одной карте способами. Умножение здесь имеет тот же смысл: способами можно извлечь 3 карты из колоды И в каждойвыборке переставить их способами.

Задача для самостоятельного решения:

Сколькими способами может быть сдана выигрышная комбинация из 2-х карт при игре в «очко»?

Для тех, кто не знает: выигрывает комбинация 10 + ТУЗ (11 очков) = 21 очко и, давайте будем считать выигрышной комбинацию из 2-х тузов. (К решению этой задачи вернёмся позже)

Кстати, не надо считать пример примитивным. Блэкджек – это чуть ли не единственная игра, для которой существует математически обоснованный алгоритм, позволяющий выигрывать у казино. Желающие могут легко найти массу информации об оптимальной стратегии и тактике.

Пришло время закрепить пройденный материал парой солидных задач:

У Васи дома живут 4 кота.

а) сколькими способами можно рассадить котов по углам комнаты?
б) сколькими способами можно отпустить гулять котов?
в) сколькими способами Вася может взять на руки 2-х котов (одного на левую, другого – на правую)?

Решаем: во-первых, вновь следует обратить внимание на то, что в задаче речь идёт о разных объектах (даже если коты – однояйцовые близнецы). Это очень важное условие!

а) Наказание животных. Данной экзекуции подвергаются сразу все коты
+ важно их расположение, поэтому здесь имеют место перестановки:
способами можно рассадить котов по углам комнаты.

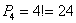
Повторюсь, что при перестановках имеет значение лишь количество различных объектов и их взаимное расположение. В зависимости от настроения Вася может рассадить животных на диване, подоконнике, за столом, под столом и т.д. – перестановок во всех случаях будет 24. Желающие могут для удобства представить, что коты разноцветные (например, белый, чёрный, рыжий и полосатый) и перечислить все возможные комбинации.

б) Сколькими способами можно отпустить гулять котов?

Предполагается, что коты ходят гулять только через дверь, при этом вопрос подразумевает безразличие по поводу количества животных – на прогулку могут выйти 1, 2, 3 или 4 кота.

Считаем все возможные комбинации:

способами можно отпустить гулять одного кота (любого из 4-х);
способами можно отпустить гулять двух котов (варианты перечислите самостоятельно);
способами можно отпустить гулять трёх котов (какой-то один из 4-х сидит дома);
способом можно выпустить всех котов.

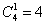
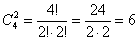
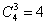
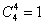
Наверное, вы догадались, что полученные значения следует просуммировать:
способами можно отпустить гулять котов.

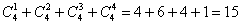
Энтузиастам предлагаю усложнённую версию задачи – когда животные в любой выборке случайным образом могут выйти на улицу, как через дверь, так и через окно. Комбинаций заметно прибавится.

в) Сколькими способами Вася может взять на руки 2-х котов?

Ситуация предполагает не только выбор 2-х животных, но и их размещение по рукам:
способами можно взять на руки 2-х котов.

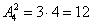
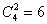
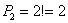
Второй вариант решения: способами можно выбрать двух котов и способами разместить каждую пару на руках:

Ответ: а) 24, б) 15, в) 12

Ну и для очистки совести что-нибудь поконкретнее на умножение комбинаций…. Пусть у Васи дополнительно живёт 5 кошек =) Сколькими способами можно отпустить гулять 2-х котов и одну кошку?

То есть, с каждой парой котов можно выпустить каждую кошку.

Для самостоятельного решения:

В лифт 12-этажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со 2-го) этаже. Сколькими способами:

1) пассажиры могут выйти на одном этаже;
2) два человека могут выйти на одном этаже, а третий – на другом;
3) люди могут выйти на разных этажах;
4) пассажиры могут выйти из лифта?

ДУМЙТЕ, используйте формулы и правила сложения/умножения комбинаций. В случае затруднений пассажирам полезно дать имена и порассуждать, в каких комбинациях Таня, Надя, Люся могут выйти из лифта. Не нужно огорчаться, если что-то не получится, так, например, пункт №2 достаточно коварен.

Источник