У приборов каких систем шкала неравномерная какими способами устраняется неравномерность шкал

Неравномерная шкала СИ

Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют

постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.

Чувствительность — отношение изменения сигнала Δу на выходе СИ к вызвавшему это изменение изменению Δх сигнала на входе

Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины

Таким образом, для неравномерных шкал величина S= var, и степень неравномерности шкалы оценивают через коэффициент

Для равномерных шкал S = S = const и S_cp = l/х^ где х^ — диапазон измерений.

Поскольку х и у могут быть выражены в различных единицах, то величина S имеет размерность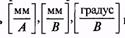и т.д.

Говоря о чувствительности, указывают чувствительность тока, напряжения и т. д.

Иногда для оперирования безразмерными единицами вводят понятие относительной чувствительности

где х₀, у₀ — номинальные (или средние) величины.

Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.

Величину, обратную чувствительности, называют постоянной прибора С= 1/S.

Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.

Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измеренной величины и неизменных внешних условиях: var= х_в — х_у

где х_в, х_у — показания образцового СИ при возрастании и убывании величины х.

Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.

Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы.

Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает отреагировать на это изменение, из-за своих интегрирующих свойств.

По степени полноты описания инерционных свойств средств измерений динамические характеристики делятся на полные и частные.

К полным динамическим характеристикам относятся:

дифференциальное уравнение, описывающее работу средств измерений;

совокупность амплитудной и фазочастотной характеристики.

Частными динамическими характеристиками могут быть отдельные параметры полных динамических характеристик или характеристики, не отражающие полностью динамических свойств средств измерений, но необходимые для выполнения измерений с требуемой точностью (например, время установления показания) или контроля однородности свойств средств измерений данного типа. На эти характеристики средств измерений устанавливаются нормы с целью оценки точности измерений, сравнения средств измерений между собой и выбора из них таких, которые обеспечивают требуемую точность измерений, достижение взаимозаменяемости средств измерений.

Источник

У приборов каких систем шкала неравномерная какими способами устраняется неравномерность шкал

Счётная линейка получила широкое применение в инженерных расчётах, а с повышением технического уровня нашей страны она становится необходимым инструментом не только инженера, но и квалифицированного рабочего.

Устройство счётной линейки основано на теории логарифмов, но для практического пользования линейкой можно обойтись без знания логарифмов.

Для того чтобы в совершенстве овладеть вычислениями на линейке, необходимо непрерывно упражняться и пользоваться ею при всевозможных расчётах на уроках математики, физики, химии, машиноведения, а также в мастерских и вне школы.

§ 85. Равномерные и неравномерные шкалы.

Рассмотрим обыкновенную миллиметровую линейку (черт. 34).

На ней нанесён ряд делений с равными промежутками в 1 мм, вначале стоит цифра 0, а под каждым десятым делением подписаны цифры 1, 2, 3, . 10. Такая миллиметровая линейка представляет пример равномерной шкалы.

Если принять за единицу длины отрезок в 1 см, то в точке а (черт. 35) мы прочтём число 0,8, в точке

в точке Если же положить, что единица выражается длиной не в 1 см, а в 1 мм, то штрих, помеченный цифрой 1, будет уже изображать число 10, и в точке а мы прочтём 8, в точке в точке

Итак, в зависимости от того, какую длину мы принимаем за единицу, значение одного и того же штриха шкалы изменяется.

Так как один и тот же штрих шкалы может обозначать различные числа, отличающиеся друг от друга в раз, то мы часто будем читать числа как цифровой ряд, не обращая внимания на положение запятой и нули в конце числа. Например, числа 6,25; 62,5; 625; 6250; 0,0625 читаются одинаково: — шесть — два — пять.

При помощи двух равномерных шкал можно устроить прибор для сложения и вычитания чисел. На чертеже 36 показано, как на таком приборе найти сумму 14 и 26.

Для того чтобы осуществить это сложение, нужно против 14 на нижней шкале поставить 0 (начало) верхней шкалы, и тогда против 26 верхней шкалы прочтем на нижней

Легко сообразить, как на этом приборе, можно производить вычитание двух чисел.

Но если вместо равномерных шкал воспользоваться специальными неравномерными шкалами, то оказывается возможным производить умножение, деление, возведение в степень и другие действия над числами.

Познакомимся с некоторыми неравномерными шкалами.

На чертеже 37 изображена мерная коническая мензурка, которая кверху расширяется, и расстояния между делениями шкалы постепенно уменьшаются, хотя соответствующие им объёмы жидкости равны. На мензурке мы видим неравномерную шкалу.

На многих электрических приборах можно увидеть неравномерные шкалы, например на амперметре (черт. 38), вольтметре и др. Дальше мы подробно рассмотрим неравномерные шкалы на счётной линейке.

Источник

Большая Энциклопедия Нефти и Газа

Неравномерная шкала

Неравномерная шкала — это большой недостаток прибора, с таким прибором трудно работать, так как очень тяжело оценивать доли делений, если расстояния между делениями различны. [1]

Неравномерные шкалы используются в приборах определенного целевого назначения. На рис. 3.1 изображена шкала неравномерного типа для вольтметра. Вольтметр со шкалой такого типа удобно применять в устройствах, в которых возможны броски напряжения. [2]

Неравномерную шкалу имеют, например, приборы для измерения расхода методом переменного перепада вследствие нелинейной зависимости между величиной перепада и расходом. [4]

Различают равномерные и неравномерные шкалы . Достоинством равномерной является постоянство масштаба вдоль всей шкалы, что обеспечивает простоту отсчета измеряемой величины в любой части шкалы. [5]

На неравномерной шкале ( рис. V-4) цена большого деления равна десяти, а малого — пяти единицам на деление. [7]

При неравномерной шкале чувствительность прибора на различных участках шкалы различна, так как одному и тому же приращению тока будут соответствовать разные отклонения стрелки прибора. [8]

В неравномерных шкалах против отметки, с которой начинается изменение цены деления, число отсчета проставляется независимо от размеров отметки ( фиг. [9]

Реле имеет неравномерную шкалу , про-градуированную от 0 до 60 сек. Минимальная выдержка времени, даваемая реле, равна 2 сек. [11]

Реле имеет неравномерную шкалу , проградуированную от 0 до 60 сек. Минимальная выдержка времени равна 2 сек. Питание реле осуществляется от сети переменного тока частотой 50 гц и напряжением 220 в. Мощность, потребляемая реле, равна 15 ва. [12]

Весы имеют неравномерную шкалу и оснащаются противовесом или пружиной противодавления. [13]

Прибор имеет неравномерную шкалу . Из-за невысокой точности и малой чувствительности применение приборов электромагнитной системы в практике ремонта радиостанций ограничивается измерением тока и напряжения на силовых распределительных щитах. [15]

Источник

Большая Энциклопедия Нефти и Газа

Неравномерная шкала

Иногда бывает удобно применять неравномерные шкалы . Так, часто применяется логарифмическая шкала ( рис. 3), в которой число л1 изображается точкой, полученной откладыванием от некоторой выбранной точки А в положительном направлении отрезка длины k g n, где k — некоторый выбранный коэффициент пропорциональности. [31]

На рис. 4.1 изображена неравномерная шкала . Наименьшее значение измеряемой величины, указанное на шкале, называется начальным значением шкалы дгн. [33]

На рис. 4.1 изображена неравномерная шкала . Наименьшее значение измеряемой величины, указанное на шкале, называется начальным значением шкалы ха. [35]

Электроизмерительные приборы могут иметь равномерные и неравномерные шкалы . На равномерной шкале расстояния между равнозначными делениями равны и чувствительность прибора по всей длине шкалы одинакова. Чувствительность прибора с неравномерной шкалой ( например, амперметр или вольтметр электромагнитной системы) в разных точках шкалы различна. В начале шкалы расстояния между делениями значительно меньше, чем в остальной ее части, что объясняется более низкой чувствительностью прибора при малых токах его рабочего диапазона. [36]

Приборы термоэлектрической системы имеют неравномерную шкалу , близкую к квадратичной. Ее рабочая часть заключена в пределах от 20 до 100 % номинального значения. [37]

Для приборов, имеющих резко неравномерную шкалу , например для омметров, фазометров, приведенная погрешность выражается в процентах от длины шкалы. [38]

Обычные модели рефрактометров Аббе имеют неравномерные шкалы с ценой деления Ы0 — 3 ( иногда 0 5 — 10 — 3); оценка четвертого десятичного знака производится визуальной интерполяцией. Неравномерность шкал п исключает возможность применения нониусов или других приспособлений для более точного объективного отсчета. [39]

Обычные модели рефрактометров Аббе имеют неравномерные шкалы с ценой деления ЫО-3 ( иногда 0 5 — 10 — 3); оценка четвертого десятичного знака производится визуальной интерполяцией. [40]

В лабораторных квадрантных весах применены дуговые неравномерные шкалы . [41]

Величина Рф образует на вертикали неравномерную шкалу . [42]

Электродинамические вольтметры и амперметры имеют неравномерную шкалу . [43]

Механизм должен иметь для и неравномерную шкалу . Применяется для получения произведения сложной функции и простого сомножителя и обладает большей точностью по сравнению с другими типами механизмов. [45]

Источник

Метрологические характеристики средств измерений

Для оценки пригодности СИ к измерениям в известном диапазоне с известной точностью вводят метрологические характеристики (далее — MX) СИ с целью:

• обеспечения возможности установления точности измерений;
• достижения взаимозаменяемости СИ, сравнения СИ между собой и выбора нужных СИ по точности и другим характеристикам;
• определения погрешностей измерительных систем и установок на основе MX входящих в их СИ;
• оценки технического состояния СИ при поверке.

По ГОСТ 8.009—84 устанавливают перечень MX, способы их нормирования и формы представления. Каждая из видов MX по назначению может быть представлена более детально с учетом видов самих измерений и СИ в зависимости от изменений влияющих величин или неинформативных параметров входного сигнала.

Неинформативным называется параметр входного сигнала СИ, не связанный функционально с измеряемым параметром. Например, частота переменного тока при измерении его амплитуды.

Нормальные метрологические характеристики (далее — НМХ) устанавливаются документами. MX, определенные документами, считаются действительными. На практике наиболее распространены следующие MX СИ.

Диапазон измерения— область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования).

Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.

Шкала средств измерения — это упорядоченная совокупность отметок и цифр, соответствующая ряду последовательных значений измеряемой величины.

В шкале Цельсия за начало отсчета принята температура таяния льда, в качестве основного интервала (опорной точки) — температура кипения воды. Одна сотая часть этого интервала — градус Цельсия.

Различают несколько разновидностей шкал:

• шкала наименований — это качественные шкалы, которые не содержат нуля и единиц измерений, здесь присутствуют отношения типа «больше – меньше». Примером может служить шкала цветов (атлас цветов, в графических программах — палитра цветов). Измерение заключается в визуальном сравнении окрашенного предмета с образцами цветов (эталонными образцами атласа цветов). Так как каждый цвет имеет множество оттенков, такое сравнение под силу эксперту, который имеет не только опыт, но и обладает соответствующими особыми характеристиками возможностей визуального наблюдения;
• шкала порядка — свойства величин описывают как отношением эквивалентности, так и отношением порядка по возрастанию или убыванию количественного проявления свойства. В таких шкалах может присутствовать нулевая отметка, но отсутствуют единицы измерения, поскольку невозможно установить, в какое число раз больше или меньше проявляется свойство величины. Обычно шкалы порядка характеризуют значение измеряемой величины (сила ветра, сила землетрясения и т.д.);
• шкала интервалов (разностей). Описывать свойства величин можно не только с помощью отношений эквивалентности и порядка, но и с применением суммирования и пропорциональности интервалов (разностей) между количественными проявлениями данного свойства. Шкалы интервалов имеют условные нулевые значения, а интервалы устанавливаются по согласованию. Такими шкалами являются шкалы времени и длины;
• шкала отношений имеет естественное нулевое значение, а единица измерений устанавливается по согласованию. Например, шкала весов, начинаясь с нулевой отметки, может быть проградуирована по-разному в зависимости от требуемой точности взвешивания;
• абсолютные шкалы всегда имеют определение единицы измерения ФВ;
• условные шкалы — это шкалы ФВ, исходные значения которых выражены в условных единицах, иногда их называют несимметричными. К ним относят шкалы твердости минералов и металлов.

Различают равномерные и неравномерные шкалы. Последние делятся на существенно неравномерные и степенные. Под существенно неравномерной шкалой понимают шкалу с сужающимися делениями, на которой отметка, соответствующая полусумме начального и конечного значения рабочей части шкалы, расположена между 65 и 100 % длины этой рабочей части. Под степенной шкалой понимают шкалу с расширяющимися или сужающимися делениями, но не попадающими под определение существенно неравномерных.

Например, у шкалы на рис.3.6 начальный участок (

20 %) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10. 50 ед.

Рис. 3.6. Неравномерная шкала СИ

Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.

Чувствительность — отношение изменения сигнала dу на выходе СИ к вызвавшему это изменение изменению dх сигнала на входе:

S = dу/dх. (3.2)

Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины:

S= dl/dx.(3.3)

Таким образом, для неравномерных шкал величина S = var, и степень неравномерности шкалы оценивают через коэффициент: J = S_max/S_min.

Для равномерных шкал
S=S_ср = const иS_ср =l/x_n, (3.4)
где x_n— диапазон измерений.

Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.

Величину, обратную чувствительности, называют постоянной прибораC=1/S.

Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления. Поэтому для СИ с неравномерной шкалой чувствительность — величина переменная.

Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:

H=|xв –xу| (3.5)

где xв, xу — значения измерений образцовыми СИ при возрастании и убывании величины x. Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.

Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы. Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изучении тока подвижная часть СИ, вследствие инерции, не успевает « следить» за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.

Точность измерения — это степень приближения результатов измерения к некоторому действительному значению физической величины. Чем меньше точность, тем больше погрешность измерения и, соответственно, чем меньше погрешность, тем выше точность.

Класс точности — это обобщенная метрологическая характеристика, определяющая различные свойства средств измерения. Например, у показывающих электроизмерительных приборов класс точности помимо основной погрешности включает вариацию показаний, а у мер электрических величин – величину нестабильности (процентное изменение значение меры в течение года). Класс точности уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерения, выполняемых с помощью этих СИ, поскольку точность измерения зависит от метода измерения, взаимодействия СИ с объектом, условий измерений и т.д. В частности, для того чтобы измерить величину с точностью до 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, так как нужно учесть как минимум еще погрешность метода. Определяя класс точности, нормируют прежде всего пределы допускаемой основной погрешности d_осн . В связи с большим разнообразием как самих СИ, так и их МХ, ГОСТ 8.401— 80 устанавливает несколько способов назначения классов точности.

Основная MX СИ — погрешность СИ — есть разность между показаниями СИ и истинными (действительными) значениями ФВ.

Классификация погрешностей СИ:

по отношению к внешним воздействиям:

• основная
  • от внешних факторов
  • от внутренних факторов
• дополнительная
  • случайная
    • нестабильность режима работы объекта
    • электромагнитные наводки
    • неинформативные параметры процесса
    • изменение свойств линии связи измерительных калибров
    • сбои
    • колебание параметров источников питания
  • прогрессирующая
    • от температуры
    • от влаги
    • от давления
    • от вибрации и ударов

по способу выявления:

• случайная
• систематическая
  • методическая
    • косвенного измерения
    • передачи размера
    • квантования по уровню и времени
    • вычисления
    • алгоритма контрольных операций
  • инструментальная
    • воздействия СИ на объект
    • конечной разрешающей способности
    • нормированная погрешность СИ
  • постоянная
  • периодическая

по характеру режима измерения:

• статическая
• динамическая
  • периодических процессов (амплитудная, фазовая, частотная)
  • переходных процессов

по способу нормирования МХ:

по взаимодействию с выходным сигналом:

Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.

Основная погрешность — это погрешность СИ при нормальных условиях эксплуатации. Как правило, нормальными условиями эксплуатации являются: температура 293 ± 5 К или 20 ± 5 °С, относительная влажность воздуха 65 ± 15 % при 20 °С, напряжение в сети питания 220 В ±10 % с частотой 50 Гц ±1 %, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).

В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ.

Существуют три способа нормирования основной погрешности СИ:

• нормирование пределов допускаемой абсолютной (±D) или приведенной (± у) погрешностей, постоянных во всем диапазоне измерения;
• нормирование пределов допускаемой абсолютной (±D) или относительной (±s) погрешностей в функции измеряемой величины;
• нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков.

В качестве предела допускаемой погрешности выступает наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению. То же самое относится и к дополнительным погрешностям. При этом исходят из следующих положений:

• дополнительная погрешность имеет такой же вид, что и основная (абсолютная, относительная и приведенная);
• дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно.

Иногда дополнительную погрешность нормируют в виде коэффициента, указывающего, «на сколько» или «во сколько» изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10 °С, означает, что при изменении среды на каждые 10 °С добавляется дополнительная погрешность 1 %.

Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).

Случайной погрешностью СИ называют составляющую, изменяющуюся при повторных измерениях одной и той же величины случайным образом (например, вызванные неправильным функционированием механических или электрических элементов измерительного устройства).

Систематическая погрешность СИ — это составляющая общей погрешности, которая остается постоянной или закономерно изменяется при многократных измерениях одной и той же величины (например, если тензосопротивление (изменяется сопротивление от приложенного давления)* плохо наклеено на упругий элемент, то деформация его решетки не будет соответствовать деформации упругого элемента и датчик будет постоянно неправильно реагировать). Различают следующие составляющие систематической погрешности:

• методическая — обусловлена несовершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов,
• инструментальная — возникает из-за собственной погрешности средств измерения, определяемой классом точности, влиянием средств измерения на результат и ограниченной разрешающей способности средств измерения,
• постоянная
• периодическая.

Выделяют также грубые погрешности которые, как правило, допускаются самим исполнителем, который из-за неопытности или усталости неправильно считывает показания приборов или ошибается при обработке информации. Их причиной могут стать и неисправность средств измерения, и резкое изменение условий измерения.

Статистические погрешности возникают при измерении постоянных величин после завершения переходных процессов в элементах СИ.

Динамическая погрешность — разница между погрешностями СИ в динамическом режиме и его статистической погрешностью.

В соответствии с ГОСТ 8.401—80 для пределов допускаемой основной (и дополнительной) погрешностей предусмотрены различные способы выражения в виде абсолютной, относительной и приведенной погрешности.

Абсолютная погрешность — разность между показаниями x СИ и действительным значением x_д измеряемой величины. Выражается она в единицах измеряемой ФВ и может быть задана:

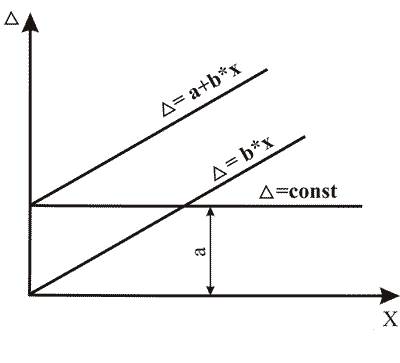
• одним числом D = ± a — аддитивная погрешность или погрешность нуля (неизменна во всем диапазоне измерения);
• в виде линейной зависимости D = ± (a +bx ) — мультипликативная погрешность (изменяется пропорционально);
• в виде функции D = f(x), графика или таблицы — присутствует аддитивная и мультипликативная составляющие (рис. 3.7);

Рис. 3.7. Формирование аддитивной и мультипликативной
составляющих погрешности

Поскольку абсолютная погрешность выражается в абсолютных единицах ФВ, то это не дает возможность сравнивать СИ и измеряющие разные ФВ. Для этой цели можно использовать относительные погрешности D как отношение абсолютной погрешности к действительному x_д значению, выраженные в процентах

d= ± ( D /x_д) · 100 %.(3.6)

Эта формула показывает, что для одного и того же СИ d уменьшается с ростом x_д и приближается к бесконечности (¥) при x_д ®0. То есть при измерении на начальном участке шкалы с начальной нулевой отметкой погрешности измерения могут быть сколь угодно велики. Поэтому в метрологии существует принцип запрета измерений на таких участках.

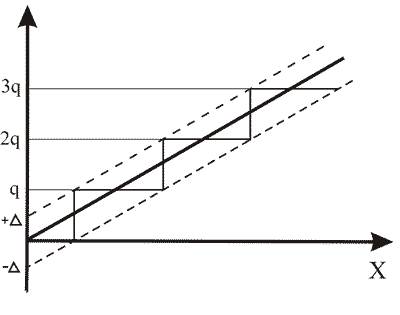
Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения на рис.3.8 приведена текущая разность (погрешность квантования) номинальной (линия 1) и реальной (линия 2) характеристик цифрового СИ в полосе (штриховые линии) погрешностей. Поскольку измеряемая величина x может принимать случайные значения в интервале от от +D до –D , то погрешность квантования есть случайная аддитивная статическая погрешность. Она не зависит ни от текущего значения х, ни от скоростей измерения х во времени. На рисунке 3.8 величина q — шаг квантования по уровню.

Рис. 3.8. Квантование погрешности цифровых СИ

При многократных измерениях в качестве истинного значения, как правило, используют среднее арифметическое значение.

Калибровка средств измерения

Калибровка средства измерения — совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и (или) пригодности к применению средства измерения, не подлежащего государственному метрологическому контролю и надзору (далее — ГМНиК).

Из определения можно сделать два вывода:

• калибровка проводится для тех СИ, которые не используются в сферах ГМКиН (установленных ст. 13 Закона РФ от 27.04.93 № 4871—1 «Об обеспечении единства измерений»), а значит, не подлежат поверке;
• калибровка выполняет две функции:
  • определение и подтверждение действительных значений метрологических характеристик СИ;
  • определение и подтверждение пригодности СИ к применению.

В первом случае лаборатория, калибрующая по заявке (договору) заказчика СИ, не делает вывода о пригодности прибора. Установленные характеристики могут отличаться от паспортных, и только в компетенции заказчика определять, в каких условиях и для каких целей можно и нужно использовать данные СИ.

Во втором случае СИ признается пригодным, если действительное значение его метрологических характеристик соответствует техническим требованиям, установленным в НД или заказчиком. Вывод о пригодности СИ в этом случае делает калибровочная лаборатория.

В решаемых на практике измерительных задачах калибровка может сводиться только к проверке пригодности СИ, т.е. его работоспособности. В частности, требуется знать не действительные значения измеряемой величины, нужно лишь констатировать наличие величины измеряемого сигнала определенного уровня. Примером может служить калибровка устройств — сигнализаторов предельного значения температуры. В сигнализаторах, имеющих одну или несколько сигнальных лампочек, включение или выключение последних свидетельствует о достижении предельных значений величины. В устройствах, имеющих шкалу в виде нескольких цветовых секторов (подобных посуде фирмы «Цептер»), положение указательной стрелки в пределах конкретного сектора означает определенное состояние объекта измерений.

Калибровка может быть возложена как на МС юридического лица, так и на любую другую организацию, способную выполнить калибровочные работы.

Результаты калибровки СИ удостоверяются калибровочным знаком, наносимым на СИ, записью в эксплуатационных документах или сертификатом о калибровке.

На основе договоров, заключаемых с государственными научными метрологическими центрами или органами ГМС, заинтересованные МС юридических лиц могут быть аккредитованы на право проведения калибровочных работ. В этих случаях последним предоставляется право выдавать сертификаты о калибровке от имени органов и организаций, которые их аккредитовали.

Аккредитация — процедура добровольная. В каких случаях она необходима? Прежде всего, тогда, когда предприятие поставляет продукцию на зарубежные рынки. В этом случае торговый партнер (покупатель) может потребовать от продавца подтверждения того, что характеристики продукции измерялись приборами, проверенными аккредитованной МС.

В 1994—1995 гг. в России сформировалась Российская система калибровки (РСК). В «Положении о Российской системе калибровки» регламентированы следующие вопросы:

• организация, структура и функции РСК;
• права и обязанности входящих в нее юридических лиц независимо от форм собственности и пр.

Источник