У англичан принято давать детям несколько имен сколькими способами можно назвать ребенка 300

Решение комбинаторных задач

Презентация на тему : » Решение комбинаторных задач «.

Просмотр содержимого документа
«Решение комбинаторных задач»

Решение комбинаторных задач

Выполнила: ученица 9Б класса МБОУ «СОШ № 47» Советского р-на города Казани Николаева Светлана Андреевна 2017-2018 учебный год

• Это раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана с другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).

• Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег , 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег.

У мамы m яблок и n груш. Каждый день в течение пяти дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

• Имеем набор <я, я, г, г, г>. Всего перестановок пятиэлементного множества
• 5, но мы не должны учитывать перестановки, в которых объекты одного типа меняются
• местами несколько раз, поэтому нужно поделить на возможное число таких перестановок:
• 2 · 3. Получаем в итоге
• 5/2*3=3*4*5/2*3=10 Ответ: 10 способов.

Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?

Пронумеруем места в купе (с № 1 по № 4) и будем «выдавать» каждому из трех членов семьи номер места. Из 4 элементов (номе­ров мест) будут делаться выборки по 3 элемента, при этом важен не только состав выборки, но и порядок расположения в ней элемен­тов (кто именно и на каком месте поедет). Число способов равно числу размещений из 4 по 3:

Можно рассуждать, непосредственно применяя правило произ­ведения: для первого члена семьи можно выбрать любое из 4 мест, для второго — любое из 3 оставшихся, для третьего — любое из двух оставшихся, всего 4*3*2 = 24 способа рассадить семью в купе.

Ответ: 24 способа.

Сколькими способами можно расставить на полке 8 различных книг?

8! = 1*2*3*4*5 6*7*8= 40320. Ответ:40320

Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A7^3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

• Ответ: 210.

У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имел равно 300, а ему дают не более трех имен?

Решение. 1) если выбрали одно имя то количество способов его выбрать = 300

2) если два имени:

300!/(2!*(300-2)!)=44850 (комбинация из 300 по 2)

300!/(3!*(300-3)!)=4455100 (комбинация из 300 по 3)

Ответ: 4500250 способов

Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A107 – A96 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320

В урне лежат 10 жетонов с числами 1,2,3, . 10. Из нее, не выбирая, вынимают 3 жетона. Во скольких случаях сумма написанных на них чисел не меньше 9

• Решение. Неблагоприятные исходы: (1,2,3), (1,2,4), (1,2,5), (1,3,4) (в этих случаях сумма чисел меньше 9). Всего исходов . Значит, всего благоприятных исходов С3\10. С3\10 – 4=120 – 4=116

Ответ: в 116 случаях

На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, и с сыром и с колбасой – 28 человек; и с колбасой и с ветчиной – 31 человек, и с сыром и с ветчиной – 26 человек. Все три вида бутербродов взяли 25 человек, а несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?

Решение задачи становится очевидно, если описать условие с помощью диаграммы Венна (в виде пересекающихся кругов, изображающих множества), приняв следующие обозначения:

• А — множество туристов, которые взяли с собой бутерброды с колбасой;
• В — множество туристов, которые взяли с собой бутерброды с сыром;
• С — множество туристов, которые взяли с собой бутерброды с ветчиной.
• Начертим диаграмму…
• На этой диаграмме видно:
• а) Количество туристов, взявших с собой бутерброды всех трех видов (25).
• б) Количество туристов, взявших с собой бутерброды каких-либо двух видов (с учетом туристов, взявших с собой бутерброды всех трех видов) – соответственно 3, 1 и 6 человек (чтобы общее число этих людей в соответствии с условием было равно 28, 26 и 31 человек).
• в) Количество туристов, взявших с собой бутерброды какого-либо одного вида (с учетом туристов, перечисленных в пунктах а и б) – соответственно 13, 9 и 10 человек (чтобы общее число этих людей в соответствии с условием было равно 47, 38 и 42 человека).
• Тогда общее число любителей бутербродов составит 25 + 3 + 1 + 6 + 13 + 9 + 10 = 67 человек, Следовательно, пирожки взяли с собой 92 – 67 = 25 человек.

Имеется 6 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну — на правую так, чтобы выбранные перчатки были разных размеров?

• На левую руку можно выбрать любую из 6 перчаток на левые руки. На правую – любую из пяти перчаток на правую руку. Значит, всего способов 6 * 5=30.

Ответ: 30 способов

На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?

Решение. Собираем все варианты в таблицу.

• Булочка (Б)Ватрушка (В)Пирожок (П)Сок (С)Чай (Ч)
• В таблице 2 строки и 3 столбца, которые образуют 6 клеток. Так как выбор еды и напитка происходит независимо, то в каждой клетке будет стоит один из возможных вариантов завтрака. Значит, всего вариантов столько, сколько клеток в таблице, то есть 6. Напиток можно выбрать двумя способами (сок или чай), а еду тремя способам.

2 ∙ 3 = 6 столовая предлагает 6 вариантов завтрака.

Ответ : 6 способов

Из города А в город В ведут пять дорог, а из города В в город С — три дороги. Сколько путей, проходящих через В, ведут из А в С?

• Представим задачу в виде графа. Очевидно, что какой бы путь не выбрал объект, продвигаясь из пункта А в пункт В, по достижении пункта В он может выбрать любой из трех путей, позволяющих ему добраться из В в С.

Следовательно, путей, ведущих из А в С и проходящих через В, существует 5 * 3 = 15. Ответ : 15 способ

В купе железнодорожного вагона имеются два противоположных дивана по 5 мест на каждом. Из 10 пассажиров этого купе четверо желают сидеть лицом к паровозу, 3 – спиной к паровозу, а остальным безразлично как сидеть. Сколькими способами могут разместиться пассажиры с учетом их желаний?

• Разместим четверых желающих пассажиров лицом к паровозу (на 5 местах). Это можно сделать А способами, разместим троих желающих пассажиров спиной к паровозу. Это можно А сделать способами, Осталось 3 «безразличных» пассажира и для них 3 места. Их можно разместить 3 способами. Значит, всего способов размещения А*А=43200.

Ответ: 43200 способов

В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток? Сколькими способами можно купить 8 открыток? Сколькими способами можно купить 8 различных открыток?

число сочетаний из 10 по 8

В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?

Выберем любой из 15 комплектов предыдущей задачи. Его можно дополнить ложкой четырьмя различными способами. Поэтому общее число возможных комплектов равно 60 (60 = 15 • 4 = 5 • 3 • 4). Ответ : 60 способов

Источник

Элементы комбинаторики

Несколько задач по комбинаторике. Общие правила комбинаторики. Комбинаторика в вероятностных задачах.

Просмотр содержимого документа
«Элементы комбинаторики»

Автор –составитель :Паньковская Юлия Вадимовна

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучают закономерности создания подобных комбинаций, называется комбинаторикой.

Комбинаторика возникла в XVI веке. В то время в жизни общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, насколько часто можно выбросить данное число очков, бросая две или три кости, или получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и теории вероятностей.

Большим подспорьем для математиков являлось то, что решения задач такого рода можно было проверить на практике – во время игр. Зачастую проходило так, что во время многочасовых игр замечались определенные закономерности (например, что определенные комбинации карт или костей появляются чаще других), о которых игроки сообщали математикам, а последние объясняли эти наблюдения.

Одним из первых занялся подсчетом различного числа комбинаций при игре в кости итальянский математик Никколо Тарталья (ок.1499 -1557). Дальнейшее развитие комбинаторики связано с именами Блеза Паскаля (1623 – 1662), Пьера Ферма (1601 -1665), Якоба Бернулли (1654 -1705), Готфрида Вильгельма Лейбница (1646 -1716) и Леонарда Эйлера (1707 -1783). Однако у них основную роль играли приложения к различным играм (лото, солитер и др.), а также большое количество занимательных задач и головоломок. Долгое время казалось, что комбинаторика лежит вне основного русла развития математики и ее приложений.

Положение резко изменилось после появления во второй половине ХХ века электронных вычислительных машин и связанного с этим расцветом дискретной математики. С этого момента комбинаторика переживает период бурного развития. Комбинаторные методы находят множество применений. Они используются для решения транспортных задач (в частности задач по составлению расписаний), для составления планов производства и реализации продукции, в теории случайных процессов, статистике, вычислительной математике, планировании экспериментов, шахматных программах для ЭВМ и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории кодирования и теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах – при изучении конечных геометрий, теории групп и их представлений, неассоциативных алгебр и т.д.

ОБЩИЕ ПРАВИЛА КОМБИНАТОРИКИ

«Опять восьмерка!» — горестно воскликнул председатель клуба велосипедистов, взглянув на погнутое колесо своего велосипеда. «А все почему? Да потому, что у меня членский билет №088 – по восьмерке на каждое колесо! И теперь не проходит и месяца, чтобы то на одном, то на другом колесе не появилась восьмерка. Надо менять номер билета! А чтобы меня не обвинили в суеверии, проведу перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые ни одна восьмерка не входит. Не знаю только, хватит ли на всех номеров – ведь у нас в клубе почто 600 членов, а номера должны быть трехзначными. Неужели придется выписывать все номера от 000 до 999, а затем вычеркивать из них все номера с восьмерками?»

Попробуем помочь председателю. Нам нужно решить такую комбинаторную задачу: сколько трехзначных номеров, не содержащих цифры 8?

Для решения этой задачи определим сначала, сколько однозначных номеров не содержит цифру 8. Ясно, что таких номеров девять: 0, 1, 2, 3, 4, 5, 6, 7, 9. А теперь найдем все двузначные номера, не содержащие цифру 8. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится девять двузначных. А так как однозначных номеров тоже девять, то получиться 9·9=9 2 двузначных номеров без цифры 8.

За каждым из них снова можно поставить любую из девяти допустимых цифр. В результате получим 9 2 ·9=9 3 =729 трехзначных номеров, не содержащих цифру 8. Значит, таких членских билетов хватит на 729 членов клуба.

А если взять не трехзначные, а четырехзначные номера, то номеров, не содержащих цифру 8, будет 9 4 =6561, а пятизначных – 9 5 =59049.

Заместитель председателя был еще суевернее. Так как число 0 похоже на вытянутое колесо, он предложил отказаться и от этой цифры и попробовать обойтись восемью цифрами: 1, 2, 3, 4, 5, 6, 7, 9. А это у него получится, потому что эта задача похоже на решенную выше, только вместо девяти цифр у нас всего восемь. Поэтому и в ответе надо заменить 9 на 8, так что трехзначных номеров билетов, не использующих цифры 0 и 8, существует 8 3 =512, а членов клуба почти 600.

Зоя Петровна и ее дочь Нина часто играли в лото. Каждая брала по три карточки, Нина хорошо перемешивала бочонки в мешке, затем доставала из мешка очередной бочонок с числом (от 1 до 90), называла его, и тот, у кого на карточке обнаруживалось это число, закрывал его бочонком.

Играли они часто, помнили, как начинались многие игры (кто первым и какой брал себе бочонок), уже не раз первым попадался один и тот же бочонок, но первые два бочонка каждый раз извлекались другие. И однажды Нина задумалась – много ли способов извлечь один за другим два бочонка из мешка, если в нем 90 бочонков?

Первый можно извлечь 90 способами – это понятно, а дальше? Ведь если бочонок 28 уже извлечен, то второй раз его извлечь нельзя. Но Нина как раз в это день готовила таблицу первенства школы по баскетболу, в которой клетки по диагонали перечеркивались (ведь играть сама с собой команда не может), и сообразила, что тот же метод годится и здесь. Она представила себе таблицу 9090, в которой слева написаны возможные номера (от 1 до 90) бочонка, извлеченного первым, а сверху – возможные номера бочонка, извлеченного вторым.

Тогда каждая клетка задает один вариант выбора двух бочонков, вот только клетки диагонали надо зачеркнуть (дважды один бочонок извлечь нельзя).

В этой таблице 90·90=8100 клеток 90 зачеркнуты, значит, остается 8010 вариантов. Это и есть число способов извлечь один за другим два бочонка из 90.

А затем Нина сообразила, что можно рассуждать иначе. Первый бочонок можно извлечь 90 способами. После этого в мешке останется 89 бочонков, правда, каких – зависит от того, какой бочонок извлечен первым. Но способов извлечь второй бочонок всегда будет 89 для каждого из 90 способов извлечь первый бочонок, а всего способов будет 90·89=8010.

«Команда космического корабля»

В случае, когда число возможных выборов на каждом шагу сложным образом зависит от того, какие элементы были выбраны ранее, удобно изображать процесс составления комбинаций в виде «дерева». Сначала из данной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу (таким образом, каждый отрезок соответствует одному элементу). Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если в первый раз был выбран данный элемент, и т.д.

В результате такого построения получатся «дерево», рассмотрение которого дает число решений нашей задачи.

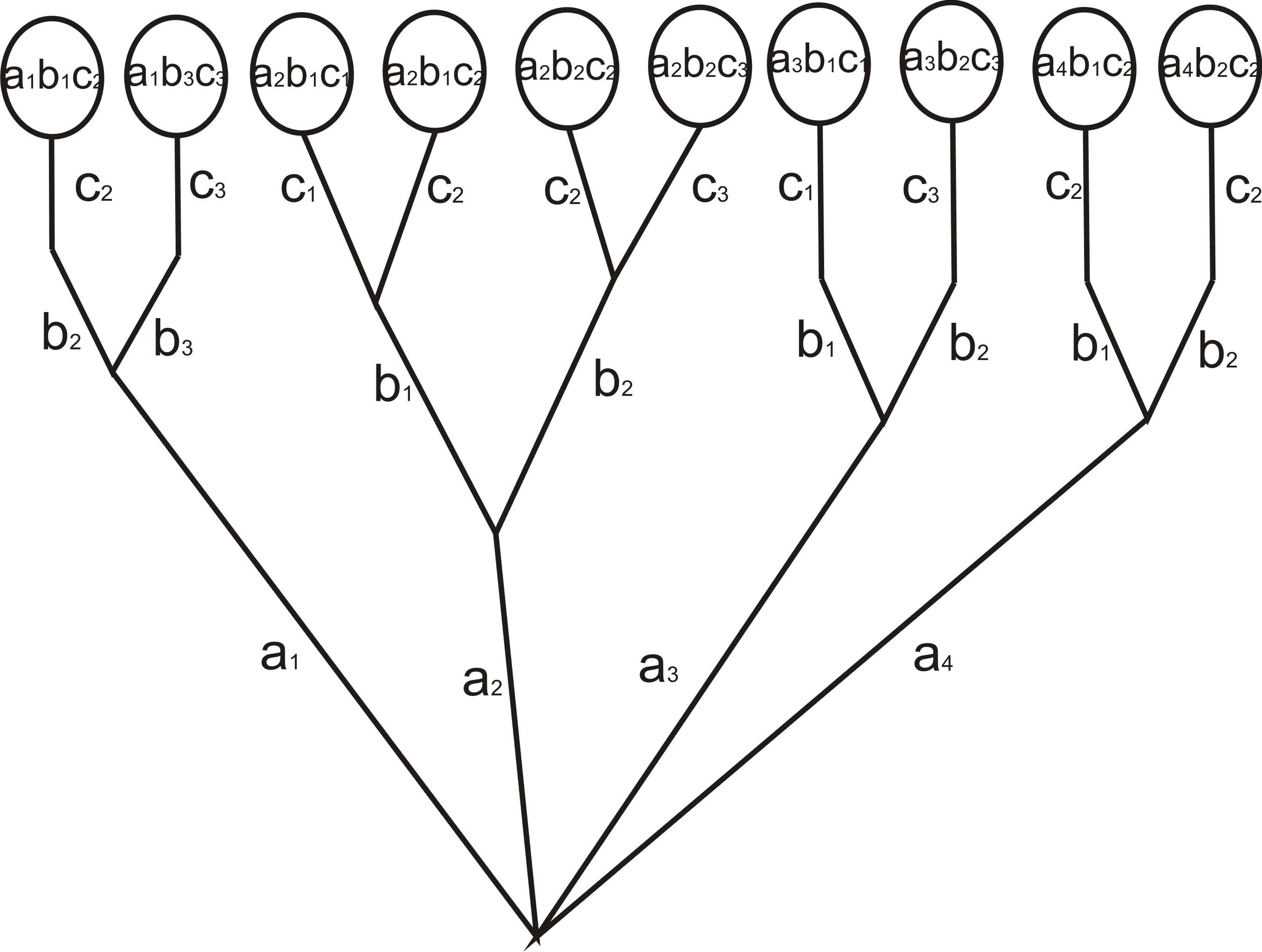
Рассмотрим следующий пример. Известно, что при составлении команд многоместных космических кораблей возникает вопрос о психологической совместимости участников космического путешествия. Даже вполне подходящие порознь люди могут оказаться непригодными для длительного совместного путешествия. Предположим, что надо составить команду космического корабля из трех человек: командира, инженера и врача. На место командира есть четыре кандидата: а₁, а₂, а₃, а₄; на место инженера – 3 кандидата: b₁, b₂, b₃ и на место врача – тоже 3 кандидата: с₁, с₂, с₃. Проведенная проверка показала, что командир а₁ психологически совместим с инженерами b₁ и b₃ и врачами с₂ и с₃; командир а₂ – с инженерами b₁ и b₂ и всеми врачами; командир а₃ – с инженерами b₁ и b₂ и врачами с₁, с₃; командир а₄ – со всеми инженерами и врачом с₂. Кроме того, инженер b₁ психологически несовместим с врачом с₃, инженер b₂ – с врачом с₁ и инженер b₃ – с врачом с₂. Сколькими способами при этих условиях может быть составлена команда корабля?

Соответствующее дерево изображено на рис.1.

Оно показывает, что есть лишь 10 допустимых комбинаций. При этом после каждого выбора командира а_i у нас есть 2 варианта выбора инженера b_j, поэтому появляется 8 пар командир-инженер, а дальше для каждой такой пары в 6 случаях врач c_k определен единственным образом (в силу требований совместимости), а в 2 случаях есть выбор из двух врачей.

Если бы не было ограничения совместимости, то после каждого из 4 возможных способов выбора командира a_i у нас было бы 3 варианта выбора инженера b_j, а затем по 3 варианта выбора врача c_k, и комбинаций было бы 4·3·3=36.

Задача 1. Крыса бежит по лабиринту, который устроен так, что сначала она должна выбрать одну из двух дверей, затем одну из трех дверей, а за каждой из них ее ожидают четыре двери. Пройдя какую-либо дверь, крыса не может вернуться через нее обратно. Сколькими различными путями крыса может пройти лабиринт?

Задача 2. Сколькими способами можно прочитать слово КРОНА в таблице, начиная с буквы К в левом верхнем углу и двигаясь вправо или вниз до последней буквы?

Источник