ТУПИКОВЫЕ И СОКРАЩЕННЫЕ ДНФ. ГЕОМЕТРИЧЕСКИЕ И АНАЛИТИЧЕСКИЕ МЕТОДЫ ИХ ПОСТРОЕНИЯ
Описание: Теорема. Пусть – произвольная булева функция () и – ее произвольная тупиковая ДНФ Тогда существует такое упорядочение совершенной ДНФ, из которого при помощи алгоритма упрощения получается тупиковая ДНФ .
Дата добавления: 2015-01-30
Размер файла: 147.98 KB
Работу скачали: 63 чел.
Поделитесь работой в социальных сетях
Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск
аранов Виктор Павлович. Дискретная математика. Раздел 5. ДНФ и схемы из ФЭ.
Лекция 225-26. Т упиковые и сокращенные ДНФ . Геометрические и аналитические методы их построения
Лекция 25-26. ТУПИКОВЫЕ И СОКРАЩЕННЫЕ ДНФ.
ГЕОМЕТРИЧЕСКИЕ И АНАЛИТИЧЕСКИЕ МЕТОДЫ ИХ ПОСТРОЕНИЯ
1. Определение тупиковой ДНФ.
2. Построение тупиковых ДНФ методом упрощения совершенной ДНФ.
3. Определение сокращенной ДНФ и геометрический метод ее построения.
4. Аналитические методы построения сокращенной ДНФ.
5. Построение тупиковых ДНФ на основе геометрических представлений.
- Определение тупиковой ДНФ
Пусть произвольная ДНФ, которую можно представить следующим образом:
Здесь элементарная конъюнкция из , ДНФ, образованная из остальных конъюнкций, входящих в ; некоторый множитель из ; произведение остальных множителей из .
Рассмотрим два типа преобразования ДНФ.
- Операция удаления элементарной конъюнкции. Переход от ДНФ к ДНФ преобразование, осуществляемое путем удаления элементарной конъюнкция . Данное преобразование определено тогда и только тогда, когда .
- Операция удаления множителя . Переход от ДНФ к ДНФ преобразование, осуществляемое путем удаления множителя . Данное преобразование определено тогда и только тогда, когда .
ДНФ , которую нельзя упростить при помощи преобразований I и II , называется тупиковой ДНФ. ( ТДНФ ).
Например, очевидно, что ДНФ будет тупиковой.
- Построение тупиковых ДНФ методом упрощения совершенной ДНФ
Рассмотрим алгоритм упрощения ДНФ, приводящий к тупиковой ДНФ Отметим, что среди тупиковых ДНФ всегда содержатся и минимальные, но не все.
1 . Для функции выбирается в качестве исходной какая-нибудь ДНФ Таковой можно взять, например, совершенную ДНФ, так как существует простой способ ее построения.
2 . Осуществляется упорядочивание в исходной ДНФ слагаемых и в каждом слагаемом множителей. Это упорядочение можно задать записью ДНФ.
3 . Производится просмотр записи ДНФ слева направо. Для очередного члена сначала пробуют применить операцию удаления элементарной конъюнкции . Если это невозможно, то просматривают члены конъюнкции слева направо и применяют операцию удаления множителя до тех пор, пока это удается.
Затем переходят к следующей элементарной конъюнкции. После обработки последней элементарной конъюнкции еще раз просматривают полученную ДНФ слева направо и пробуют применить операцию удаления элементарной конъюнкции. В результате получаем ТДНФ.
Пример1. Рассмотрим функцию . В табличной форме:
В качестве исходной ДНФ выберем совершенную ДНФ
рассмотрим ее упорядочение и проследим работу алгоритма.
1 . Конъюнкция не может быть удалена, но можно удалить множитель :
2 . Конъюнкция не может быть удалена, но можно удалить множитель :
3 . Конъюнкция , может быть удалена так как
4 . Конъюнкция также может быть удалена (см. п. 1 ).
5 . Конъюнкцию удалить нельзя, но можно удалить множитель :
6 . Конъюнкцию удалить нельзя, но можно удалить множитель :
В результате получаем тупиковую ДНФ:
Если для той же функции взять другую упорядоченность ее совершенной ДНФ, например,
то в результате работы алгоритма упрощения получим другую тупиковую ДНФ:
Из приведенного примера следует, что результат применения алгоритма упрощения зависит от выбора упорядочения исходной ДНФ, причем получаемые тупиковые ДНФ имеют различную сложность. В данном случае , .
Таким образом, тупиковые ДНФ могут имеют различную сложность и, в частности, могут отличаться от минимальных. В связи с этим возникает вопрос: возможно ли для любой функции , исходя из некоторого упорядочения, получить, применяя алгоритм упрощения, минимальную ДНФ? Ответ на этот вопрос дает следующая теорема.
Теорема. Пусть произвольная булева функция () и ее произвольная тупиковая ДНФ Тогда существует такое упорядочение совершенной ДНФ, из которого при помощи алгоритма упрощения получается тупиковая ДНФ .
Следствие. В силу того, что среди тупиковых ДНФ содержатся обязательно и минимальные, алгоритм упрощения при надлежащем выборе упорядочения совершенной ДНФ позволяет находить и минимальные ДНФ.
Замечание. Из доказательства этой теоремы, которое мы опускаем, следует, что для построения всех тупиковых ДНФ при помощи алгоритма упрощения из совершенной ДНФ достаточно при естественном порядке конъюнкций варьировать только порядок множителей в конъюнкциях.
Таким образом, для построения минимальной ДНФ следует на основе алгоритма упрощения , варьируя только порядком множителей в конъюнкциях, найти все тупиковые ДНФ.
Выполним оценку трудоемкости такой процедуры минимизации.
Однократное применение алгоритма упрощения содержит проверок возможности удаления конъюнкции, проверок возможности удаления множителя из и при вторичном просмотре не более проверок возможности удаления конъюнкций, то есть
Общее число упорядочения с учетом замечания, равно , причем
Это число меньше, чем , то есть этот алгоритм лучше, чем алгоритм перебора всех ДНФ, но все же он остается весьма трудоемким.
- Определение сокращенной ДНФ и геометрический метод ее построения
Грань , содержащаяся в , называется максимальной , если не существует грани такой, что:
- ;
- Размерность грани больше размерности грани .
Пример 2. Пусть (см. пример 1). Рассмотрим конъюнкции , , , которым соответствуют грани
Эти грани имеют соответственно ранги , , и являются соответственно одномерной гранью (ребром), одномерной гранью (ребром) и двумерной гранью, которые представлены на рис. 1.
Грани и максимальные, а грань не максимальная для , так как и размерность больше размерности .
Конъюнкция , соответствующая максимальной грани множества , называется простой импликантой функции .
Из простой импликанты функции нельзя удалить ни одного множителя, иначе мы получим конъюнкцию , грань которой не содержится в .
Из определения следует, что любую ДНФ, в которой хотя бы один из членов не является простой импликантой, можно упростить. Отсюда следует следующее утверждение.
Теорема. Минимальная ДНФ функции состоит из простых импликант.
ДНФ, являющаяся дизъюнкцией всех простых импликант, называется сокращенной .
Пусть множество всех максимальных граней множества . Тогда
так как и каждая точка из принадлежит некоторой максимальной грани. Последнее равенство эквивалентно следующему :
Так как сокращенная ДНФ реализует функцию , то она имеет вид
Источник
Тупиковая ДНФ. ДНФ Квайна
Построение сокращенной ДНФ является первым шагом в процессе получения минимальной ДНФ. Следующий шаг минимизации – это построение, так называемых, тупиковых ДНФ.
Дадим определение тупиковой ДНФ:
Покрытие множества Nf максимальными гранями называется неприводимым, если совокупность этих граней, получающаяся из исходной путем выбрасывания какой-либо грани, не будет уже покрытием Nf .
ДНФ, которая соответствует неприводимому покрытию, называется тупиковой ДНФ.
Минимальная ДНФ содержится среди тупиковых.
Тупиковые ДНФ получаются путем выбрасывания из сокращенной ДНФ некоторых простых импликант.
Существуют алгоритмы, при помощи которых получаются единственные для данной функции тупиковые ДНФ. К таким тупиковым ДНФ относится ДНФ Квайна.
Введем сопутствующие понятия.
Ядровая грань: максимальная грань называется ядровой, если ей принадлежит вершина, принадлежащая покрытию Nf только этой грани и не принадлежащая никакой другой максимальной грани.
Множество всех ядровых граней покрытия Nf , называется ядром Nf .
Теперь познакомимся с определением ДНФ Квайна:
ДНФ, которую получают путем выбрасывания всех простых импликант, соответствующих максимальным граням, которые покрываются ядром, называется ДНФ Квайна.
Алгоритм построения ДНФ Квайна:
1. получить сокращенную ДНФ;
2. найти ядровые грани;
3. удалить импликанты, покрываемые ядром.
Полученная ДНФ, является ДНФ Квайна.
В предыдущем примере Nk3 – не является ядровой гранью, т.к. каждая вершина принадлежит другим граням. Тогда сокращенную ДНФ можно еще раз минимизировать, выбросив конъюнкцию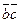 
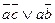
, получим ДНФ Квайна : 
.
Оставшиеся грани Nk1 и Nk2 покрывают Nf . Продемонстрируем это на рисунке:
Отметим справедливость следующего утверждения:
Для любой не тождественно ложной функции существует единственная ДНФ Квайна.
Задачи для самостоятельного решения.
1. Минимизировать функцию, принимающую значение 1, если большинство переменных равны 1, методом минимизирующих карт.
2. Для формулы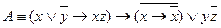 
составить множество Nf и изобразить его вершинами куба. Минимизировать методом Карно. Составить сокращенную ДНФ. Определить ядровые грани. Составить ДНФ Квайна.
3. Графически представлено нольмерное покрытие множества Nf . Составить СДНФ и СКНФ. Составить покрытие ядровыми гранями и записать соответствующую ДНФ Квайна. По данному рисунку составить карту Карно и минимизировать функцию. Сравнить результаты.
4. Дана функция f(00101110). Составить множество Nf и изобразить его графически.
5. Для функции из задания 4 составить СКНФ и сокращенную ДНФ. Изобразить сокращенную ДНФ. Найти ядровые грани и построить ДНФ Квайна.
6. Функция представлена картой Карно. Построить минимальную ДНФ с помощью этой карты.
 |
| ||
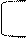
0 7. Дана функция от четырех переменных f(2,3,6,7,11,13,14,15)=1. Минимизировать ее методом Квайна и методом Карно. 1. Определение минимальной ДНФ. 2. Что собой представляет минимизирующая карта? 3. Сформулировать утверждение, которое используется в методе минимизирующих карт. 4. Алгоритм построения минимальной ДНФ с помощью минимизирующей карты. 5. Этапы минимизации СДНФ при применении метода Квайна. 6. Что представляет собой карта Карно? 7. Сколько ячеек можно включать в контуры и почему? 8. Что представляет собой единичный n-мерный куб? 9. Какие наборы входят в множество Nf ? 10. Что называется (n-r)- мерной гранью? Как определяется ранг конъюнкции и ранг ДНФ? 11. Задача минимизации в геометрической форме. 12. Какая грань называется максимальной? Что такое простая импликанта? Какая ДНФ называется сокращенной? 13. Методика построения сокращенной ДНФ. 14. Какое покрытие называется неприводимым? Какие ДНФ называются тупиковыми? Источник Тема 6 Минимизация булевых функций6.1 Сокращенная и тупиковая ДНФ 6.2 Метод импликантных матриц Цель данного раздела – изложение основных методов построения минимальных дизъюнктивно нормальных форм. 6.1 Сокращенная и тупиковая ДНФ. В разделе 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов. Дизъюнктивная нормальная форма называется Минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами. Заметим, что если некоторый символ в формуле, скажем Основной вопрос данного параграфа – это как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется Проблемой минимизации булевых функций. Существует тривиальный алгоритм построения минимальной ДНФ для произвольной булевой функции Число различных ДНФ, составленных из переменных Прежде чем доказать данное утверждение, приведем следующее определение. Конъюнкция Число R называется Рангом элементарной конъюнкции. В случае r=0 конъюнкция называется Пустой и Полагается равной 1. Так как каждая из N переменных Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций. Обозначим через Сопоставим каждой булевой функции
Соответствует подмножество Вершин трехмерного единичного куба
Данное соответствие является взаимно однозначным и обладает следующими свойствами: 1) булевой функции 2) булевой функции 3) булевой функции Докажем утверждение 2. Пусть Отсюда Тогда А это значит, что Отсюда Пусть Пусть Теперь ясно, что задача построения минимальной ДНФ сводится к отысканию такого покрытия подмножества Интервал Заметим, что соотношение Очевидно, что каждый интервал ДНФ Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно. Пример 1. Пусть Изобразим эти интервалы
Очевидно, что Данный геометрический подход дает и метод построения сокращенной ДНФ. Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме. Теорема 1. Если в произвольной ДНФ булевой функции F произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получиться сокращенная ДНФ функции F. Следовательно, чтобы найти сокращенную ДНФ, надо к произвольной ДНФ данной функции применить правило обобщенного склеивания Пример 2. Найти сокращенную ДНФ для функции Затем правило поглощения и находим сокращенную ДНФ: Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме. Теорема 2. Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции. Пример 3. Найти сокращенную ДНФ для функции
После раскрытия скобок с помощью дистрибутивного закона, получаем:
Так как
Далее, применяя правило поглощения, получаем сокращенную ДНФ:
Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты). Минимизирующие карты для булевых функций от трех и от четырех переменных изображены на следующих таблицах. Объединяя соседние клетки, соответствующие единичным значениям булевой функции f в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере. Пример 4. Найти сокращенную ДНФ для функции, заданной следующей таблицей. В данной таблице объединены клетки в максимальные интервалы
Этим интервалам соответствуют элементарные конъюнкции
Следовательно, сокращенная ДНФ для данной функции имеет вид:
Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ. Теорема 3. Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций. Доказательство этого утверждения следует из того факта, что покрытие подмножества Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают. Теорема 4. Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции. Пусть К – элементарная конъюнкция, входящая в сокращенную ДНФ. Предположим, что К содержит отрицание переменных. Обозначим через Получили противоречие с максимальностью интервала Пусть Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ
Элементарная конъюнкция Ввиду этого введем следующее определение. Покрытие области истинности булевой функции максимальными интервалами называется Неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции Теорема 5. Всякая минимальная ДНФ является тупиковой. Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым. Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже. Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций. 1. Выделяются все максимальные интервалы, и строится сокращенная ДНФ. 2. Строятся все тупиковые ДНФ. 3. Среди всех тупиковых ДНФ выделяются все минимальные ДНФ. Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем: 1) для булевой функции 2) для каждой вершины 3) составляем выражение вида 4) применяем к выражению вида (*) законы дистрибутивности и поглощения. В результате получаем Теперь каждая ДНФ Рассмотрим работу данного алгоритма на следующем примере. Пример 5. Рассмотрим булеву функцию, заданную следующей таблицей: Источник |
0
, встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
. Для этого все ДНФ, составленные из символов 
упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение 
. Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции 
, равно 
.
называется Элементарной, если 
при 
.
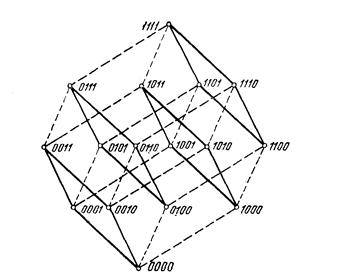
. Ясно, что число различных ДНФ, составленных из переменной 
множество всех точек 
, где 
. Ясно, что 
Из 
Соответствует подмножество 
;
соответствует подмножество 
;
соответствует подмножество 
.
.
.
.
.
ДНФ, где 
— элементарные конъюнкции. Подмножество 
называется интервалом R-го ранга, если оно соответствует элементарной конъюнкции К R-го ранга. Как показано выше, 
. Итак, с каждой ДНФ функции F связано покрытие 
, что 
.
— ранг интервала 
. Тогда 
совпадает с числом букв в ДНФ 
функции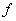 
.
, содержащий 
, такого, что 
.
выполняется тогда и только тогда, когда элементарная конъюнкция 
получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
— список всех максимальных интервалов подмножества 
.
булевой функции f, соответствующая покрытию подмножества 
. Обозначим 
, 
, 
. Найдем соответствующие этим конъюнкциям интервалы 
, 
, 
.
и 
— все максимальные интервалы. Интервал 
не является максимальным, ибо 
. Следовательно, покрытию подмножества 
соответствует сокращенная ДНФ функции 
, равная 
.
до тех пор, пока это возможно, а затем правило поглощения.
. Применяя правило обобщенного склеивания, получаем: 
.
.
.
, 
, то имеем:
.
.
.
, 
, 
, 
, 
произведение всех переменных, входящих в К без отрицания. Пусть 
– набор переменных, в которых всем переменным, входящим в 
. Очевидно, что при этих наборах значение функции 
.
— любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами 
. Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция 
обращалась в этой вершине в 1, то не содержала бы, во-первых, букв 
, и, во-вторых, букв 
. Поэтому в конъюнкцию 
, причем не все. Но тогда 
, которая покрывается только этим интервалом. Поэтому из покрытия 
поглощается дизъюнкцией остальных элементарных конъюнкций, т. е. 
.
из 
выделяем в сокращенной ДНФ функции F все такие элементарные конъюнкции 
, что 
;
(*)
.
является тупиковой ДНФ функции 
