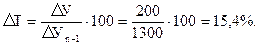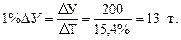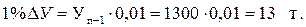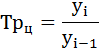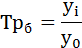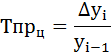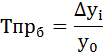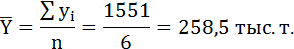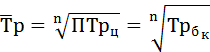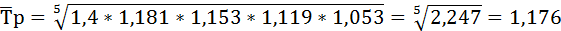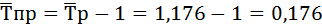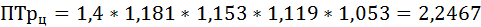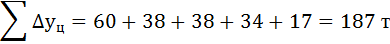Цепным способом абсолютное значение 1 прироста

Анализ динамики и структуры занятого населения

Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, который выражен в процентах и показывает значимость каждого процента прироста за тот же период времени, %:

(2.6)

Абсолютное значение одного процента прироста равно сотой части предыдущего уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

2006 = 0,01y2005 = 0,016157=61,51 тыс.чел.

2007 = 0,01y2006 = 0,016243=62,43 тыс.чел.

2008 = 0,01y2007 = 0,016397=63,97 тыс.чел.

2009 = 0,01y2008 = 0,016593=65,93 тыс.чел.

2010 = 0,01y2009 = 0,016368=63,68 тыс.чел.

2011 = 0,01y2010 = 0,016387=63,87 тыс.чел.

Среднегодовой абсолютный прирост (цепной) определим по формуле средней арифметической:

тыс.чел. (2.7)

Среднегодовой темп роста:

или 100,5%

Среднегодовой темп прироста:

=100,5%-100%=0,5%

Результаты расчетов представлены в таблице 2.3.

Таблица 2.3 Показатели динамики численности занятых в г.Москве за 2005-2011гг.

Источник

Абсолютное значение одного процента прироста

При анализе динамических рядов нередко ставится задача: выяснить, какими абсолютными значениями выражается 1 % прироста (снижения) уровней, так как в ряде случаев при снижении (замедлении) темпов роста абсолютный прирост может возрастать. В связи с этим возникает необходимость в расчете абсолютного значения одного процента прироста (снижения).

Абсолютное значение одного процента прироста представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах:

(9.16)

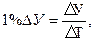
где 1 % ΔУ – абсолютное значение 1 % прироста; ΔУ – абсолютный прирост уровня; ΔТ – темп прироста, %.

После несложного преобразования формулы (10.16) получим, что

. (9.17)

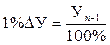
Это означает, что абсолютное значение 1 % прироста (снижения) равно 0,01 предыдущего уровня.

Например, известно, что объем выпуска яблочного сока в перерабатывающей организации за 2008 г. составил 1300 т, за 2010 г.–– 1500 т. Необходимо определить абсолютное значение 1 % прироста объема продукции в 2010 г. по отношению к 2008 г. Для расчета искомого показателя прежде всего найдем абсолютный прирост объема продукции в 2010 г. (1500-1300=200),а затем рассчитаем темп прироста продукции за этот же период:

Далее можно найти абсолютное значение 1 % прироста по выпуску яблочного сока:

К такому же результату приходим, рассчитав абсолютное значение 1 % прироста продукции более коротким путем:

Комплексное оформление результатов расчета основных показателей динамического ряда обычно проводится с помощью статистической таблицы. Например, при изучении пятилетней динамики урожайности озимого рапса в сельскохозяйственной организации «Днепр»были получены следующие результаты (табл. 9.6).

Т а б л и ц а 9.6. Основные показатели динамики урожайности озимого рапса

Годы	Урожайность, ц/га	Абсолютные приросты урожайности, ц/га	Темп роста, %	Темп прироста, %	Абсолютные значения 1 % прироста, ц/га
базисные	цепные	базисные	цепные	базисные	цепные
У	ΔУб	ΔУц	Тб	Тц	ΔТб	ΔТц	1 % ΔУ
—	—	0,0	—	—
-5	-5	85,7	85,7	-14,3	-14,3	0,35
-10	-5	71,4	83,3	-29,6	-16,7	0,35
-8	77,1	-22,9	8,0	0,35
-5	85,7	111,1	-14,3	11,1	0,35
В среднем:	29,4	-1,3	96,2	-3,8	0,35

Данные табл. 9.6 показывают, что для динамики урожайности озимого рапса в сельскохозяйственной организации за изучаемый период характерно снижение текущих уровней по сравнению с начальным (базисным) уровнем. Однако, начиная с серединного уровня, урожайность рапса постепенно повышалась, о чем свидетельствуют цепные темпы роста и прироста. Таким образом, для изучаемого динамического ряда характерна гиперболическая форма развития уровней.

Источник

Задача №56. Расчёт аналитических показателей динамики

Добыча нефти характеризуется следующими данными:

Годы	Добыча нефти, тыс. т
1-ый	150
2-ой	210
3-ий	248
4-ый	286
5-ый	320
6-ой	337

Произвести анализ ряда динамики по:

1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;

2) средний уровень и среднегодовой темп ряда динамики;

3) показать взаимосвязь между цепными и базисными показателями.

Решение:

Абсолютный прирост цепной (Δy_ц) – это разность между текущим уровнем ряда и предыдущим:

Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:

= 210 – 150 = 60 тыс. т.

В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:

Δy_{ц 3-й год} = 248 – 210 = 38 тыс. т.

Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.

Абсолютный прирост базисный (Δy_б) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:

Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.

Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:

Δy_б = 210 – 150 = 60 тыс. т

в 3-ем году базисный абсолютный прирост равен:

Δy_б = y₃ – y₂ = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).

Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:

(гр. 5 расчётной таблицы);

базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:

(гр. 4 расчётной таблицы).

Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:

Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:

Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:

или как разность между темпами роста и 100%, если темпы роста выражены в процентах:

Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).

Годы	Добыча нефти, тыс. т	Абсолютный прирост базисный, тыс. т	Абсолютный прирост цепной, тыс. т	Темп роста базисный, %	Темп роста цепной, %	Темп прироста базисный, %	Темп прироста цепной, %
А	1	2	3	4	5	6	7
1-ый	150	0	—	100,00	—	—	—
2-ой	210	60	60	140,00	140,0	40,00	40,0
3-ий	248	98	38	165,33	118,1	65,33	18,1
4-ый	286	136	38	190,67	115,3	90,67	15,3
5-ый	320	170	34	213,33	111,9	113,33	11,9
6-ой	337	187	17	224,67	105,3	124,67	5,3

Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.

2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:

Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической

где ПТр – произведение цепных темпов роста (в коэффициентах),

– конечный базисный темп роста (в коэффициентах),

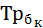
n – число темпов.

Среднегодовой темп прироста ряда динамики:

Добыча нефти ежегодно возрастала в среднем на 17,6%.

3) Между цепными и базисными темпами роста имеется взаимосвязь:

произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.

Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:

Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.

Источник