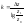27. Логарифмический метод
Логарифмический метод состоит в том, что с его помощью достигается логарифмически пропорциональное распределение неразложимого остатка по факторам. При его использовании не требуется установления очерёдности действия факторов (как в методе цепных подстановок). Однако данный метод имеет и недостатки, главным среди них является то, что он не универсален, так как не может быть применен при анализе любого вида моделей факторных систем. Логарифмический метод применяется при решении задачи прямого детерминированного факторного анализа только с мультипликативными факторными системами.
Математически данный метод описывается следующим образом. Факторную систему z = ab можно представить в виде lgz = lga + lgb,
Разделив обе части формулы на lg(z1 : z0) и умножив на Δz, получим :
Выражение (4.18) представляет собой для Δz не что иное, как его логарифмическое пропорциональное распределение по двум искомым факторам. Особенность логарифмического метода разложения состоит в том, что он позволяет определить безостаточное влияние не только двух, но и многих изолированных факторов на изменение результативного показателя, не требуя установления очерёдности действия.
Рассмотрим применение логарифмического метода, использовав данные табл. 4.8. Требуется определить влияние факторов первого порядка на изменение фондоотдачи основных средств предприятия. Факторная модель результативного показателя имеет вид:
Исходные данные для факторного анализа
Фондоотдача основных фондов, коэф. (ФО)
Удельный вес стоимости машин и оборудования в общей стоимости основных средств, коэф. (У)
Фондоотдача машин и оборудования,коэф. (ФОМ)
Фондоотдача основных средств предприятия уменьшилась на 0,046 пункта (0.9536423 – 1.0), в том числе за счет изменения:
удельного веса машин и оборудования в составе основных средств предприятия
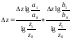
∆ФОУ = ∆ФО(lgIУ : lgIФО) = — 035 (lg 0.9933774 : lg 0.9536423) = -005;
фондоотдачи активной части основных средств:
∆ФОФОМ = ∆ФО(lgIФОМ : lgIФО) = — 035 (lg 0,96 : lg 0.9536423) = –0,3;
баланс отклонений: –0,35.
Таким образом, уменьшение фондоотдачи основных средств происходило за счет уменьшения значения двух факторов.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
2.2. Методика индексно-логарифмического анализа
Построение детерминированных факторных систем предусматривает моделирование факторов, воздействующих на результативный показатель. При этом моделирование факторной системы в экономическом анализе осуществляется посредством разделения факторов исходной модели.
Применение того или иного метода моделирования зависит от направления анализа, экономической сущности взаимосвязанных показателей-факторов.
Практика моделирования в экономическом анализе сложных моделей факторных систем, представленных в виде дроби (в частности, показатель фондоотдачи), использует метод расширения факторной системы, предусматривающий умножение числителя и знаменателя дроби на один и более вводимых показателей-факторов с последующим получением модели конечной факторной системы в виде произведения нового набора показателей- факторов (мультипликативная модель).
Среди методов оценки количественного влияния факторов при технико-экономическом анализе производственно-хозяйственной деятельности предприятий следует выделить: элиминирование, интегральный, дифференциального исчисления, логарифмический (индексно-логарифмический) и др.
В случае индексно-логарифмического метода за основу берется индекс исследуемого показателя, представляющего собой отношение среднегодового уровня фондоотдачи отчетного периода к базисному.
Индекс фондоотдачи (IF) рассчитывается:
, (2.1)
где F1 – фондоотдача отчетного периода;
F0 – фондоотдача базисного периода.
Влияние изменения какого-либо фактора, стоящего в числителе, на изменение результирующего показателя, используя логарифмический метод, можно представить:
, (2.2)
где 
— изменение фондоотдачи за счет xj-го фактора;
Для факторов, стоящих в знаменателе, влияние факторов на изменение фондоотдачи ( 
) определяется по формуле (2.2) с обратным знаком.
Общее изменение фондоотдачи (ΔF) за счет выделенных групп факторов определяется:
, (2.3)
где n – количество факторов, стоящих в числителе;
q – количество факторов, стоящих в знаменателе.
2.3. Особенности построения моделей фондоотдачи в бурении
Показатель фондоотдачи на практике исчисляют в стоимостном и натуральном измерении. Выбор метода его построения в бурении при экономической оценке степени использования ОПФ бурового предприятия зависит от конкретно поставленной перед исследованием задачи.
В общем виде, в бурении фондоотдача (F) в натуральном измерении определяется отношением годового объема проходки в метрах (Н) к среднегодовой стоимости основных фондов (СФ).
Используя метод взаимных индексов, показатель фондоотдачи, исчисленный в натуральном выражении, можно разложить на субиндексы, характеризующие в целом группу технико-технологических, организационных, структурных и ценностных факторов:
, (2.4)
где Н – проходка, м;
Тпр – производительное время бурения, ст.-мес.;
Тк – календарное время бурения, ст.-мес.;
п1 бу – среднегодовое количество буровых установок;
tк – календарное время бурения одной буровой установки, ст.-мес.;
СФ – среднегодовая стоимость ОПФ, тыс. руб.;
СФ а – среднегодовая стоимость активной части ОПФ, тыс. руб.;
СВО – среднегодовая стоимость ведущего бурового оборудования, тыс. руб.
Подставляя вместо соответствующих отношений их значения, получают:
, (2.5)
где VТ – техническая скорость бурения, м/ст.-мес.;
— удельный вес производительного времени в балансе времени бурения
скважин, доли ед.;
— календарное время бурения одной буровой установки, ст.-мес.;
— удельный вес ведущего бурового оборудования (рабочие машины и обо-
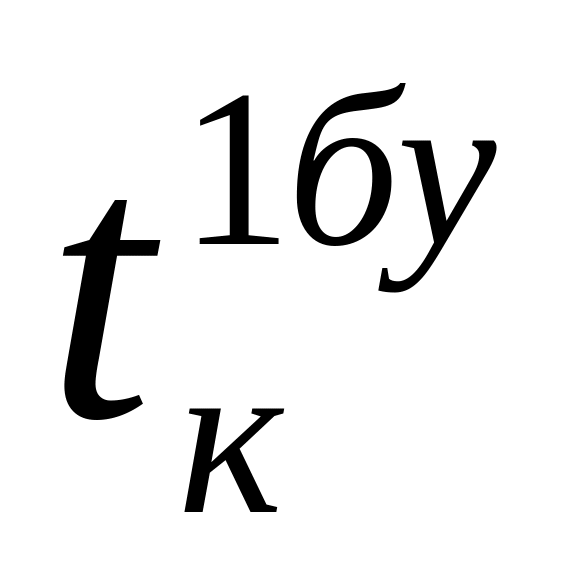
рудование) в стоимости активной части ОПФ, доли ед.;
— удельный вес активной части ОПФ, доли
— среднегодовая стоимость одной буровой установки, тыс. руб.
Динамика технической скорости бурения (VТ) наиболее полно характеризует технические и технологические возможности бурения скважин в конкретных геологических условиях. Изменение удельного веса производительного времени в календарном ( ) и календарное время бурения одной буровой установки ( ) характеризует организационно-экономические факторы — длительность производительной занятости буровых станков в бурении, прогрессивность методов организации производства, сокращение сроков ремонта, улучшение материально-технического снабжения, квалификацию кадров и др.
Изменение удельного веса стоимости буровых установок в активной части ОПФ ( ) и доля активной части в общей стоимости ОПФ характеризуют структурные сдвиги в ОПФ ( ).
Действие ценностного фактора характеризует изменение стоимости буровых установок ( ).
Индекс фондоотдачи (IF) за исследуемый период при разложении его на составляющие определяется произведением индексов показателей-измерителей рассмотренных выше факторов:
, (2.6)
Для определения влияния отдельных факторов на результирующий показатель производятся следующие вычисления:
, (2.7)
, (2.8)
, (2.9)
, (2.10)
, (2.11)
. (2.12)
Общее изменение фондоотдачи за счет выделенных факторов определяется следующим образом:
. (2.13)
Источник
Логарифмический метод
Обозначим индексами 1 и 0 данные, относящиеся к отчетному и базовому периодам соответственно.
В соответствии с рассматриваемой моделью можно записать:
Отметим, что логарифм здесь может быть любым — натуральным, десятичным или по любому другому основанию. Домножим обе части на ?z и разделим на lnz1z0. Получим:
Итак, прирост результативного показателя распределяется между факторами пропорционально логарифмам их изменения. Особенность метода в том, что при его использовании не требуется установления очередности действия факторов. Недостаток же заключается в том, что действует этот метод только для кратных и мультипликативных моделей. Пример 2.4 иллюстрирует использование логарифмического метода для анализа влияния факторов на изменение результативного показателя. Пример 2.4.
Анализ показывает, что направленность действий факторов противоположная, поэтому влияние каждого из них на изменение результативного фактора отчасти взаимно компенсируется. Задача 3 детерминированного факторного анализа представляет собой оценку влияния относительного изменения факторов на относительное изменение результативного показателя, т.е. определение отношения величины прироста, вызванного изменением любого фактора, к величине результативного показателя за базисный период в процентах. Она решается с помощью индексного метода и будет рассмотрена в разделе 2.7.4. Заканчивая раздел, отметим, что детерминистский подход достаточно распространен в анализе финансово-хозяйственной деятельности предприятий, поскольку позволяет выявить множество связей между факторами, влияющими на деятельность предприятия. Вместе с тем принципиальным недостатком детерминированного подхода является то, что он не позволяет разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели. Смысл данного утверждения совершенно очевиден. Дело в том, что любое предприятие работает в условиях действия множества факторов; объединить эти факторы в какую-либо модель, тем более жестко детерминированную, ни теоретически, ни практически не представляется возможным. Поэтому любое факторное разложение является весьма и весьма условным. Для примера приведем две модели, достаточно широко распространенные в факторном анализе:
где Т — товарооборот (выручка от реализации); Ч — численность работников; В — выработка на одного работника; Ф — фондоотдача; ОС — величина основных средств. Предположим, что проводится факторный анализ динамики изменения товарооборота с использованием этих двух моделей. Для этого необходимо построить следующие факторные разложения:
Из самой сути факторного анализа понятно, что общее приращение товарооборота в обеих моделях одно и то же, т.е.
Источник
