Центральная симметрия способ построения

Центральная симметрия — понятие, свойства и примеры фигур

Центральная симметрия – самая интересная и познавательная тема в геометрии, которую изучают в начальных классах школы и более тщательно — в 8 — 11 классах. Знания по этой теме обязательно пригодятся ученику в жизни.

Что такое центральная симметрия

Начнём с определения: центральная симметрия — одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В₁, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ_1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.

Центральную симметрию можно построить и в пространстве. В пространстве центральной симметрией называется словно зеркальное отображение какой-либо геометрической фигуры. Она представляет собой две одинаковые фигуры, соответственные точки которых попарно симметричны относительно точки пространства О.

Свойства центральной симметрии

Основные свойства следующие:

1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.

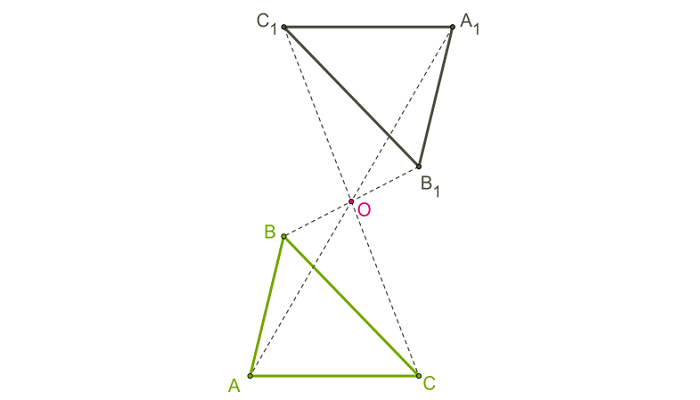
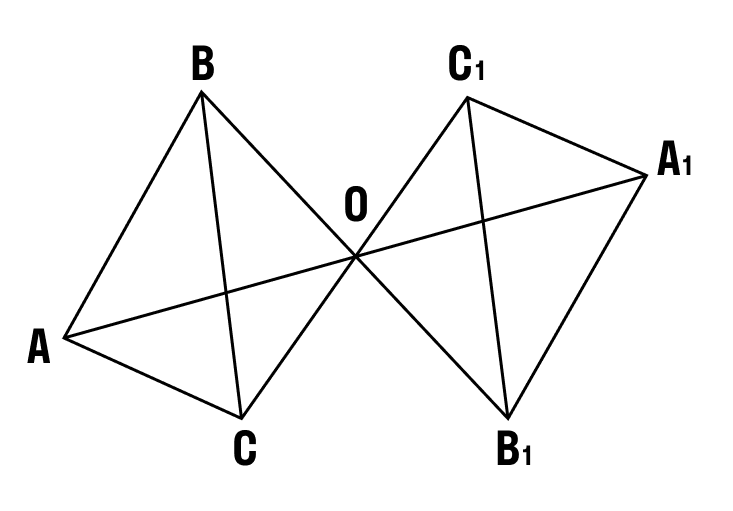
Посмотрим на рисунок. Треугольники АВС и А₁В₁С₁ симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А₁О, ВО=В₁О, СО=С₁О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;

2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;

3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;

4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А₁В₁ относительно точки О_.

Далее соединяем симметричные точки и получаем отрезки АА₁ и ВВ₁. Далее легко заметить, что отрезки АО и А₁О будут равны. Соответственно равны и отрезки ВО и В₁О. Углы, которые образуются при пересечении двумя прямыми точки О также равны.

Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А₁ и В,В_1. Значит они являются накрест лежащими при секущих АА₁ и ВВ₁. Задача решена, АВ и А₁В₁ параллельны;

5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.

Примеры фигур, обладающих центральной симметрией

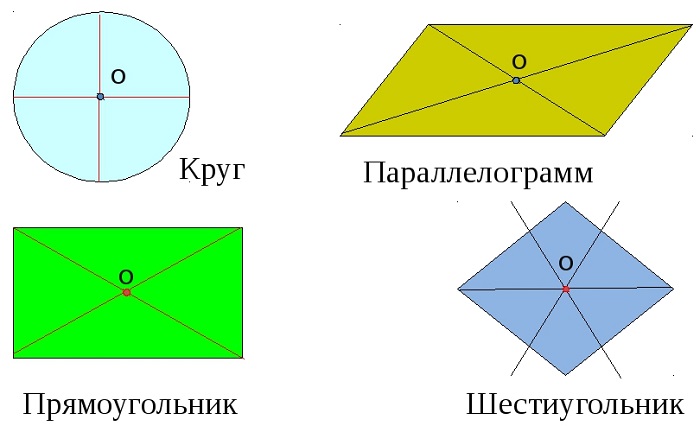
Фигур, как имеющих углы, так и без углов, но при этом обладающих центральной симметрией не так уж мало:

различные правильные многоугольники.

Интересные факты о центральной симметрии

Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией.

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке.

Ещё один очевидный пример – бабочка.

Великолепные узоры на её крылышках – четкая и яркая симметрия.

Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.

Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия.

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.

Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.

Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.

Источник

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равнобедренного треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник (если его сложить пополам) и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Измеряем расстояние от точки B до прямой l и от точки A до прямой l.
2. Проводим прямую от точки А через прямую l под прямым углом к прямой l, выводя за ось симметрии.
3. Проводим прямую от точки B через прямую l под прямым углом к прямой l, выводя за ось симметрии.
4. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

1. По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
2. Выводим прямые за точку О.
3. Измеряем отрезки AO, BO, CO и отмеряем такие же на противоположной стороне.
4. Получаем два центрально-симметричных треугольника.

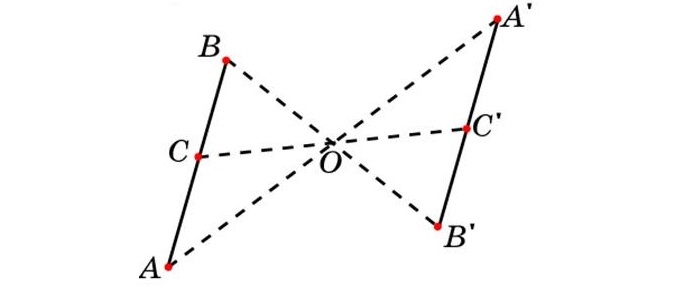
Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки равные отрезкам АО и OB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Геометрия. 8 класс

Конспект
Рассмотрим прямую a и точку, не принадлежащую ей.

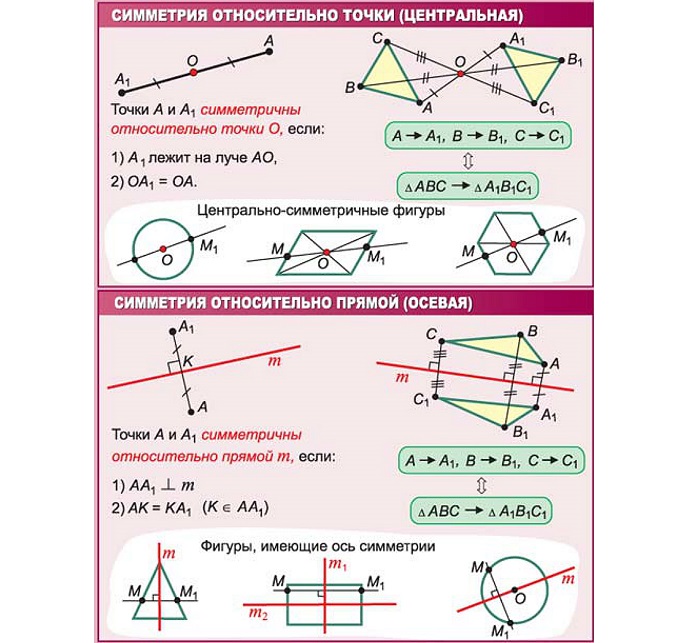
Точки А и А₁ называются симметричными относительно прямой а, если:
— эта прямая проходит через середину отрезка АА₁
— а ⊥ АА₁.
Прямая a называется осью симметрии. Если точка принадлежит прямой а, то она симметрична сама себе.
Составим алгоритм построения точки, симметричной данной.
Алгоритм построения
• Провести прямую b перпендикулярную прямой а
• Отложить от точки О на прямой b расстояние, равное ОА
• Получить точку А₁

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

(Цвет линий и букв черный)
Равносторонний треугольник имеет три оси симметрии. Неразвернутый угол имеет одну ось симметрии – прямую, содержащую биссектрису угла.

Подумайте, какие из данных фигур имеют ось симметрии и сколько?
Рассмотрим симметрию относительно точки.
Симметрия относительно точки
Две точки А и А₁ называются симметричными относительно точки О, если О – середина отрезка АА₁.

Составим алгоритм построения точки, симметричной данной относительно точки О.
Алгоритм построения
• Соединить точку А и точку О прямой и продолжить прямую за точку О
• От точки О отложить расстояние равное ОА
• Получить точку А₁

Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.

Центр симметрии имеет круг, квадрат.

Подумайте, какие из данных фигур имеют центр симметрии?

Слово «симметрия» греческое (συμμετρία), оно означает «соразмерность, пропорциональность, одинаковость в расположении частей», неизменность при каких-либо преобразованиях.
В словаре С.И. Ожегова симметрия – это соразмерность, пропорциональность частей чего-нибудь, расположенных по обе стороны от середины, центра.
С симметрией мы часто встречаемся в природе, архитектуре, искусстве, технике и быту. Симметрия в одежде – это символ строгости. Симметрия в архитектуре – это признак красоты и надежности. Некоторые люди утверждают, что симметрия – это совершенство.
Симметрией обладают некоторые буквы латинского и русского алфавита. Например, буква М обладает осевой симметрией, а буква Х – центральной симметрией.
Многие дорожные знаки обладают осевой или центральной симметрией. Гуляя по городу, приглядитесь к знакам. Найдите такие, которые имеют несколько осей симметрии и такие, которые не имеют осей симметрии.

Есть ось симметрии, центра симметрии нет Есть центр симметрии и 4 оси симметрии
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Источник