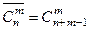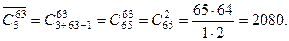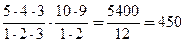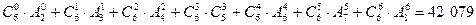Трое ребят собрали 40 яблок сколькими способами они могут их разделить

Раскладки

Раскладки. Задача 2. Сбор яблок. Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут их разделить, если все яблоки считаются одинаковыми?

Слайд 46 из презентации «Более сложные задачи по комбинаторике»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Более сложные задачи по комбинаторике.ppt» можно в zip-архиве размером 565 КБ.

Комбинаторика

«Принцип Дирихле» — Доказательство. Задачи. Средние линии треугольника. Область применения. Биография. Формулировка. Принцип Дирихле. Попарно не пересекающиеся отрезки. Принцип Дирихле для длин и площадей. 11 различных целых чисел.

«Элементы комбинаторики» — Понятие науки « Комбинаторика». Определение: Что такое перестановки? В чем состоит комбинаторное правило умножения? Что такое комбинаторика? Подбор комбинаторных задач. Отгадай ребусы. Число сочетаний из n элементов по k обозначают (читается: «С из n по k»). Сколько существует способов выбора учащихся для работы на пришкольном участке?

«Остовное дерево» — Как реализовать шаг. Условия оптимальности. Эквивалентность. Минимальное остовное дерево. Доказательство леммы. Оптимальное решение. Алгоритм Эдмондса. Алгоритм Прима находит решение. Эквивалентные задачи. Основная идея. Остовные деревья. Максимальный взвешенный ориентированный лес. Ориентированный лес.

«Теория графов» — Пользователи образовательных услуг (П). Информационные технологии (И). Ориентированные графы. Графовая модель образовательного учреждения. Преподаватели и сотрудники (работники) (Р). Древовидные графы. Задача выбора кратчайшего маршрута. Признаки уникурсальных графов: Лемма. Цепь — незамкнутый маршрут, состоящий из последовательности различных ребер.

«Виды графов» — Изображение вершин. Какая связь между графом и таблицей. Как называется взвешенный граф иерархической структуры. Файловая структура. Состав графа. Корень – главная вершина дерева. Графы. Дерево – граф иерархической структуры. Граф отношения «переписываются». Взвешенный граф. Иерархия. Самое главное.

«Комбинаторика 9 класс» — Комбинаторика – Москва Просвещение 1976г. Алгебра. Основное содержание: 1. Какую задачу называют комбинаторной. Для уборки территории требуется выделить 4 мальчика и 3 девочки. Решение: Решения I– варианта. События. Курьер должен развести пакеты в 7 различных учреждений. Вопрос 1 : Как обозначается произведение чисел от 1 до n?

Всего в теме «Комбинаторика» 25 презентаций

Источник

Сочетания с повторениями.

Дата добавления: 2015-07-23 ; просмотров: 1842 ; Нарушение авторских прав

П р и м е р . Трое ребят собрали 63 яблока. Сколькими способами они могут разделить их между собой?

Р е ш е н и е . Поставим в соответствие каждому делению яблок между ребятами сочетание с повторениями следующим образом. Будем считать, что множество А = 1, a₂, a₃> (ребята). Следует составить сочетания с повторениями длины m = 63, n = 3. Число способов разделить яблоки между ребятами равно

П р и м е р 1. Из порта А в порт В следуют 6 судов, а из порта В в порт С – три судна. Сколькими способами можно прибыть из порта А в порт С через порт В?

Из А в В – шестью способами , а из В в С – тремя способами. Всего 18 способов..

П р и м е р 2. На факультете 5 групп, участвующих в соревновании. Сколькими способами могут распределиться места в соревновании?

А₅ 3 = 5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 =120.

Сколькими способами могут распределиться первых три места? С₅ 3 = А₅ 3 / 3 ! = 20.

П р и м е р 3 .Пассажир забыл шифр. набранный в камере хранения – автомате, помнит только, что цифры его различны. Какое максимальное число попыток надо сделать, если шифр состоит из шести цифр, а на диске имеется 10 различных цифр?

А₁₀ 6 = 10 ∙ 9 ∙ 8 ∙ 7 ∙ 6 ∙ 5.

П р и м е р 4 .Имеется !5 деталей, из которых 5 нестандартных. Сколькими способами можно отобрать из этих деталей 5 так, чтобы 3 из них были нестандартными?.

С₅ 3 ∙ С₁₀ 2 =

Источник

Доказательство

Зашифуем каждую комбинацию с помощью нулей и единиц: для каждого типа напишем столько единиц, сколько предметов этого типа входит в комбинацию, а предметы различных типов отделить нулями. При этом число единиц будет k, а число нулей – n–1. Различным комбинациям будут соответствовать различные перестановки с повторениями из k элементов первого вида и n–1 элементов второго вида, а каждой перестановке с повторениями – своя комбинация. Итак, .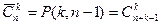

Встречаются задачи, в которых на сочетания с повторениями накладывается дополнительное условие, например, когда в комбинацию обязательно должны входить элементы r фиксированных типов, где r≤n. Эта задача легко сводится к уже решенной. Для того чтобы обеспечить присутствие заданных r типов, возьмем с самого начала по одному элементу каждого такого типа. Тем самым в k-сочетании окажутся заняты r мест. Поэтому ответом на задачу будет число 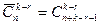. 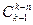В частности, если требуется, чтобы в каждом сочетании был элемент каждого из типов (n≤k), то получится .

Задача.

Сколько существует различных бросаний двух одинаковых кубиков?

Решение.

Переформулируем задачу. Всего при подбрасывании одного кубика возможны шесть ситуаций – имеем предметы шести различных типов. Подбрасывают два кубика, следовательно, из данных шести типов предметов необходимо выбрать два, причем нас не интересует порядок выбора, и допускается выбор одинаковых предметов. Таким образом, это задача на сочетания с повторением. По формуле для вычисления количества сочетаний с повторением имеем 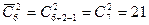различных бросаний двух одинаковых кубиков.

Многим комбинаторным задачам можно придать вид стандартной схемы. В этой схеме объекты (предметы) помещаются в ящики. Из-за наложения различных ограничений получаются различные задачи. Рассмотрим некоторые из них.

Имеется n₁ предметов одного сорта, n₂ – другого, . , n_k – k-го сорта. Сколькими способами можно разложить их в два ящика?

Так как в каждый ящик может попасть от 0 до n_i предметов i-го сорта (во второй все оставшиеся), по правилу произведения получаем (n₁+1)∙(n₂+1)∙. ∙(n_k+1) способов раскладки.

Двое ребят собрали 10 ромашек, 15 васильков и 14 незабудок. Сколькими способами они могут разделить эти цветы?

Необходимо 10 предметов одного вида, 15 – второго и 14 – третьего разложить в два ящика. Применяя рассуждения, аналогичные приведенным выше, получаем 11×16×15=2460 способов раздела цветов.

Следствие 1. Если все предметы различны (n₁=n₂=. =n_k=1), то их можно разложить 2 k способами.

Следствие 2. Если в каждый ящик нужно положить не менее s_i предметов i-го сорта, то получим формулу: (n₁-2s₁+1) × (n₂-2s₂+1) ×. × (n_k-2s_k+1).

Даны n различных предметов и k ящиков. Надо положить в первый ящик n₁ предметов, во второй – n₂, . в k-ый – n_k, где n₁+. +n_k=n. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике?

Выложим все предметы в один ряд. Это можно сделать n! способами. Первые n₁ предметов положим в первый ящик, вторые n₂ предмета – во второй ящик, …, k-ые n_k предметов – в к-ый ящик. Так как нас не интересует порядок предметов в ящике, то любая перестановка первых n₁ предметов не меняет результат раздела. Точно так же его не меняет любая перестановка вторых n₂ предметов, . k-ых n_k предметов. По правилу произведения получаем n₁! ×n₂!×. ×n_k! перестановок, не меняющих результата раздела. Таким образом, n! перестановок делятся на группы по n₁! ×n₂!×. ×n_k! перестановок в каждой группе, причем перестановки из одной группы приводят к одинаковому распределению предметов. Следовательно, число раздела предметов равно 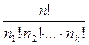=P(n₁. n_k).

При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?

Переформулируем задачу: необходимо разложить 28 предметов в 4 ящика по 7 предметов в каждый, причем порядок предметов в ящике не важен. Получаем 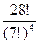способов распределения костей домино.

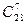
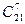
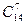
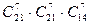
Можно было рассуждать другим способом. Первый игрок выбирает себе 7 костей из 28, это можно сделать способами. Второму необходимо выбрать 7 костей из оставшихся 21, это можно сделать способами. Третьему 7 из 14 – способов. А четвертый заберет оставшиеся. По правилу произведения получаем .

Даны n различных предметов и k одинаковых ящика. Надо положить в каждый ящик n₁ предметов, где n₁= 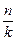. Сколькими способами можно сделать такое распределение, если не интересует порядок предметов в ящике, и все ящики одинаковы?

Задача отличается от предыдущей только тем, что ящики не пронумерованы. Так как k ящиков можно переставить k! способами, то полученный в предыдущей задаче результат необходимо разделить на k!. Всего 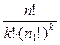способов распределения.

Сколькими различными способами можно разделить 8 книг на 4 бандероли по 2 книги в каждой?

Если бы интересовал порядок бандеролей, то существовало бы способов распределения книг. Так как не важно, в каком порядке будут отправлены бандероли, то полученное число необходимо поделить на 4!. Итого способов разделить 8 книг на 4 бандероли по 2 книги.

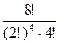
Сколькими способами можно разложить n одинаковых предметов в k ящиков?

Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных одинаковых предметов и k–1 разделяющих. Каждая такая перестановка определяет один из способов распределения. А именно предметы, расположенные до первого разделителя, положим в первый ящик, предметы, расположенные между первым и вторым разделителем, – во второй ящик и так далее, предметы расположенный после k–1 разделителя, – в k ящик. По формуле перестановок с повторениями число таких перестановок равно P(n, k-1)= 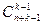. 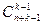Значит, всего имеем способов разложить n одинаковых предметов в k ящиков.

Трое ребят собрали с яблони 40 яблок. Сколькими способами они могут их разделить, если все яблоки считаются одинаковыми (то есть нас интересует, сколько яблок получит каждый, а не какие именно)?

Добавим два разделяющих предмета, тогда получаем Р(40, 2)=780 способа разделить яблоки.

Следствие 1. Если в каждый ящик надо положить не менее r предметов, то получим: P(n-k×r,k-1) способов.

Следствие 2. Если в каждый ящик надо положить хотя бы один предмет, то r=1 и получим P(n-k,k-1)= 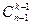способов распределения.

Сколько существует способов разложить n различных предметов в k ящиков, если нет никаких ограничений?

Каждый предмет можно положить в любой из k ящиков. Получаем k n способов распределения предметов по ящикам.

Сколькими способами можно разделить 8 различных пирожных между 5 детьми?

Необходимо разложить 8 предметов по 5 ящикам. Это можно сделать 5 8 =390 625 способами.

Сколькими способами можно поместить n различных предметов в k ящиков, если не должно быть пустых ящиков?

Данные r ящиков остаются пустыми, если в k–r ящиков предметы кладутся без ограничений. r пустых ящиков можно выбрать C_n k способами. В оставшиеся k–r ящиков предметы можно разложить (k–r) n способами. По формуле включений и исключений число распределений, при которых хотя бы один ящик остается пустым, равно 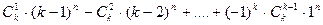. Тогда количество распределений, при которых ни один ящик не окажется пустым, равно

k n -( ).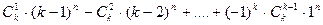

Сколькими способами можно послать по почте 8 различных фотографий, использовав 5 конвертов?

Переформулируем задачу: необходимо 8 предметов разложить в 5 ящиков. Посылать пустые конверты не рационально, поэтому накладывается запрет на пустые ящики.

Применяя полученную выше формулу, получаем

5 8 — ×4 8 + ×3 8 — ×2 8 + ×1 8 =126 020.

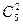
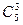
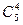
Имеется n₁ предметов одного сорта, n₂ – другого, . , n_s – s-го сорта. Сколькими способами их можно разложить по k ящикам, если не должно быть пустых ящиков?

Применяя рассуждения, аналогичные предыдущей задаче, получим следующую формулу

.

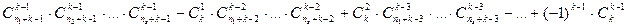
Сколькими способами можно разделить 8 яблок, 10 груш и 7 апельсинов между 4 детьми, если каждый должен получить хотя бы один фрукт?

Требуется 8 предметов одного сорта, 10 второго и 7 третьего разложить в 4 ящика так, чтобы ни один ящик не оказался пустым. По предыдущей формуле получаем

способов такого распределения.

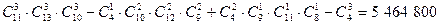
Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем все n предметов должны быть использованы?

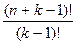
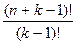
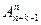
Добавим к n предметам k–1 одинаковых разделяющих предмета. Рассмотрим все возможные перестановки из n различных предметов и k–1 одинаковых. Каждая такая перестановка определяет один из способов распределения. Всего таких перестановок . Значит, n различных предметов можно разложить в k ящиков, с учетом расположения их в ящиках, = способами.

К тому же результату можно было прийти и другим путем. Переставим всеми возможными способами данные n предметов (n! способов). Теперь считаем предметы неразличимыми, их можно разложить в k ящиков Р(n, k–1) способами. Получаем n!∙Р(n,k–1)= 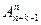способов распределения этих вещей по к различным ящикам с учетом порядка их расположения в ящиках.

Имеются 6 различных сигнальных флагов и 3 мачты, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке вывешены флаги. Сколькими способами можно развесить флаги, если все флаги должны быть использованы, но некоторые из мачт могут оказаться пустыми?

Имеем 6 предметов, которые необходимо разложить в 3 ящика, причем порядок предметов в ящике важен. Это можно сделать 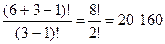способами.

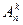
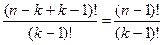
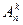
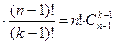
Следствие. Если не должно быть пустых ящиков, то выберем k предметов и разложим по одному в каждый ящик. Это можно сделать способами. Оставшиеся n–k предметов разложим в k–1 ящик, причем теперь некоторые ящики могут оказаться пустыми. Это распределение можно осуществить способами. Всего имеем способов распределения.

Сколькими способами можно распределить n различных предметов по k различным ящикам с учетом порядка расположения предметов в ящиках, причем не все n предметов могут быть использованы и некоторые ящики могут оказаться пустыми?

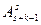
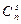
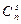
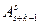
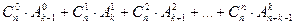
Разобьем все возможные комбинации на классы. В s класс войдут комбинации, в которых использованы ровно s предметов. Из предыдущей задачи известно, что s предметов можно разложить по k ящикам способами. s предметов из данных n можно выбрать способами. Всего в s класс войдут × комбинаций. По правилу суммы имеем

способов распределения n различных предметов по k различным ящикам с учетом порядка их расположения в ящиках, если не все n предметов могут быть использованы.

Имеются 6 различных сигнальных флагов и 3 мачты, на которые их вывешивают. Значение сигнала зависит от того, в каком порядке вывешены флаги. Сколькими способами можно развесить флаги, если не все флаги могут быть использованы и некоторые из мачт могут оказаться пустыми?

Имеем 6 различных предметов, которые необходимо разложить в 3 ящика, причем порядок предметов в ящике важен и не все ящики и предметы могут быть использованы. По формуле получаем

Следствие. Если не должно быть пустых ящиков, то в этом случае имеем

способов распределения.

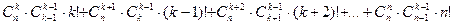
Частотой появления события в серии испытанийназывается отношение числа наступления этого события в данной последовательности испытаний к общему числу испытаний.

Вероятностью случайного события называется отношение числа равновозможных элементарных событий, благоприятствующих этому событию, к числу всех равновозможных элементарных событий.

Равновозможными элементарными событиями будем считать такие события, любое из которых по отношению к другим событиям не обладает никаким преимуществом появляться чаще другого при многократных испытаниях, проводимых в одинаковых условиях.

Например, при бросании игральной кости возможны шесть различных результатов; из них лишь в одном случае выпадает шестёрка. Поэтому вероятность выпадения шестёрки равна 1/6.

Задача.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник