Метод триангуляции
Триангуляция – метод для измерения расстояний, часто с использованием лазера. Он использует способность лазерного луча распространяться в хорошо коллимированной форме (т.е. с малой расходимостью) на большие расстояния. Обычно лазерный луч освещает точку, расстояние до которой от лазерного устройства необходимо измерить; по существу, лазер используется в качестве указателя. Рассеянное или зеркальное отражения от этой точки контролируются детектором, который устанавливается на некотором расстоянии от лазерного луча, таком, что источник лазерного излучения, объекта и детектор образуют треугольник. На детекторе линза фокусирует отраженный свет на ПЗС-матрице, и положение яркого пятна на чипе показывает направление входящего света, т. е. угол между лазерным лучом и возвращенным светом, откуда расстояние и может быть рассчитано.
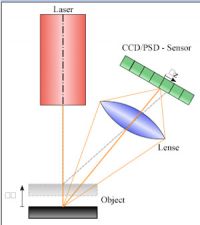
Высокая скорость обнаружения позволяет отслеживать положение движущейся или вибрирующей части, например, какой-либо машины. Полученная точность может, как правило, достигать одной тысячной доли расстояния. Для рассеянного отражения расстояние может быть ограничено требованием получить определённую отраженную оптическую мощность; при зеркальном отражении могут быть измерены гораздо большие расстояния, но требуется какое-либо угловое выравнивание в направлении измерения.
Принцип триангуляции также может быть реализован с помощью лазерного луча, в направлении которого производится быстрое сканирование в двух измерениях. Таким образом, можно получить трехмерные (3D) изображения.
Требования к лазерному источнику:
В идеале, лазерный источник для триангуляции должен иметь высокое качество пучка, чтобы осветить небольшое пятно на большом расстоянии. Так же требуется определенная оптическая мощность, особенно для целей с рассеянным отражением. Лучше использовать безопасные для глаз длины волны лазерного излучения (например, в 1.5 мкм области), хотя видимый луч помогает убедиться, что подсвечена правильная точка.
Источник
Триангуляция — построение, метод и сущность
Известно, что триангуляция как геодезический термин означает способ создания геодезических сетей. Да, это так. Но следует начать с другого.
Изначально с возникновением потребности человека в познании, обычное мышление приводит его к накоплению определенного багажа знаний. С развитием научного мышления все эти знания систематизируются, в том числе разъясняются на основе фактов, явлений и доказательств. Применяя теоретические предположения на практике, возникают своего рода критерии истины. То есть имеют ли подтверждения практическим путем все те предположения, которые с помощью определенных способов дают конкретный результат. Пожалуй, одним из таких научных методов, решающих задачу по высокоточному измерению больших расстояний между пунктами на земной поверхности с построением примыкающих друг к другу треугольников и измерений внутри них стал способ триангуляции.
Первым кто изобрел и применил метод триангуляции (1614-1616), был великий голландский ученый Виллеброрд Снелл (Снеллиус). В те годы уже были предположения о том, что Земля является планетой в космическом пространстве и имеет форму сферы (из космологии Джордано Бруно 1548-1600). Установление точных размеров планеты имело большое практическое значение по ее освоению в дальнейшем. Вот для этого в Нидерландах через постройку ряда треугольников были впервые выполнены градусные измерения дуги меридиана способом триангуляции. Что имеется ввиду. Выполнив измерения между жесткими геодезическими пунктами с разностью широт между ними в один градус (у Снеллиуса 1º11´30″) способом триангуляции и получив конкретное расстояние дуги, голландский математик обычным расчетом мог получить длину всей окружности меридиана. Очевидно, что вычислить радиус Земли, приняв ее фигуру за форму шара (эллипса), оставалось делом техники.
В завершение исторического экскурса можно выделить взаимосвязанность и выборность научных познаний для будущего практического применения человеком. И не удивительно, что изобретение способа триангуляции произошло именно в Нидерландах, которые на тот момент считались ведущей морской державой с потребностью новых познаний в навигации, географии, астрономии и конечно геодезии.
Сущность метода
Триангуляция заключается в определении пространственного местоположения специально закрепленных на местности геодезических пунктов в вершинах целого ряда треугольников. Изначально, с высокой степенью точности (до долей секунд) определяют азимуты исходных направлений ab, ba, mn, nm (рис.1.Триангуляционный ряд треугольников по меридиану). Следующим этапом будет определение астрономических координат (широты и долготы) в пунктах измерений азимутов двух исходных базисов. В каждой паре жестких сторон (ab, mn) координаты измеряются только в одной точке, например a, m (рис.1). При этом следует обратить особое внимание на определение астрономических широт в ряду треугольников, расположенных по направлению меридианов. При измерениях в треугольниках, сформированных вдоль параллелей, необходимо уделить должное внимание определению астрономических долгот. Далее производят измерения длин двух базисных сторон (ab, mn). Эти стороны имеют сравнительно не большие длины (порядка 8-10 км). Поэтому их измерения более экономичные и точные относительно сторон cd, tq, составляющих расстояния от 30 до 40 км. В следующую очередь выполняется переход от базисов ab, mn через угловые измерения в ромбах abcd и mntq к сторонам cd, tq. А затем последовательно практически в каждой вершине треугольников cde, def, efg и других измеряются горизонтальные углы до примыкания к следующей основной стороне tq всего ряда треугольников. Через измеренные углы треугольника с измеренной базисной или вычисленной основной стороной последовательно вычисляются все другие стороны, их азимуты и координаты вершин треугольников.
Рис.1. Триангуляционный ряд треугольников по меридиану.
Триангуляционные сети
После первого применения градусного измерения дуги Снеллиусом триангуляционный метод становится основным способом в геодезических высокоточных измерениях. С XIX века, когда триангуляционные работы стали более совершенными с его помощью стали формироваться целые геодезические сети, строящиеся вдоль параллелей и меридианов. Самая знаменитая из всех известна под наименованием геодезической меридианной дуги Струве и Теннера (1816-1852) в последствие зачислена в мировое наследие по ЮНЕСКО. Ее триангуляционный ряд протянулся по Норвегии, Швеции, Финляндии и России от Северного Ледовитого океана до Черного моря в устье Дуная и составил дугу в 25º20´(рис.2).
За основу геодезических сетей триангуляции в нашей стране принята схема профессора Ф.Н.Красовского (рис.3). Ее суть заключается в применении принципа построений от общего к частному. Изначально закладываются вдоль меридианов и параллелей пункты, образующие ряды треугольников протяженностью в пределах 200-240 км. Длины сторон в самих треугольниках составляют 25-40км. Все астрономические измерения азимутов, координат (широт и долгот) выходных точек на пунктах Лапласа (1) и промежуточных астрономических точках (2), высокоточные базисные (3) геодезические измерения и в каждой точке этой цепи должно соответствовать установленным требованиям I класса точности (рис.3). Замкнутый полигон из четырех триангуляционных рядов представляет собой фигуру, напоминающую квадрат с периметром равным ориентировочно около 800 км. Через центральные части первоклассных рядов триангуляции устраиваются в направлении друг к другу основные ряды триангуляционной сети II класса (рис.3) соответствующей точности. Базисные длины сторон в этих рядах не измеряются, а принимаются базисы со сторон триангуляции I класса. Аналогично отсутствуют и астрономические пункты. Возникшие четыре пространства заполняются сплошными триангуляционными сетями и II, и III классов.
Рис.3.Государственные сети триангуляции.
Безусловно описанная схема развития сетей триангуляции по Красовскому не может закрыть всю территорию страны ввиду понятных причин больших лесных и не заселенных территорий страны. Поэтому с запада на восток вдоль параллелей были проложены отдельные ряды первоклассной триангуляции и полигонометрии, а не сплошная триангуляционная сеть.
Достоинства триангуляции
В развитии геодезической науки и ее практического применения очевидны достоинства триангуляционного способа измерений. С помощью этого универсального метода возможно:
- определение положения геодезических точек на значительно удаленных расстояниях;
- выполнение основных работ по строительству геодезических сетей на всей территории страны;
- обеспечение основой всех топографических съемок;
- выстраивание через основные геодезические работы различных систем координат;
- производство инженерных и изыскательских работ;
- периодическое определение размеров Земли;
- изучение перемещений земной поверхности.
Источник
Результаты моделирования триангуляционного способа определения дальности с применением двух и трёх станций
конструкторское бюро автоматики»
644027, г. Омск, Космический пр. 24а
E-mail: ckba @ omsknet. ru
Результаты моделирования триангуляционного способа определения дальности с применением двух и трёх станций
Целью данной работы является оценка точности определения координат наблюдаемого объекта (цели) в пространстве триангуляционным способом [1]. В качестве субъектов наблюдения (наблюдателей) взяты пассивные радиолокационные станции, что соответственно подразумевает под объектом слежения активный источник радиосигнала.
1 Описание модели
«Слабым местом» пассивных РЛС является проблема определения дальности до источника радиосигнала (цели), поэтому в данной работе в качестве основного критерия точности определения координат объекта была принята погрешность определения дальности от некой опорной станции до цели, а точнее рассматривались границы дальностей – минимальное и максимальное значение в каждом случае.
Моделирование выполнялось при следующих исходных данных:
— были рассмотрены случаи определения координат (дальности) объекта триангуляционным способом двумя и тремя станциями, координаты положений которых априорно известны;
— каждая станция обладает возможностями двумерного пеленгования цели (определения азимута, угла места);
— точность (среднеквадратичная ошибка) пеленгования объекта станциями принималась в диапазоне 1-3°, распределённой по нормальному закону, одинаковой в обеих плоскостях пеленгования;
— проблема идентификации цели станциями (однозначного её определения) в данной работе не рассматривалась, т. е. цель была всегда одна;
— границы определяемых дальностей до цели определялись по порогу 90% вероятности попадания цели в область минимальных значений суммарных среднеквадратичных пеленгационных ошибок всех станций
,
где 
– количество используемых субъектов слежения (станций); 
– среднеквадратичные значения пеленгационных ошибок в азимутальной плоскости; 
– среднеквадратичные значения пеленгационных ошибок в угломестной плоскости; 
– искомый порог.
Пороговое значение находилось эмпирическим путём – по смоделированной выборке 104 значений и каждой станции. Далее в программе модели искались точки максимальных и минимальных значений дальностей, суммарная разность пеленгационных углов между которыми и истинным положением цели удовлетворяла условию
, где 
.
Несмотря на то, что неравенство Колмогорова [2] даёт описание аналитического выражения по нахождению значения , а точнее его максимального граничного значения, различие , полученных эмпирическим и аналитическим путём, отличались в разы. Во всех случаях эмпирические значения получились меньше аналогичных предельных границ значений неравенства Колмогорова, что в принципе не противоречит существующим выкладкам теории вероятностей.
Построение рабочей модели и моделирование проводилось в среде пакета прикладных программ MATLAB. Следует отметить, что модель была полностью реализована под проведение расчётов с учётом трёхмерных координат пространства. Модель поддерживает возможность указания трёхмерных координат не только объекту, но и любому субъекту слежения. Помимо широкого применения трёхмерной прямоугольной декартовой системы координат в модели применяется и сферическая.
В декартовой системе координат используются относительные единицы длин. При моделировании было выдержано вынужденное ограничение: поиск (расчёт) максимальной дальности положения цели принудительно прерывался при превышении двукратного истинного значения. Существует несколько причин введения такого ограничения:
— определённые комбинации положений объекта и субъектов не позволяют провести определение координат объекта триангуляционным способом, соответственно максимальная граница дальности расстояния до объекта в данном случае просто не определена;
— поиск (расчёт) значения максимальной дальности в модели проводился итерационным способом, соответственно поиск больших значений дальности требует выполнения большого количества машинных математических операций, что, в свою очередь, значительно увеличивает общее время проведения расчётов;
— большие значения ошибок определения дальностей уже не представляют практического интереса, следовательно, нет смысла их находить.
Поэтому следует помнить, что все представленные далее в работе результаты моделирования содержат в себе вышеописанное ограничение. Учитывая итерационный алгоритм модели поиска значений дальностей, с присущей ему дискретностью поиска значений, точность поиска ошибки определения дальностей была установлена не грубее 0,1% истинного значения дальности до цели.
На рис. 1 представлена дополнительная информация, необходимая для пояснения дальнейших приводимых в работе результатов. Станция 1 всегда является опорной, т. е. относительно её определяются дальности до цели. Также с целью упрощения представления результатов в дальнейшем примем истинное расстояние от опорной станции до цели всегда равным 1.
Рис. 1 Расположения двух (слева) и трёх (справа) станций на поверхности «земли»
На рис. 2‑4 представлены результаты совместной работы двух станций по определению координат (дальности) цели триангуляционным способом, на рис. 4‑8 – трёх станций. На представленных рисунках приняты следующие сокращения: α – истинный азимут цели относительно опорной станции; β – истинный угол места цели относительно опорной станции; γ – угол, характеризующий положения станций (см. рис. 1); σ – среднеквадратичное значение пеленга цели станциями; Rист ≡ 1 – истинное расстояние до цели; d/Rист – размер базы (см. рис. 1), выраженный в единицах расстояния до цели; Rmin – ближняя граница определения дальности до цели; Rmax – дальняя граница определения дальности до цели (Rmin
Источник
