Три способы описания алгоритма

Алгоритмизация. Понятие алгоритма. Свойства и способы описания алгоритмов.

Вы будете перенаправлены на Автор24

Решение задач с использованием компьютера основано на понятии алгоритма, который является точным описанием вычислительного процесса, ведущего от варьируемых начальных данных к конечному результату.

Алгоритмы заложены в основе каждой программы, а также они встречаются во многих сферах деятельности человека (например, рецепты, схема вязания или танца).

Алгоритмизация является техникой разработки алгоритма для решения задач на ЭВМ.

Понятие алгоритма

Алгоритм представляет собой точное описание определенного процесса, инструкцию по его выполнению.

Процесс разработки алгоритма — достаточно сложный и трудоемкий.

Можно также сказать, что алгоритм представляет собой конечную последовательность команд для исполнителя, направленную на достижение конкретной цели.

Цель же, в свою очередь, является достижением желаемого результата.

В качестве исполнителя могут выступать люди, живые существа, автоматические устройства, способные к исполнению и восприятию команд.

Перечень команд, воспринимаемых и выполняемых (по возможности) исполнителем, называют системой команд.

Каждый алгоритм предназначен для конкретного исполнителя. Исполнение алгоритма начинается с первой команды. После того, как ее исполнили, переходят к следующей команде и так до конца алгоритма.

В качестве примера алгоритма можно вспомнить известный всем со школы арифметический способ сложения двух положительных чисел «столбиком». Алгоритм данной задачи представим в виде системы следующих действий:

• выделим в слагаемых разряды единиц и сложим единицы;
• при получении суммы меньшей 10 запишем ее в разряде единиц под нижним числом;
• при получении суммы большей или равной 10 запишем в разряде единиц только количество единиц, затем выделим в слагаемых разряд десятков и запишем полученный при сложении единиц десяток над разрядом десятков первого (верхнего) слагаемого;
• сложим десятки и т. д.

Готовые работы на аналогичную тему

Аналогичные указания дают для сложения единиц других разрядов числа. Системой-исполнителем этого алгоритма может стать как ЭВМ, так и человек.

Понятие алгоритма в теорию и практику обучения вошло в конце $50$-х годов прошлого столетия в связи с развитием программированного обучения и применением обучающимися машин.

Способы описания алгоритмов

Существуют различные способы описания алгоритмов. Приведем основные из них:

• словесный (пошаговое описание);
• табличный и в виде формул;
• графический (в виде схем);
• с использованием псевдокода (алгоритмического языка).

Алгоритмический язык является формальным языком, предназначенным для записи алгоритма. В его состав входят набор основных символов (алфавит), система точных правил построения текстов (синтаксис) и система соответствия синтаксически допустимых текстов языка описываемым действиям и объектам (семантика).

Множество языков программирования, используемых при ре¬шении задач на ЭВМ, являются алгоритмическими.

Псевдокод представляет собой способ описания логики программы до начала ее программирования и занимает промежуточное положение между машинным языками и естественными.

Под схемой алгоритма понимают графическое пред¬ставление последовательности шагов алгоритма, наглядно показывающее взаимосвязь опера¬ций, которые осуществляются в алгоритме на каждом шаге, и их очередность. Другими словами, для графического изображения структуры алгоритма используется блок-схема.

В соответствии с блок-схемой последовательность действий указывается с по¬мощью стрелок, которые соединяют отдельные блоки и показывают, какой блок и за каким должен быть выполнен.

Свойства алгоритмов

Существует ряд определенных требований к алгоритмам. Перечислим семь важных свойств, которыми должен обладать каждый алгоритм:

1. Наличие ввода исходных данных.
2. Наличие вывода результата выполнения.
3. Однозначность, так как компьютеру понятны лишь однозначные инструкции.
4. Общность, в соответствии с которой алгоритм может использоваться не только для решения одной задачи, но и целого класса задач.
5. Корректность, согласно которой при выполнении алгоритма должно быть всегда правильное решение задачи.
6. Конечность означает, что решение задачи необходимо получить за конечное число шагов.
7. Эффективность означает, что для решения задачи необходимо использовать ограниченные ресурсы компьютера (объем оперативной памяти, процессорное время и т. д.).

Эффективность алгоритма определяют с учетом потребляемых ресурсов компьютера, к которым относят быстродействие (количество выполняемых операций и затраты трудоемкости на каждую из них) и общий объем оперативной памяти, которая выделяется под данные. Приведенные показатели могут иногда быть противоречивыми: так в результате повышения быстродействия могут потребоваться дополнительные расходы памяти и наоборот. При возможности улучшения одного показателя без ущерба для другого необходимо этого добиваться. В случаях, когда возникает дилемма, рекомендуется предпочесть экономию памяти в ущерб производительности, поскольку тактовая частота процессоров растет опережающими темпами по сравнению с объемами оперативной памяти.

Специалистами предлагается ряд мер для повышения эффективности.

Блок-схемы

Основные алгоритмические структуры изображаются с помощью специальных графических символов. Все составляющие блок-схемы соединяются между собой в той последовательности, в какой они должны быть исполнены.

Кроме того, в алгоритмах используются разветвляющие и циклические блоки.

Обязательными блоками являются блоки начала и конца алгоритма. Между ними размещаются остальные блоки алгоритма.

Операторный блок (блок действия) содержит команды обработки данных.

Блок проверки условия предполагает 2 варианта дальнейшего развития решения задачи, в зависимости от того или иного выполнения поставленного условия.

Блоки ввода или вывода данных. Для выполнения алгоритма необходимы не только команды, но и данные, поступающие из вне. Для получения этих данных используется блок ввода. Для того, чтобы можно было вывести результат выполнения программы, либо какое-нибудь сообщение используют блок вывода.

Ниже на рисунке представлены графические изображения основных блоков алгоритма.

Источник

Способы описания алгоритмов

Существуют несколько способов описания алгоритма: словесное, псевдокод, блок-схема, программа.

Словесное описание представляет структуру алгоритма на естественном языке. Запись алгоритма осуществляется в произвольной форме, никаких правил не существует.

Псевдокод – описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.

Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слов и конструкций.

Блок-схема – описание структуры алгоритма с помощью геометрических фигур с линиями – связями, показывающими порядок выполнения отдельных инструкций. В блок – схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.

Основные конструкции, использующиеся для построения блок – схем.

— процесс, предназначенный для описания отдельных

действий

ввод/вывод с неопределенного носителя

Нет Да — проверка условия

— — предопределенный процесс, предназначенный для

— обращения к подпрограмме.

Лекция 5.2. Блок-схемы алгоритма

Алгоритмы решения задач

Логическая структура алгоритма решения любой задачи может быть выражена комбинацией трех базовых структур: следования, ветвления и цикла (это содержание теоремы Бема – Якопини).

Линейная структура (следование) самая важная из структур. Она означает, что действия могут быть выполнены друг за другом (рис. 5.2.1.).

Выполнить B

Выполнить А

Прямоугольники могут представлять как одну единственную команду, так и множество операторов, необходимых для выполнения сложной обработки данных.

Опишем алгоритм сложения двух чисел на псевдокоде и в виде блок-схемы (рис. 5.2.2.).

2. Ввод двух чисел a, b

3. Вычисляем сумму S = a + b

4. Вывод S

S= a + b

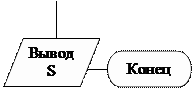Рис. 5.2.2. Блок — схема к примеру 5.2.1.

Ветвление (развилка) – это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка условия, а затем выбирается один из путей (рис. 5.2.3). Если условие имеет значение «Истина», то выполняется «Действие А». Если условие имеет значение «Ложь», выполняется «Действие В». Эта структура называется, также «Если – ТО – ИНАЧЕ» или «развилка». Каждый путь (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран. Может оказаться, что для одного из результатов проверки ничего выполнять не надо. В этом случае можно применить только один обрабатывающий блок (рис. 5.2.4).

Вход

Ложь (НЕТ) Истина (ДА)

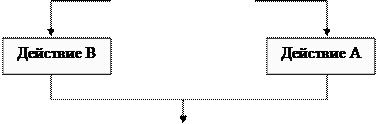Рис. 5.2.3. Полное ветвление

ДА НЕТ

Действие А

Рис. 5.2.4. Структура «непол-

ное ветвление»

Такая структура называется «неполным ветвлением» или «неполной развилкой».

Вывести значение наибольшего числа из двух чисел (рис. 5.2.5).

Псевдокод:

1. Ввод двух чисел a, b

2. ЕСЛИ ab, ТО «выводим a»,

ИНАЧЕ «выводим b»

3.

Конец.

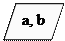
Рис. 5.2.5. Блок – схема к примеру 5.2.2.

Цикл (или повторение) предусматривает повторное выполнение некоторого набора команд алгоритма. Циклы позволяют записать длинные последовательности операций обработки данных с помощью небольшого числа повторяющихся команд. Различают два типа циклов: «цикл с предусловием» и «цикл с постусловием».

Цикл с предусловием («Пока») (рис. 5.2.6).

Тело цикла

Ложь

Рис. 5.2.6. Структура цикла «Пока».

Цикл начинается с проверки логического выражения. Если оно истинно, то выполняется тело цикла, затем все повторяется, пока логическое выражение сохраняет значение «истина». Как только оно становится ложным, выполнение операций прекращается и управление передается дальше. Особенностью цикла с предусловием является то, что если изначально логическое выражение имеет значение «ложь», то тело цикла не выполнится ни разу.

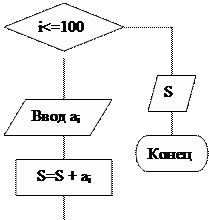
Вычислить сумму 100 чисел (рис. 5.2.7).

8.

Конец.

Рис. 5.2.7. Блок – схема к примеру 5.2.3 с циклом «Пока»

Цикл с постусловием («До»).

Тело цикла

В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет повторяться до тех пор, пока значение логического выражения ложно. Как только оно становится истинным, выполнение тела цикла прекращается (рис. 5.2.8).

Вход Истина

Рис. 5.2.8. Структура «цикла с постусловием».

Вывести максимальное значение из 100 натуральных чисел (рис. 5.2.9).

2.

Max=a1; i=2

max = ai

Ввести a1

b. ЕСЛИ maxai ТО max = ai

7. Вывести max.

Ложь Истина

Рис. 5.2.9. Блок – схема к примеру 5.2.4. с циклом «До»

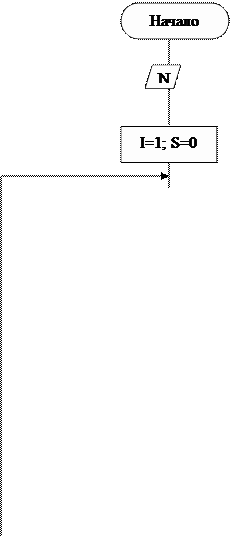
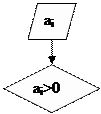
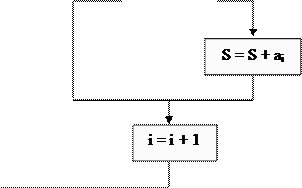
Базовые алгоритмические структуры можно комбинировать одну с другой – как путем организации их следования, так и путем создания суперпозиций (вложений одной структуры в другую). Используя описанные структуры, можно полностью исключить использование каких-либо еще операторов условного и безусловного перехода, что является важным признаком структурного программирования. Приведем несколько примеров (рис. 5.2.10, 5.2.11, 5.2.12, 5.2.13).

—

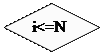
Рис. 5.2.10. Алгоритм типа «развилка, вложенная в цикл, с предусловием», для нахождения суммы положительных чисел и N возможных

— +

—

Рис. 5.2.11. Алгоритм типа «цикл, с предусловием, вложенный в неполную развилку»

— +

Рис. 5.2.12. Алгоритм типа «неполная развилка, вложенная в пол-

— + ную развилку».

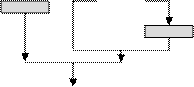Вопросы для самоконтроля

1. Дайте определение алгоритма и поясните его.

2. Какие формы представления алгоритма вы знаете?

3. В чем особенности графического представления алгоритма?

4. Назовите основные (базовые) алгоритмические структуры?

5. Перечислите свойства алгоритмов и объясните, чем они определены.

Статьи к прочтению:

Алгоритм

Похожие статьи:

1. Словесный. Такое описание алгоритма состоит из словесного перечня действий в виде предложений. Например, вычислить C= А-В, если А=В A + B , если A…

Для записи алгоритмов используют различные способы в зависимости от предназначения алгоритма. Рассмотрим следующие способы описания алгоритма:…

Источник