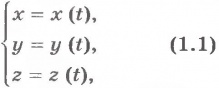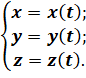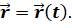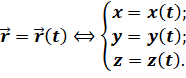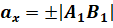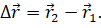Три способа описания движения материальной точки

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения

Теоретическая механика как наука. Три основных раздела ТМ. Кинематика. Основные задачи кинематики.

Теоретическая механика – наука об общих законах механических взаимодействий между материальными телами, а также об общих законах движения тел по отношению друг к другу.

Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику:

Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

Статика – это учение о равновесии совокупности тел некоторой системы отсчета.

Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Основная задача кинематики заключается в установлении (при помощи тех или иных математических методов) способов задания движения точек или тел и в определении по уравнениям их движений соответствующих кинематических характеристик движения, таких, как траектории, скорости и ускорения движущихся точек, угловые скорости и угловые ускорения вращающихся тел и др.

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения.

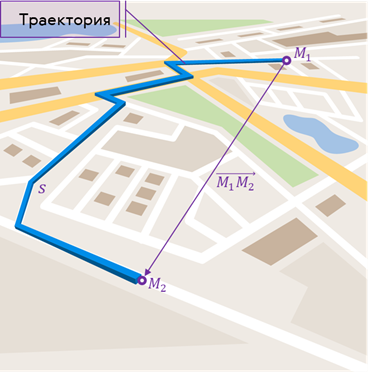
Естественный способ. Этим способом пользуются, если из­вестна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве.

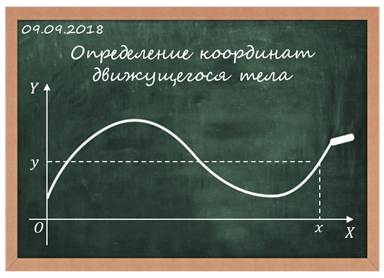
Координатный способ. Будем задавать положение точки с помощью координат. Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая — криволинейным.

Математически это принято записывать в виде:

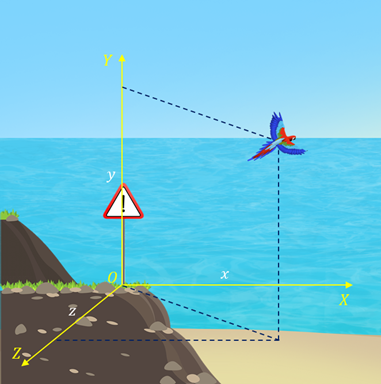
Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется, т. е. является функцией времени: r=r(t) (стрелочки над ними нужны). Одна такая функция равняется трем функциям (1.1). Если ввести единичные векторы i, j, k ( i = j = k = 1), направленные соответственно вдоль осей x, y и z то, очевидно, закон движения может быть представлен в виде:

r(t) = x(t)i + y(t)j + z(t)k.

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.

Источник

Видеоурок по физике «Способы описания движения. Траектория. Путь. Перемещение»

В этом видеоуроке мы с вами познакомимся с основными способами описания механического движения. Вспомним, какие существуют виды механического движения в зависимости от формы траектории. А также узнаем, что такое перемещение и чем оно отличается от пройдённого пути.

В начале урока напомним учащимся о том, что такое механическое движение. Механическим движением называется изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Для описания движения реального тела пользуются его моделью — материальной точкой, то есть телом, размерами и формой которого в данных условиях можно пренебречь.

Далее мы вводим два способа описания движения материальной точки: координатный и векторный.

При рассмотрении координатного способа описания движения следует обратить внимание учащихся на то, что при движении точки в выбранной системе отсчёта её координаты с течением времени изменяются. То есть они зависят от времени или, говорят, являются функциями времени.

Если уравнения движения известны, то мы можем рассчитать координаты точки для любого момента времени, а следовательно, и её положение относительно выбранного тела отсчёта.

Второй способ описания движения — векторный. В нём положение точки задаётся при помощи радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, как и координаты, является функцией времени, так как он изменяет свою длину и поворачивается.

Далее мы вводим понятие проекции вектора на ось и рассказываем, каким образом она определяется для различных случаев.

Также положение точки через некоторый промежуток времени можно определить, зная траекторию её движения, начальное положение точки на этой траектории и путь, пройденный точкой за этот промежуток времени. Далее мы напоминаем учащимся, что такое траектория движения, путь, и вводим понятие перемещения.

Здесь важно обратить внимание учащихся на то, что путь, пройденный телом, нельзя сравнивать с его перемещением, поскольку путь — величина скалярная, а перемещение — векторная.

В конце урока проводим краткое повторение изученного материала.

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Три способа описания движения материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

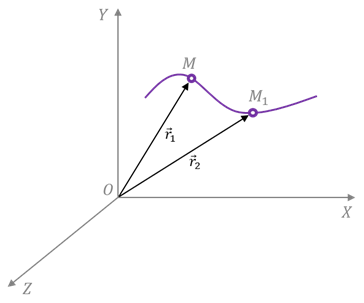
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

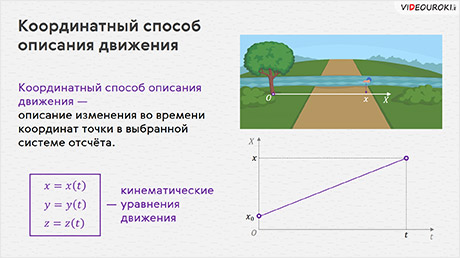
ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Способы описания движения. Траектория. Путь. Перемещение

Урок 2. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Способы описания движения. Траектория. Путь. Перемещение»

На прошлом уроке мы с вами говорили о механическом движении. Давайте вспомним, что механическим движением называется изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Теперь давайте вспомним, как рассчитывается положение точки в любой момент времени относительно выбранной системы отсчёта. Это можно сделать несколькими способами. Но мы пока рассмотри два — наиболее часто применяющиеся.

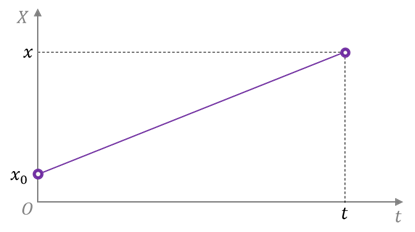
Первый способ — координатный. Очевидно, что при движении точки в выбранной системе отсчёта её координаты с течением времени изменяются. То есть они зависят от времени или, говорят, являются функциями времени:

Эти уравнения называются кинематическими уравнениями движения точки, записанными в координатной форме.

Если уравнения движения известны, то мы можем рассчитать координаты точки для любого момента времени, а следовательно, и её положение относительно выбранного тела отсчёта.

В зависимости от характера движения, положение точки может быть определено одной, двумя или тремя координатами. Так, например, для описания движения поезда нам достаточно связать с телом отсчёта систему координат, состоящую из одной координатной оси.

Однако при изучении движения тела на плоскости её уже будет недостаточно. В этом случае нам необходимо использовать систему координат с двумя взаимно перпендикулярными осями.

Соответственно, при рассмотрении движения тела в пространстве с телом отсчёта связывается система координат, состоящая из трёх взаимно перпендикулярных координатных осей.

Второй способ описания движения — векторный. В нём положение точки задаётся при помощи радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, как и координаты, является функцией времени, так как он изменяет свою длину и поворачивается:

Записанное уравнение является уравнением движения точки, записанным в векторном виде. Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.

Таким образом, задание трёх скалярных уравнений равносильно заданию одного векторного уравнения.

Однако при решении большинства задач используется понятие не вектора, а его проекции на ось координат.

Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Обозначать проекцию вектора будем той же буквой, что и вектор, но без стрелки над ней и с индексом внизу, указывающим, на какую ось проецируется вектор:

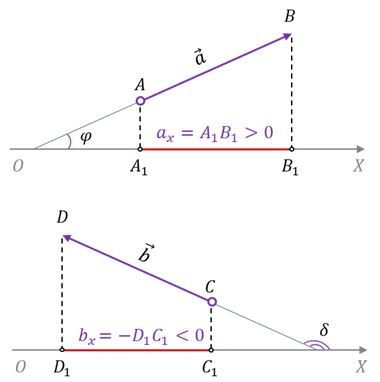
Давайте условимся, что проекцию вектора на ось мы будем брать со знаком «плюс», если направление вектора совпадает с направлением координатной оси́, на которую он проецируется. При этом обратите внимание: угол между вектором и координатной осью является острым. Соответственно, если направление вектора и координатной оси́ не совпадают, то проекцию вектора на эту ось будем брать со знаком «минус». Как видно из рисунка, в этом случае угол между вектором и осью координат является тупым.

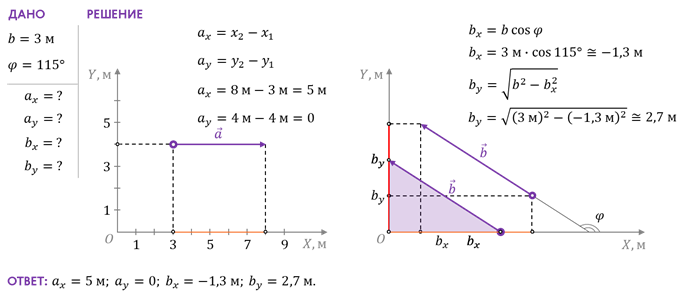
Для примера давайте определим проекции векторов а и b, представленных на рисунке. Модуль вектора b равен 3 м, а сам вектор направлен под углом 115 о к оси Х.

Так же положение точки через некоторый промежуток времени можно определить, зная траекторию её движения, начальное положение точки на этой траектории и путь, пройденный точкой за этот промежуток времени. Давайте с вами вспомним, что траекторией называется воображаемая линия, по которой движется точка в пространстве. А путь — это длина траектории, которую описала точка за время своего движения.

В зависимости от формы траектории любые движения точки можно разделить на прямолинейные и криволинейные. Здесь всё просто. Если траекторией является прямая линия, то движение прямолинейное, если кривая — криволинейное.

Однако, в случае, когда траектория движения точки неизвестна, её положение в некоторый момент времени определить невозможно. Например, пусть в некоторый момент времени наша материальная точка занимает в пространстве некоторое положение М₁. Вопрос: где окажется точка спустя некоторый промежуток времени после этого момента? Очевидно, что ответов на этот вопрос бесконечное множество, даже если знать, какой путь успела она пройти за этот промежуток времени. Следовательно, для ответа на этот вопрос нам необходимо знать ещё и направление, в котором двигалась точка, то есть знать её вектор перемещения или просто перемещение.

Перемещением называется вектор, проведённый из начального положения точки в её конечное положение.

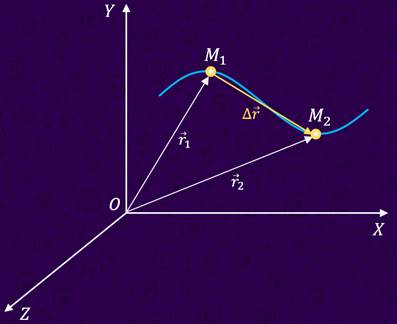
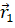
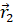
При векторном способе задания движения перемещение можно рассматривать как изменение радиус-вектора движущейся точки. Покажем это. Пусть в некоторый момент времени t­₁ положение точки задаётся радиус вектором . Соответственно, в момент времени t­₂ — радиус-вектором . Тогда, чтобы найти изменение радиус вектора за промежуток времени (t­₂ – t­₁), нужно из конечного вектора вычесть вектор начальный.

Из полученного рисунка видно, что перемещение, совершенное точкой за промежуток времени Δt, есть изменение её радиус-вектора за это время:

Теперь напомним важную деталь: путь, пройденный телом, нельзя сравнивать с его перемещением. Ведь путь — это величина скалярная, а перемещение — векторная. Поэтому сравнивать путь можно только с модулем перемещения. При этом следует помнить, что путь может быть равен модулю перемещения только в случае прямолинейного однонаправленного движения. Во всех остальных случаях путь всегда больше модуля перемещения.

Для примера решим такую задачу. Мальчик на роликах пересёк прямоугольную площадку по диагонали AB, а второй мальчик прошёл пешком из точки A в точку B по краю площадки. Определите модули перемещений обоих мальчиков и пути, пройденные ими, если размеры площадки 60 х 80 м.

В заключении урока рассмотрим опыт, описанный ещё в книге Галилея «Диалог о двух системах мира». Итак, у нас есть корабль, движущийся по реке, и два наблюдателя: на корабле и на берегу реки. С вершины мачты на палубу падает ядро. Для наблюдателя, находящегося на палубе, траекторией движения ядра является прямая линия. А путь и модуль перемещения ядра будут равны.

Однако с точки зрения наблюдателя, находящегося на берегу, ядро будет двигаться по ветке параболы, так как оно имеет некоторую начальную горизонтальную скорость, равную скорости корабля. Поэтому для него на берегу ядро будет двигаться по криволинейной траектории. А модуль его перемещения не будет равен пройденному пути.

Этот простой и очень наглядный пример говорит нам о том, что форма траектории, путь и перемещение тела зависят от выбора системы отсчёта.

Источник