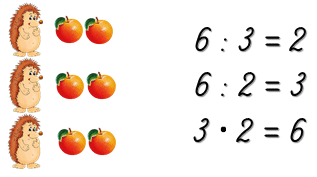Три способа деления 3 класс

Алгоритмы устных способов деления двузначных и трёхзначных чисел
консультация по математике (3 класс) на тему

Для успешного овладения учащимися 3-4 классов устным счётом я составила свои алгоритмы для некоторых случаев деления двузначных и трёхзначных чисел методом подбора.

Скачать:

Вложение	Размер
algoritmy.docx	14.28 КБ

Предварительный просмотр:

Для успешного овладения учащимися 3-4 классов устным счётом я составила свои алгоритмы для некоторых случаев деления двузначных и трёхзначных чисел методом подбора.

Алгоритмы устных способов деления двузначных и трёхзначных чисел

Алгоритм вычисления вида 48 : 2
Для того чтобы вычислить выражение вида 48 : 2, надо:
1) разделить единицы на делитель;
2) разделить десятки на делитель;
3) сложить полученные частные;
4) оформить результат вычисления.
Например: 48 : 2 = (8+40) : 2 = 8 : 2 + 40 : 2 = 4+20 = 24.

Алгоритм вычисления вида 57 : 3

Для того чтобы вычислить выражение вида 57 : 3, надо:
1) разделить единицы на делитель;
2) число 7 на 3 не делится, занимаем десяток;
3) число 17 на 3 не делится, занимаем ещё десяток;
4) число 27 на 3 делится, ответ 9;
5) разделить десятки на делитель, два занимали, осталось три десятка; 30 на 3 делится, ответ 10;
6) сложить полученные частные;
7) оформить результат вычисления.

Например: 57 : 3 = (27+30) : 3 = 27 : 3 + 30 : 3 = 9+10 = 19.

Алгоритм деления двузначного числа на двузначное число вида 72 : 18

Для того, чтобы разделить двузначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, при делении десятков на десятки получаются единицы, значит, в частном будет одна цифра;
2) делим единицы на единицы;
3) число 2 на 8 не делится, занимаем десяток;
4) число 12 на 8 не делится, занимаем ещё десяток;
5) число 22 на 8 не делится, занимаем ещё десяток;
6) число 32 на 8 делится, ответ 4;
5) делим десятки на десятки, 3 занимали, осталось 4 десятка; 4 на 1 делится, ответ тоже 4;
6) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;
7) делаем проверку.

Алгоритм деления двузначного числа на двузначное число вида 75 : 25

Для того, чтобы разделить двузначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, при делении десятков на десятки получаются единицы, значит в частном будет одна цифра;
2) делим единицы на единицы;
3) число 5 на 5 делится, ответ 1;
4) делим десятки на десятки, 7 на 2 не делится без остатка, значит ответ 1 не верный;
5) занимаем десяток, число 15 на 5 делится, ответ 3;
6) делим десятки на десятки, один занимали, осталось 6 десятков, 6 на 2 делится, ответ 3;
7) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;
8) делаем проверку.

Алгоритм деления трёхзначного числа на двузначное число вида 196 : 28

Для того, чтобы разделить трёхзначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, в частном будет одна цифра;
2) делим единицы на единицы, число 6 на 8 не делится, занимаем десяток;
3) число 16 на 8 делится, ответ 2;
4) делим десятки на десятки, один занимали, осталось 18 десятков, 18 на 2 делится, ответ 9;
5) сравниваем полученные ответы, они не совпадают, следовательно, частное определено не верно;
6) делим единицы на единицы, число 6 на 8 не делится, занимаем десятки;
7) 56 на 8 делится, ответ 7;
8) делим десятки на десятки, пять занимали, осталось 14, 14 на 2 делится, ответ 7.
9) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;

Источник

Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.

2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.

3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.

Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

Чтение числовых выражений

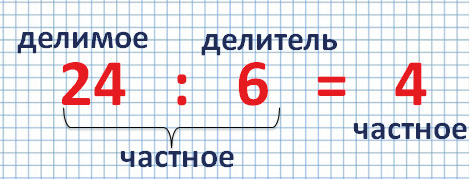
Этот пример можно прочитать по-разному.

• 24 разделить на 6 равняется 4.
• 24 уменьшить в 6 раз – получится 4.
• Делимое – 24, делитель – 6, частное – 4.
• Частное от деления числа 24 на 6 равно 4.

Деление на 1

Деление на 0

Деление числа само на себя

Связь деления и умножения

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Вывод: Если в задаче есть слова «в . раз меньше», то задача решается делением.

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Источник

Как объяснить ребенку деление столбиком во 2-3 классе

Как объяснить ребенку деление столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.

xvatit.com

Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?

Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:

• ребенок свободно выполняет операции сложения и вычитания;
• знает разряды чисел;
• знает назубок таблицу умножения.

Как объяснить ребенку смысл действия «деление»?

• Ребенку нужно объяснить все на наглядном примере.

Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.

Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.

• Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
• Объясните, что деление – это операция противоположная умножению, умножение наизнанку.

Удобно показать взаимосвязь деления и умножения на примере таблицы.

Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).

Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).

Компоненты при делении называются иначе:

12 — делимое;
3 — делитель;
4 — частное (результат деления).

Как объяснить ребенку деление двузначного числа на однозначное не в столбик?

Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?

Возьмем для примера 72:3.

Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.

Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).

72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.

После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

Как объяснить ребенку деление в столбик: алгоритм решения

Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:

• Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель

• Записать делимое — «уголок» — делитель.

• Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.

Рассуждаем так: 2 не делится на 3, значит — берем 21.

• Определить, сколько раз делитель «помещается» в выбранной части.

21 разделить на 3 — берем по 7.

• Умножить делитель на выбранное число, результат записать под «уголком».

7 умножить на 3 — получаем 21. Записываем.

На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.

• Повторить действия, пока в остатке не окажется 0.

Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.

Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком

Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.

2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.

6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!

7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!

Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.

Почему детям сложно научиться делить в столбик?

Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.

Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.

Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.

Предлагаем Вашему вниманию программы развивающих занятий с собаками- терапевтами в зависимости от возраста ребёнка и Ваших пожеланий:

• Тренинг по освобождению от страха собак. 3+
• Занятия с собаками-терапевтами «Почитай собаке». 5+
• Занятие для малышей «Собаки-обнимаки». 0+ (до 3 лет)
• Обучающее занятие «Детям о профессиях людских и собачьих». 4+
• Обучающие занятия с собаками-терапевтами в рамках творческого лагеря. 8+
• Занятия с собаками-терапевтами и детьми с нарушениями в развитии. 5+
• Развивающий курс «Собака — друг человека». (4 занятия). 4+

Источник