Трансцендентное уравнение способы решения

Численные методы решения трансцендентных уравнений

Трансцендентное уравнение: понятие и характеристика. Метод половинного деления (дихотомии), его сущность. Применение метода простой итерации для решения уравнения. Геометрический смысл метода Ньютона. Уравнение хорды и касательной, проходящей через точку.

Рубрика	Математика
Вид	курсовая работа
Язык	русский
Дата добавления	28.06.2013

Основной целью данной курсовой работы является изучение и сравнительный анализ численных методов решения трансцендентных уравнений.

В данной курсовой работе рассмотрено 5 методов решения трансцендентных уравнений.

Трансцендентными называются уравнения, не являющиеся алгебраическими. Т.е. содержащие функции (тригонометрические, показательные, логарифмические и др.).

Методы решения трансцендентных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения или в виде формулы. Итерационные методы являются приближенными методами.

2) Общая информация

3) Метод половинного деления (Дихотомии)

4) Метод простой итерации

6) Метод Ньютона (Метод касательных, линеаризации)

7) Метод хорд и касательных

Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например:

Более строгое определение таково:

Трансцендентное уравнение — это уравнение вида , где функции и являются аналитическими функциями, и по крайней мере одна из них не является алгебраической.

Актуальность этих методов с момента создания и по сей день присутствует во многих областях жизни человека.

Объект исследования — рассмотрение методов решения трансцендентных уравнений.

Поставлены следующие задачи:

— проанализировать приведенные методы;

— выбрать один из методов;

— создать контрольный вариант;

— реализовать алгоритм на языке программирования;

— проверить работоспособность алгоритма;

2. Общая информация

Алгебраические уравнения (в канонической форме):

аn x n + an-1 x n-1 + . + a1x + a0 = 0

Трансцендентные уравнения — в которых переменная х находится под знаком трансцендентной функции:

показательная а х ;

логарифмическая log a x ;

тригонометрические sin x ;

Решение нелинейного уравнения не всегда возможно и не всегда целесообразно, поэтому решение таких уравнений ведется приближённо.

Пусть существует такая непрерывная функция f(x) и требуется найти все или некоторые корни уравнения:

Допустим, существует такой корень x’ уравнения f(x)=0, что он сводит его в тождество f(x’)=0, тогда, решая уравнение каким-либо численным методом, мы находим приближённое значение корня x*, с погрешностью r. r — абсолютная погрешность.

Итак, во-первых, необходимо найти количество и расположение этих корней. Во-вторых, найти приближенные значения корней. В-третьих, выбрать из них необходимые нам корни, а также уточнить их приближённые значения. Первые две задачи можно решить аналитическими, либо графическими методами.

Для отделения корней существуют различные методы. Например, это может быть ясно из смысла задачи.

Если необходимо найти только действительные корни, есть смысл составить таблицу значений f(x). Если в двух соседних колонках таблицы находятся значения с разными знаками, то между ними существует нечетное число корней, по крайней мере, один корень. Если узлы близки, то, скорее всего, между ними всего один корень.

Но выявить по таблице корень четной кратности крайне сложно.

Также, возможно отделение корней с помощью построения графика функции y = f(x), где приближенные значения действительных корней уравнения f(x) = 0 соответствуют абсциссам точек пересечения или касания графика с осью 0x. Помимо этого, построение графика часто позволяет найти корни чётной кратности.

«Иногда удается заменить уравнение (1) эквивалентным ему уравнением ц(x)=ш(x), в котором функции y1= ц(x) и y2= ш(x) имеют несложные графики. Например, уравнение x*sin(x)-1=0 удобно преобразовать к виду sin(x)=1/x. Абсциссы точек пересечения этих графиков будут корнями исходного уравнения». Калиткин Н.Н. «Численные методы» стр.139

Но наиболее распространен следующий метод: если на концах некоторого интервала [a, b] значения непрерывной функции f(x) имеют разные знаки, то на этом интервале уравнение F(x)=0 имеет хотя бы один корень. При этом корень является единственным, если производная функции f'(x) существует и сохраняет свой знак внутри интервала [a, b].

3. Метод половинного деления (Дихотомии)

На мой взгляд, самый легкий метод. Он прост и очень надёжен. К простому корню метод дихотомии сходится для любых непрерывных функций, в том числе недифференцируемых. Он устойчив к ошибкам округления.

Его суть заключается в построении отрезков, но при этом на каждом шаге очередной отрезок делится пополам и в качестве следующего отрезка берется та половина, на которой значения функции в концах имеют разные знаки. Процесс продолжают до тех пор, пока длина очередного отрезка не станет меньше, чем величина 2е. Тогда его середина и будет приближенным значением корня с точностью е.

Для этого метода существенно, чтобы функция f(x) была непрерывна и ограничена в заданном интервале [a, b], внутри которого находится корень. Предполагается также, что значения функции на концах интервала f(a) и f(b) имеют разные знаки, т.е. выполняется условие f(a)f(b) .

Алгоритм данного метода можно записать так:

1.Ввести данные (a, b, е).

2.Если нужная точность достигнута (| b — a | 0), то в качестве следующего отрезка взять правую половину (а=c), иначе левую (b=c).

6.Напечатать ответ c=.

Метод половинного деления легко реализуется и является наиболее универсальным среди итерационных методов уточнения корней. Его применение гарантирует получение решения для любой непрерывной функции f(x), если найден интервал, на котором она изменяет знак. В том случае, когда корни не отделены, будет найден один из корней уравнения.

Метод всегда сходится, но скорость сходимости является небольшой, так как за одну итерацию точность увеличивается примерно в два раза. Однако существуют, иногда довольно значительные, недостатки метода половинного деления. Как уже говорилось выше, для того чтобы решить уравнение необходимо найти отрезок, на котором функция меняет свой знак. И если в этом отрезке не один корень, то неясно, к какому из корней сойдется метод (к одному корню сойдется точно). Также метод неприменим для корней чётной кратности. Наконец, не используется для систем уравнений.

Поэтому на практике метод половинного деления обычно применяется для грубого нахождения корней уравнения, поскольку при повышении требуемой точности значительно возрастает объем вычислений.

Один из минусов метода половинного деления (сходимость неизвестно к какому корню) имеется у всех итерационных методов, почти у всех. В таком случае может помочь только удаление ранее найденных корней. Однако, как я заметил, уменьшается точность методов.

Реализация удаления корней: « Если x1 есть простой корень уравнения f(x) непрерывна, то вспомогательная функция g(x)=f(x)/(x-x1) непрерывна, причем все нули функций f(x) и g(x) совпадают, за исключением x1, то он будет нулем g(x) кратности на единицу меньше; остальные нули обеих функций по-прежнему будут одинаковы». Калиткин Н.Н. «Численные методы» стр.140

Пример. Необходимо методом дихотомии уточнить корень уравнения х 3 — 3 х +1 = 0 с точностью 10 -3 (табл. 2) .

Источник

РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ. МЕТОДЫ РЕШЕНИЯ

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

1) Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.

2) Значения f(x) на концах отрезка имеют разные знаки (f(a)×f(b) (x) сохраняют определенный знак на всем отрезке.

Условия 1) и 2) гарантируют, что на интервале [a,b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.

Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.

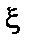
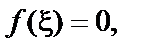Всякое значение , обращающее функцию f(x) в нуль, т.е. такое, что:

называется корнем уравнения (1) или нулем функции f(x).

Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:

1) отделение корней — отыскание приближенного значения корня или содержащего его отрезка;

2) уточнение приближенных корней — доведение их до заданной степени точности.

Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.

Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.

В инженерной практике распространен графический способ определения приближенных корней.

Графический метод отделения корней

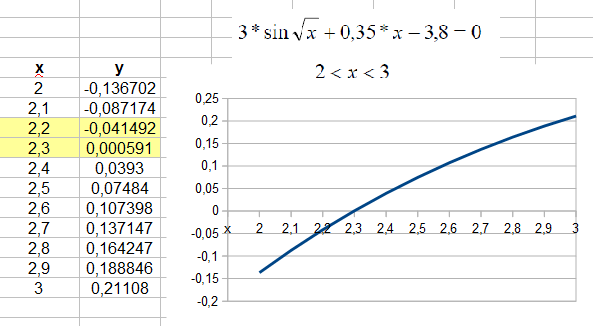
Для отделения корня графическим способом строится график функции f(x)=0 по таблице значений аргументов и функций, где аргумент изменяется с фиксированным шагом. Визуально определяют точку пересечения графика с осью OX. На этом интервале функция меняет знак отрицательный на положительный (рис.1).

Рис.1. Отделение корня графическим способом

Этот интервал изолируют как интервал с единственным возможным корнем. Уравнение может иметь несколько интервалов изоляций и, соответственно, несколько корней.

Рассмотрим методы уточнения приближенных корней в электронной таблице Calc. Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

1. подбора параметра;

2. метод простых итераций;

3. метод половинного деления (метод дихотомии);

4. метод Ньютона (метод касательных);

5. модифицированный метод Ньютона (метод секущих);

6. метод хорд и др.

Подбор параметра

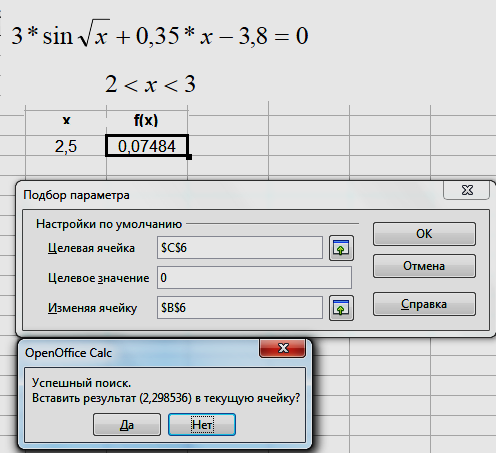
При подборе параметра OOo Calc изменяет значение в одной конкретной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат. Для реализации этого метода нужно в любую ячейку таблицы ввести значение х, принадлежащее интервалу [а,b] (т.е., в пределах отделенного корня). В следующую ячейку ввести значение функции f(x). Затем выбрать команду Сервис\Подбор параметра (рис.2.). В появившемся окне подбора параметра ввести:

• Ячейка с формулой – адрес ячейки с уравнением.

• Целевое значение – результат функции.

• Изменяемая ячейка – адрес ячейки, в которой находится переменная, т.е. х подбираемый из диапазона.

Программа Calc подбирает наиболее подходящий корень и вставляет его в изменяемую ячейку, т.е. вместо х.

Пример решения уравнения методом подбора параметра показан на рис.2.

Рис.2. Метод побора параметра

Дата добавления: 2016-06-15 ; просмотров: 13362 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник