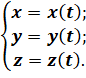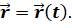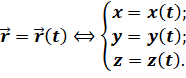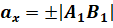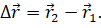Траекторный способ описания движения

Траекторный способ описания движения

В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.

1. Векторный способ.

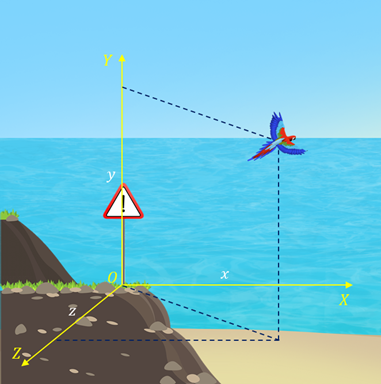
В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.

Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.

В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

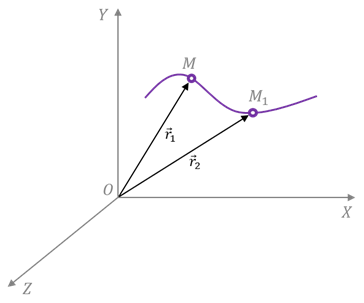
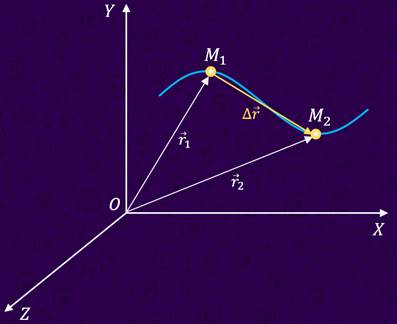
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.

Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.

Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_»cp»` тела за время `Delta t`:

`vecv_»cp»=(Deltavecr)/(Delta t)` (1)

Вектор `vecv_»cp»` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.

Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.

Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:

`vec v =(Delta vec r)/(Delta t)` при `Delta t -> 0`.

Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.

В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).

Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.

Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:

`vec a =(Delta vec v)/(Delta t)` при `Delta t -> 0` (2)

При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`»м»//»с»`) и метр на секунду в квадрате ( `»м»//»с»^2`).

2. Координатный способ.

В этом способе положение материальной точки `A` на плоскости в произвольный момент времени `t` определяется двумя координатами `x` и `y`, которые представляют собой проекции радиус-вектора $$ \overrightarrow$$тела на оси `Ox` и `Oy` соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями `t`: $$ x=x\left(t\right)$$ и $$ y=y\left(t\right)$$. Если эти функции известны, то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости $$ \overrightarrow$$ можно спроецировать на оси координат и определить таким образом скорости $$ _$$ и $$ _$$ изменения координат тела (рис. 4). В самом деле $$ _$$ и $$ _$$ будут равны значениям, к которым стремятся соответственно отношения `Delta x//Delta t` и `Delta y//Delta t` при стремлении к нулю промежутка времени `Delta t`.

3. Естественный (или траекторный) способ.

Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.

Движение тела определено, если известны его траектория, начало отсчёта `O`, положительное направление отсчёта дуговой координаты `l` и зависимость $$ l\left(t\right)$$.

Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь `Delta S` — это длина участка траектории, пройденного телом за промежуток времени `Delta t`.

Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.

Средней путевой скоростью `v_»cp»` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:

`v_»cp»=(Delta S)/(Delta t)` (3)

Определённая ранее средняя скорость `v_»cp»` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.

Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_»cp»` и средняя путевая скорость `v_»cp»` троллейбуса?

Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_»ср»=Deltavecr//Deltat=0` и `|vecv_»ср»|=0`. Но средняя путевая скорость троллейбуса не равна нулю:

`v_»cp»=(Delta S)/(Delta t)=(72 «км»)/(8 «ч»)=9 «км»//»ч»`.

Источник

Видеоурок по физике «Способы описания движения. Траектория. Путь. Перемещение»

В этом видеоуроке мы с вами познакомимся с основными способами описания механического движения. Вспомним, какие существуют виды механического движения в зависимости от формы траектории. А также узнаем, что такое перемещение и чем оно отличается от пройдённого пути.

В начале урока напомним учащимся о том, что такое механическое движение. Механическим движением называется изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Для описания движения реального тела пользуются его моделью — материальной точкой, то есть телом, размерами и формой которого в данных условиях можно пренебречь.

Далее мы вводим два способа описания движения материальной точки: координатный и векторный.

При рассмотрении координатного способа описания движения следует обратить внимание учащихся на то, что при движении точки в выбранной системе отсчёта её координаты с течением времени изменяются. То есть они зависят от времени или, говорят, являются функциями времени.

Если уравнения движения известны, то мы можем рассчитать координаты точки для любого момента времени, а следовательно, и её положение относительно выбранного тела отсчёта.

Второй способ описания движения — векторный. В нём положение точки задаётся при помощи радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, как и координаты, является функцией времени, так как он изменяет свою длину и поворачивается.

Далее мы вводим понятие проекции вектора на ось и рассказываем, каким образом она определяется для различных случаев.

Также положение точки через некоторый промежуток времени можно определить, зная траекторию её движения, начальное положение точки на этой траектории и путь, пройденный точкой за этот промежуток времени. Далее мы напоминаем учащимся, что такое траектория движения, путь, и вводим понятие перемещения.

Здесь важно обратить внимание учащихся на то, что путь, пройденный телом, нельзя сравнивать с его перемещением, поскольку путь — величина скалярная, а перемещение — векторная.

В конце урока проводим краткое повторение изученного материала.

Источник

Способы описания движения. Траектория. Путь. Перемещение

Урок 2. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Способы описания движения. Траектория. Путь. Перемещение»

На прошлом уроке мы с вами говорили о механическом движении. Давайте вспомним, что механическим движением называется изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Теперь давайте вспомним, как рассчитывается положение точки в любой момент времени относительно выбранной системы отсчёта. Это можно сделать несколькими способами. Но мы пока рассмотри два — наиболее часто применяющиеся.

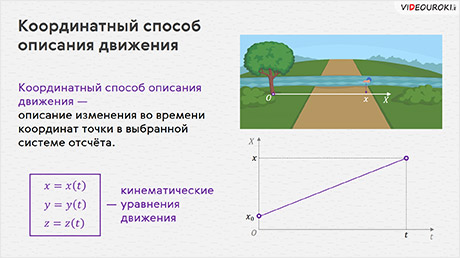
Первый способ — координатный. Очевидно, что при движении точки в выбранной системе отсчёта её координаты с течением времени изменяются. То есть они зависят от времени или, говорят, являются функциями времени:

Эти уравнения называются кинематическими уравнениями движения точки, записанными в координатной форме.

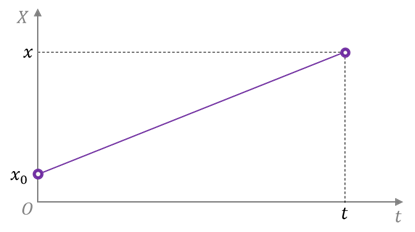
Если уравнения движения известны, то мы можем рассчитать координаты точки для любого момента времени, а следовательно, и её положение относительно выбранного тела отсчёта.

В зависимости от характера движения, положение точки может быть определено одной, двумя или тремя координатами. Так, например, для описания движения поезда нам достаточно связать с телом отсчёта систему координат, состоящую из одной координатной оси.

Однако при изучении движения тела на плоскости её уже будет недостаточно. В этом случае нам необходимо использовать систему координат с двумя взаимно перпендикулярными осями.

Соответственно, при рассмотрении движения тела в пространстве с телом отсчёта связывается система координат, состоящая из трёх взаимно перпендикулярных координатных осей.

Второй способ описания движения — векторный. В нём положение точки задаётся при помощи радиус-вектора.

Радиус-вектор — это направленный отрезок, проведённый из начала координат в данную точку.

При движении материальной точки радиус-вектор, как и координаты, является функцией времени, так как он изменяет свою длину и поворачивается:

Записанное уравнение является уравнением движения точки, записанным в векторном виде. Если оно известно, то мы можем для любого момента времени рассчитать радиус-вектор точки, а значит, определить её положение.

Таким образом, задание трёх скалярных уравнений равносильно заданию одного векторного уравнения.

Однако при решении большинства задач используется понятие не вектора, а его проекции на ось координат.

Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Обозначать проекцию вектора будем той же буквой, что и вектор, но без стрелки над ней и с индексом внизу, указывающим, на какую ось проецируется вектор:

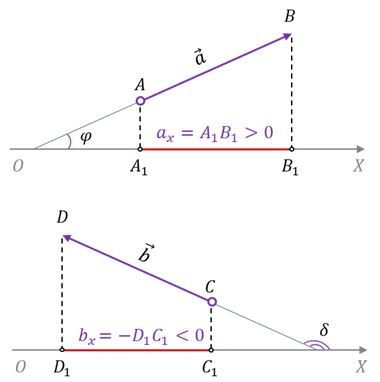
Давайте условимся, что проекцию вектора на ось мы будем брать со знаком «плюс», если направление вектора совпадает с направлением координатной оси́, на которую он проецируется. При этом обратите внимание: угол между вектором и координатной осью является острым. Соответственно, если направление вектора и координатной оси́ не совпадают, то проекцию вектора на эту ось будем брать со знаком «минус». Как видно из рисунка, в этом случае угол между вектором и осью координат является тупым.

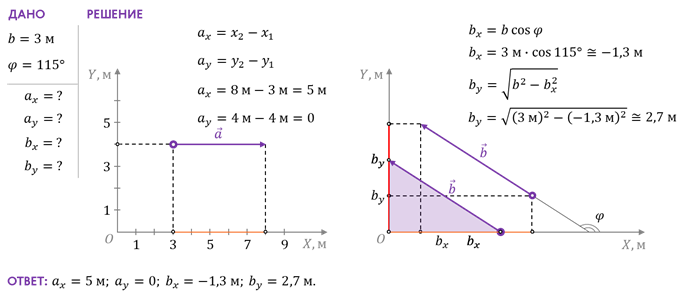
Для примера давайте определим проекции векторов а и b, представленных на рисунке. Модуль вектора b равен 3 м, а сам вектор направлен под углом 115 о к оси Х.

Так же положение точки через некоторый промежуток времени можно определить, зная траекторию её движения, начальное положение точки на этой траектории и путь, пройденный точкой за этот промежуток времени. Давайте с вами вспомним, что траекторией называется воображаемая линия, по которой движется точка в пространстве. А путь — это длина траектории, которую описала точка за время своего движения.

В зависимости от формы траектории любые движения точки можно разделить на прямолинейные и криволинейные. Здесь всё просто. Если траекторией является прямая линия, то движение прямолинейное, если кривая — криволинейное.

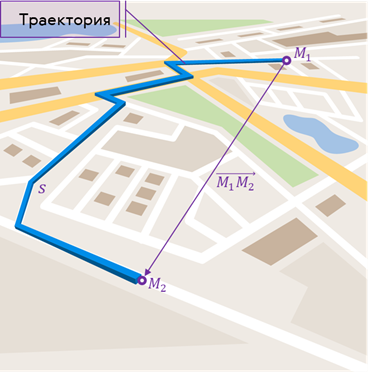
Однако, в случае, когда траектория движения точки неизвестна, её положение в некоторый момент времени определить невозможно. Например, пусть в некоторый момент времени наша материальная точка занимает в пространстве некоторое положение М₁. Вопрос: где окажется точка спустя некоторый промежуток времени после этого момента? Очевидно, что ответов на этот вопрос бесконечное множество, даже если знать, какой путь успела она пройти за этот промежуток времени. Следовательно, для ответа на этот вопрос нам необходимо знать ещё и направление, в котором двигалась точка, то есть знать её вектор перемещения или просто перемещение.

Перемещением называется вектор, проведённый из начального положения точки в её конечное положение.

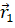
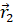
При векторном способе задания движения перемещение можно рассматривать как изменение радиус-вектора движущейся точки. Покажем это. Пусть в некоторый момент времени t­₁ положение точки задаётся радиус вектором . Соответственно, в момент времени t­₂ — радиус-вектором . Тогда, чтобы найти изменение радиус вектора за промежуток времени (t­₂ – t­₁), нужно из конечного вектора вычесть вектор начальный.

Из полученного рисунка видно, что перемещение, совершенное точкой за промежуток времени Δt, есть изменение её радиус-вектора за это время:

Теперь напомним важную деталь: путь, пройденный телом, нельзя сравнивать с его перемещением. Ведь путь — это величина скалярная, а перемещение — векторная. Поэтому сравнивать путь можно только с модулем перемещения. При этом следует помнить, что путь может быть равен модулю перемещения только в случае прямолинейного однонаправленного движения. Во всех остальных случаях путь всегда больше модуля перемещения.

Для примера решим такую задачу. Мальчик на роликах пересёк прямоугольную площадку по диагонали AB, а второй мальчик прошёл пешком из точки A в точку B по краю площадки. Определите модули перемещений обоих мальчиков и пути, пройденные ими, если размеры площадки 60 х 80 м.

В заключении урока рассмотрим опыт, описанный ещё в книге Галилея «Диалог о двух системах мира». Итак, у нас есть корабль, движущийся по реке, и два наблюдателя: на корабле и на берегу реки. С вершины мачты на палубу падает ядро. Для наблюдателя, находящегося на палубе, траекторией движения ядра является прямая линия. А путь и модуль перемещения ядра будут равны.

Однако с точки зрения наблюдателя, находящегося на берегу, ядро будет двигаться по ветке параболы, так как оно имеет некоторую начальную горизонтальную скорость, равную скорости корабля. Поэтому для него на берегу ядро будет двигаться по криволинейной траектории. А модуль его перемещения не будет равен пройденному пути.

Этот простой и очень наглядный пример говорит нам о том, что форма траектории, путь и перемещение тела зависят от выбора системы отсчёта.

Источник