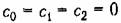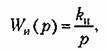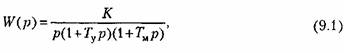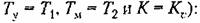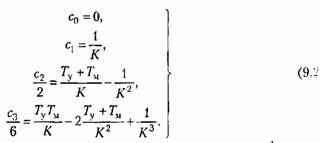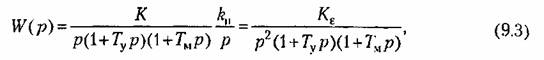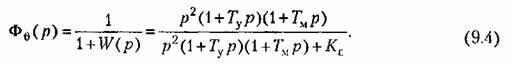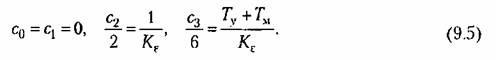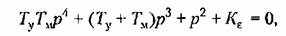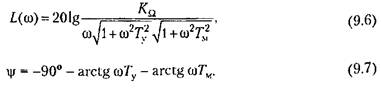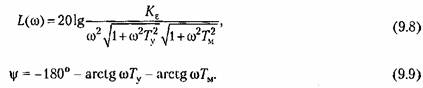Точность систем автоматического регулирования способы повышения

Повышение точности систем автоматического управления

К числу общих методов повышения точности систем автоматического управления относятся:

увеличение коэффициента передачи разомкнутой системы;

повышение порядка астат из м а;

применение управления по производным от ошибки.

Увеличение коэффициента передачи разомкнутой системы является наиболее универсальным и эффективным методом. Увеличить коэффициент передачи можно обычно за счет введения в систему усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.

Увеличение коэффициента передачи благоприятно сказывается в смысле уменьшения ошибок практически во всех типовых режимах. Это вытекает, в частности, из того, что он входит в качестве делителя во все коэффициенты ошибок (см. пример, рассмотренный в § 8.3).

Однако увеличение коэффициента передачи ограничивается устойчивостью системы. При повышении коэффициента передачи, как правило, система приближается к колебательной границе устойчивости. При некотором предельном его значении в системе возникают незатухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы управления.

В связи с этим повышение коэффициента передачи до значения, при котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повышении запаса устойчивости системы, что осуществляется при помощи так называемых корректирующих средств, рассматриваемых в следующей главе.

при астатизме перво-

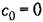
астатизме третьего порядка и т. д. Физически повышение порядка астатизма осуществляется за счет введения в канал системы интегрирующих звеньев. В качестве таких звеньев могут, например, использоваться звенья, изображенные на рис. 4.18.

Структурная схема системы с введенным интегрирующим звеном изображена на рис. 9.1. Передаточная функция интегрирующего звена

представляет собой

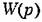
передаточную функцию разомкнутой системы управления до введения интегрирующего звена.

Результирующая передаточная функция разомкнутой системы будет иметь дополнительный множитель р в знаменателе:

Повышение порядка астатизма неблагоприятно сказывается на устойчивости системы. Поэтому одновременно с повышением порядка астатизма приходится использовать корректирующие звенья, повышающие запас устойчивости (см. главу 10). В качестве иллюстрирующего примера рассмотрим систему, изображенную на рис. 6.4, Для нее была получена передаточная функция разомкнутой системы в виде

которая соответствует астатизму первого порядка.

который дает интегрирующее

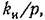
звено. В результате получим передаточную функцию разомкнутой системы в виде

— добротность системы по ускорению.

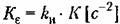
Эта передаточная функция соответствует уже астатизму второго порядка. Передаточная функция системы по ошибке

Раскладывая эту функцию в ряд делением числителя па знаменатель, получаем вместо (9.2) следующие равенства для коэффициентов ошибок:

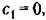
и, следовательно, будет равна нулю скоростная составляющая ошибки.

Это называется структурной неустойчивостью. Действительно, передаточной функции (9.3) соответствует характеристическое уравнение

в котором отсутствует член, содержащий оператор р в первой степени. Пропуск одного из членов в характеристическом уравнении всегда соответствует неустойчивости в соответствии с § 6.1.

Появление неустойчивости в рассматриваемой системе при повышении порядка астатизма можно проиллюстрировать па логарифмических характеристиках. Для передаточной функции (9.1) они построены на рис. 9.3, а по выражениям:

Логарифмические характеристики для передаточной функции (9.3) построены на рис. 9.3, б по выражениям:

. Однако это не означает, что схема является вообще неработоспособной. Введение в нее корректирующих средств (см. главу 10) позволяет не только достичь устойчивости, но и обеспечить определенный запас устойчивости, т. е. выполнить требования к качеству процесса управления.

Источник

Методы повышения точности системы

ИССЛЕДОВАНИЕ ТОЧНОСТИ САУ В УСТАНОВИВШЕМСЯ РЕЖИМЕ

Целью работы является исследование точности регулирования систем автоматического управления в установившемся режиме и изучение методов ее повышения.

Общие понятия

Исследование точности регулирования систем автоматического управления проводят путем анализа установившихся режимов ее функционирования. Ошибка регулирования 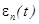для линейной системы, функциональная схема которой приведена на рис.2.1, определяется следующим образом

, (1)

где g(t) – задающее воздействие;

x(t) – выходной сигнал системы.

А в области изображений S уравнение (1) запишется как

. (2)

Связь между задающим воздействием g(t), возмущающим фактором z(t) и выходным сигналом системы x(t) в области изображений S устанавливается с помощью передаточных функций.

, (3)

где Wgx(S) – передаточная функция замкнутой системы по задающему воздействию g(t);

Wzx(S) — передаточная функция замкнутой системы по возмущающему фактору Z(t).

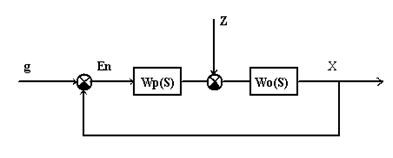
Для данной системы регулирования (рис.1) передаточные функции имеют вид

, (4)

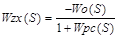
где передаточная функция разомкнутой системы;

Wp(S) — передаточная функция регулятора;

Wo(S) — передаточная функция объекта.

Подставляя выражения (3), (4) в (2) ,имеем

(5)

Следовательно, полная ошибка регулирования Eп(S) состоит из 2 составляющих

, (6)

где — ошибка регулирования, вызванная задающим воздействием g(t) ;

— ошибка регулирования, вызванная возмущающим фактором z(t).

Из выражений (5), (6) следует, что

(7)

, (8)

где — передаточная функция замкнутой системы по ошибке регулирования.

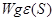
Используя выражения (6) и(8) и теорему о предельных значениях , при типовых воздействиях , установившиеся ошибки системы можно определить по следующим выражениям:

(9)

(10)

(11)

где — установившееся значение полной ошибки

— установившееся значение ошибки, вызванной задающим воздействием;

— установившееся значение ошибки, вызванной возмущающим фактором.

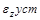
Уравнения (9)-(11) являются уравнениями статики, которые в статическом стационарном режиме ( ) связывают значения установившихся ошибок регулирования со значениями передаточных функций, определяемых при s=0. Первую составляющую полной ошибки регулирования можно свести к нулю путем масштабирования. Тогда точность системы регулирования будет полностью характеризоваться статической ошибкой

Методы повышения точности системы

Значение передаточной функции разомкнутой системы в стационарном режиме (s=0) определяется ее коэффициентом передачи . Поэтому из анализа выражения (5) вытекает один из методов повышения точности САУ-увеличение коэффициента .

Другим методом уменьшения ошибки регулирования является повышение астатизма системы. Данный метод позволяет устранить установившиеся ошибки при типовых воздействиях. Реализация астатизма путем введения интегрирующих звеньев приведена на рис.2.2. ПИ-регулятор системы обеспечивает ей астатизм 1 порядка, так как передаточная функция разомкнутой системы в общем виде имеет вид

(12)

где T= — постоянная форсирующей цепи;

— числитель и знаменатель передаточной функции объекта управления .

Повысить точность процесса регулирования системы возможно путем использования теории инвариантности. САУ является инвариантной по отношению к возмущающему воздействию z(t), если после окончания переходного процесса, определяемого начальными условиями, регулируемая величина x(t) и ошибка системы не зависят от этого воздействия.

САУ является инвариантной по отношению к управляющему воздействию g(t), если после окончания переходного процесса, определяемого начальными условиями, ошибка системы не зависит от этого воздействия. Оба эти определения имеют одну и ту же математическую трактовку и для обеспечения абсолютной инвариантности системы необходимо выполнение следующего условия

(13)Реализовать условие (13) можно, используя принцип двухканальности, когда используется и принцип регулирования по отклонению, и принцип управления по задающему g(t) либо возмущающему z(t) воздействию. В структурной схеме САУ с комбинированным управлением (рис.2.3) канал с регулятором по возмущению Wpz(S) реализует управление по возмущающему воздействию.

Рис. 2.3

Программа работы.

1.Набрать согласно рис 2.4 схему моделирования системы автоматического регулирования второго порядка.

Примечание: Модель П-регулятора W(S)=K1 набрать на отдельном линейном блоке.

2..Выставить задающее воздействие g(t)=0, возмущающий фактор Z(t)=Zo*1(t), 5В Zo 10В

Примечание: сигнал Z(t) получить от источника эталонного сигнала, измерив предварительно Zo на цифровом вольтметре.

3.Получить на экране индикатора и зарисовать выходной сигнал x(t) и сигнал ошибки от возмущающего фактора

Примечание: Вход индикатора “x” выбрать равным “10”, вход индикатора “Y” – “5”.

4.Провести исследование системы с П-регулятором (рис.2.4). 4.1 Снять для коэффициента П-регулятора K1, равного 1,0; 2,5; 5,0; 7,5; 10., установившееся значение ошибки по возмущающему фактору и построить зависимость .

4.2 Получить выражение передаточной функции замкнутой системы по возмущающему фактору в стационарном режиме Wzx(0).

4.3 Используя выражение (11), рассчитать для значений K1, указанных в п 4.1 и построить зависимость Сравнить полученные результаты с пунктом 4.1 и оценить влияние К1.

5. Провести исследование системы с ПИ-регулятором по схеме, приведенной на рис.2.5.

Примечание:Модель интегратора “ 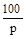” ПИ-регулятора набрать на отдельном линейном блоке, а его выходной сигнал подать насумматор линейного блока, на котором была реализована в п.1 модель П-регулятора..

Рис. 2.6

5.1 Зарисовать с экрана индикатора сигнал ошибки регулирования от возмущающего фактора Объяснить почему установившееся значение ошибки стремится к нулю?

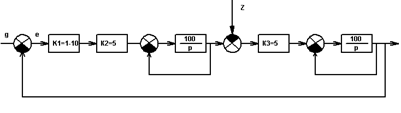
6.Провести исследование системы с комбинированным принципом управления, схема моделирования которой приведена на рис.2.6.

6.1 Используя условие инвариантности (13), определить выражение передаточной функции регулятора по возмущению Wpz(S), компенсирующего установившуюся ошибку регулирования .

6.2 Набрать с учетом полученного выражения Wpz(0). модель системы с комбинированным принципом управления (рис.2.6)

6.3 Зарисовать с экрана индикатора сигнал ошибки регулирования по возмущающему фактору .

6.4 Записать выражение сигнала от возмущающего фактора Xz, снимаемого с 4-го сумматора, обьяснить, почему установившаяся ошибка стремится к нулю.

1. Обьяснить ограниченность использования метода повышения точности САУ увеличением коэффициента усиления разомкнутой системы Kрс.

2. Недостатки метода повышения точности системы введением интегрирующих звеньев.

Источник