Точка прямая луч отрезок способы обозначения

Основы геометрии

Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.

Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.

Точка

Точка — это основная и самая простая геометрическая фигура.

В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.

В тексте точку обозначают следующим символом: « (·) A » — точка « А ».

Прямая

Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.

Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.

• Через две точки можно провести единственную прямую.
• Две прямые могут пересекаться только в одной точке.
• Через одну точку можно провести бесконечное множество прямых.

Способы обозначения прямых

• Строчной латинской буквой:

Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой.

Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча есть начало , но нет конца .

Способы обозначения лучей

• Строчной латинской буквой:

Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а вторая точка лежит на луче.

Отрезок

Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало , и конец .

Основное свойство отрезка — это его длина.

Длина отрезка — это расстояние между его концами.

В математике отрезок обозначается заглавными латинскими буквами.

Ломаная

Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.

Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.

Звенья ломаной — это отрезки ломаной.

В математике ломаная обозначается заглавными латинскими буквами.

Ломаная « ABCD ».
Вершины ломаной — A, B, C, D .
Звенья ломаной — AB, BC, CD.

Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.

KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см

Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.

Источник

Точки, прямые и отрезок

Для изображения на рисунке прямой мы пользуемся линейкой, но мы изображаем не всю прямую, а только лишь её кусок. Так как прямая в нашем представлении простирается до бесконечности в обе стороны, то прямая есть бесконечна.

На рисунке представленном выше мы видим, что точки А и С расположены на прямой а. В таких случаях говорят, что точки А и С принадлежат прямой а. Либо говорят, что прямая проходит через точки А и С. При записи принадлежность точки к прямой обозначают специальным значком. А тот факт, что точка не принадлежит прямой, отмечают таким же значком, только зачеркнутым.

В нашем случае точки B и D не принадлежат прямой а.

Как уже отмечалось выше, на рисунке точки А и С принадлежат прямой а. Часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными точками называется отрезком. Другими словами, отрезком называется часть прямой, ограниченная двумя точками.

В нашем случае мы имеем отрезок АB. Точки А и B называются концами отрезка. Для того, чтобы обозначить отрезок указывают его концы, в нашем случае АB. Одним из основных свойств принадлежности точек и прямых является следующее свойство: через любые две точки можно провести прямую, и притом только одну.

Если две прямые имеют общую точку, то говорят, что эти две прямые пересекаются. На рисунке прямые a и b пересекаются в точке A. Прямые а и с не пересекаются.

Любые две прямые имеют только одну общую точку либо не имеют общих точек. Если предположить обратное, что две прямые имеют две общих точки, тогда через них проходили бы две прямые. А это невозможно, так как через две точки можно провести лишь одну прямую.

Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.

Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча.

Если взять произвольную прямую a, и отметим на ней некоторую точку О, то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.

Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k.

Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.

На рисунке представлен луч ОС.

Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.

Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми.

Понятие и виды углов

Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О, и сторонами k и m.

На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.

Развернутый и неразвернутый угол

Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.

Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.

В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).

На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.

Измерение углов

Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.

В зависимости от градусной меры углы делятся на несколько групп.

1. Острый угол — градусная мера от 0 до 90 градусов.

2. Прямой угол — градусная мера 90 градусов.

3. Тупой угол — градусная мера больше 90 градусов.

Источник

Точки, Прямые и Отрезки — Определения и Свойства

Вспомним определения точки и прямой:

Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.

Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.

Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.

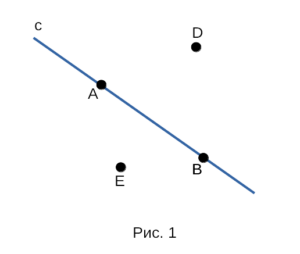
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.

Через любые две точки можно провести прямую,
и притом только одну.

Если две прямые имеют общую точку, то можно сказать,
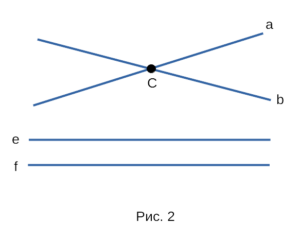
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.

Две прямые имеют только одну общую точку,
либо не имеют общих точек.

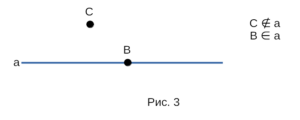
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.

Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

На рисунке изображена прямая a и точки D, F, G и H . Точки F и G лежат на прямой a . Точки D и H не лежат на прямой a .

В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.

Задача № 1 из учебника Атанасян 7-9 класс

Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .

Решение задачи

Обозначим её буквой a .

Отметим точки (·)A и (·)B , лежащие на прямой a .

Отметим точки (·)P, (·)Q и (·)R , не лежащие на прямой a .

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

На рисунке прямые a и b не пересекаются . Прямые b и c пересекаются .

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

В тексте пересечение прямых обозначают символом ∩ . Информацию на рисунке выше можно записать следующим образом:

• b ∩ c — прямые b и с пересекаются;
• a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M . Другими словами, прямые пересекаются в точке M . Геометрическими обозначениями пересечение прямых в точке записывается так:
e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через любые две точки можно провести прямую, и притом только одну .

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M .

Третий случай расположения прямых

Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B .

Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно .

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Теперь прямая a пересекается с прямой b , прямая b пересекается с прямой c и прямая c пересекается с прямой a .

В этом случае у нас только одна точка пересечения всех прямых — точка (·)D .

Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D . Тогда получится три точки пересечения — (·)D, (·)E и (·)F .

Прямая a пересекается с прямой b в точке (·)D , прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E . Условие задачи выполнено.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T .

Сам отрезок можно назвать ST или TS . Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник