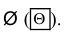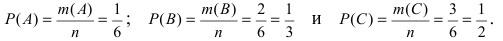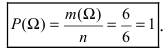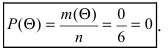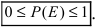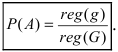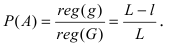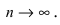То при выбранном способе оценки вероятности

Определения вероятности событий — вычисление с примерами решения

Содержание:

Основные понятия теории вероятностей:

1. Предмет теории вероятностей.

Теория вероятностей — это математическая дисциплина, которая устанавливает взаимозависимость между случайными величинами в случайных массовых процессах. Одним из основных понятий в теории вероятностей является понятие случайного события.

Определение: Случайным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти.

Например, при подбрасывании монеты нельзя угадать заранее, что выпадет: “решка” (аверс) или “орел” (реверс). Каждое из этих событий является простым и не может быть выражено через более простые события.

Определение: Элементарным событием называется событие, которое в результате проведения эксперимента может произойти или не произойти, а также не может быть представлено посредством более простых событий.

В теории вероятностей случайные элементарные события принято обозначать заглавными начальными буквами латинского алфавита

Определение: Сложным случайным событием называется событие, которое состоит из осуществления двух или более элементарных событий.

Определение: Эксперимент — это создание заранее заданного комплекса условий. Например, при подбрасывании монеты создают следующие условия: стол, на который падает монета, должен быть ровным, гладким, достаточно большим по площади, чтобы монета не могла скатиться.

Определение: Достоверным событием называется такое событие, которое обязательно произойдет в рамках данного опыта. Достоверное событие обозначается

Определение: Невозможным событием называется такое событие, которое ни при каких условиях не может произойти.

Невозможное событие обозначается

Например, совокупность выигрыша, проигрыша и ничья в шахматной партии образуют достоверное совокупное событие, т.е. одно из этих событий обязательно произойдет при игре в шахматы. При бросании кубика выпадение грани с 7 очками является невозможным событием.

Определение: Совместными событиями называются события, которые могут одновременно произойти в рамках данного опыта, все другие события называются несовместными.

Например, при бросании кубика выпадение грани с 4 очками (событие А) и выпадение четной грани (событие В) являются совместными событиями, а выпадение грани с 3 очками (событие А) и выпадение четной грани (событие В) являются несовместными событиями.

Определение: Полной группой случайных событий называется совокупность таких несовместных событий, что в результате проведения эксперимента хотя бы одно из них обязательно произойдет.

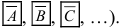
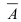
Определение: Противоположными событиями называются такие несовместные события, которые образуют полную группу (обозначаются Например, если событие А состоит в попадании снаряда в цель, то событие состоит в том, что снаряд не попадет в цель.

Замечание: Если в словесном описании случайного события присутствуют слова “хотя бы один”, то такое событие противоположно событию, содержащему в своем словесном описании слова “ни один”.

Определение: Равновозможными событиями называются такие случайные события, которые в условиях эксперимента имеют объективно равные шансы не произойти или произойти.

Например, однородность материала кости и несмещенность центра тяжести кубика являются теми условиями, при которых объективно возможно выпадение любой грани кубика.

Способы определения вероятности событий

Существуют два способа определения вероятности события

1. Теоретический способ основан на непосредственном (без проведения специального эксперимента) определении вероятности события по формуле: P(A)=m/n.
2. Статистический способ основан на предварительном прове­дении большого числа испытаний. При этом подсчитывают вероят­ность по формуле: h (A) = k / L.

Классическое определение вероятности

Определение: Вероятностью события называется численная мера степени объективной возможности случайного события.

Классическое определение вероятности применяется для нахождения вероятности конечного числа несовместных и равновозможных событии, образующих полную группу.

Пример №1

Пусть в урне находится 6 шаров: 1 белый, 2 красных и 3 синих. Опыт состоит в том, что из урны наудачу извлекают один шар. Определить полную группу случайных событий и наиболее вероятное событие.

Решение:

Для данного опыта полная группа событий состоит из 6 равновозможных исходов. Обозначим через А событие, состоящее в том, что из урны извлекают белый шар; В — красный шар; С — синий шар. Очевидно, событие С является более объективно возможным событием, чем события А и В, так как синих шаров в урне больше, чем белых и красных.

Классическое определение вероятности состоит в следующем:

Определение: Вероятностью случайного элементарного события называется отношение числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу.

В Примере число исходов, благоприятствующих извлечению белого шара, равно m(А) = 1, красного шара — m(В) = 2 и синего шара — m(С) = 3. Общее число всех равновозможных, несовместных, элементарных исходов, образующих полную группу, равно числу шаров в урне, т.е. n = 6. Таким образом, вероятности извлечь из урны тот или иной шар равны отношению числа элементарных исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных, несовместных, элементарных исходов, образующих полную группу:

В силу того,что события А, В и С образуют достоверное совокупное событие, то 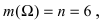следовательно, вероятность достоверного события равна:

Если в рассматриваемом Примере. обозначить через D событие, состоящее в том, что из урны извлекают черный шар, то этому событию благоприятствует нуль исходов (m(D) = 0), так как в урне нет черных шаров. Следовательно, событие D является невозможным событием О, а его вероятность равна:

Из рассмотренного Примере. видно, что вероятности всех событий есть положительные величины, которые принимают значения между вероятностью невозможного (0) и вероятностью достоверного (1) событий, т.е.

Замечание: Вероятность любого случайного события есть безразмерная и положительная величина, принимающая значения из промежутка от 0 до 1. Чем ближе вероятность события к нулю, тем меньше его возможность появления в данном опыте. Чем ближе вероятность события к единице, тем выше его возможность появления в данном эксперименте.

Геометрический способ определения вероятности

Геометрическое определение вероятности применяется для вычисления вероятности бесконечного числа несовместных и равновозможных событий, образующих полную группу.

Пусть имеется некоторая область G, которая может быть представлена в виде линии, площади или объема. Внутри области G находится другая область g, внутрь которой должна попасть точка, наудачу брошенная в область G. Пусть событие А состоит в том, что при попадании в область g включается лампочка, а при попадании в область G лампочка не загорается. Обозначим размеры областей g и G через 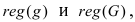соответственно. Появлению события А благоприятствует размер области g, а размер области G определяет общее число возможных исходов, следовательно, вероятность появления события А равна

Пример №2

Пусть на нити длиной L подвешен груз. Определить вероятность разрыва нити в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l.

Решение:

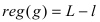
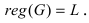
Пусть событие А состоит в том, что нить разорвется в любой точке, отстоящей от точки подвеса не менее чем на расстоянии l. Появлению этого события благоприятствуют все точки нити длиной L-l, т.е. , а длина всей нити равна L, т.е. Согласно геометрическому определению вероятности вероятность появления события А равна

Статистический способ определения вероятности событий

Данный способ определения вероятности событий применяется тогда, когда неприменимы два вышеприведенных способа. В основу данного способа положена устойчивость частоты появления изучаемого события при достаточно большом числе проводимых опытов, т.е. P(A) = v(A). При небольшом числе испытаний частота носит случайный характер, но при 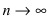она стабилизируется возле некоторого положения, характеризующего связь между комплексом условий и наблюдаемым событием (Рис. 1).

Рис. 1. Стабилизация частоты появления случайного события при

Косвенный способ определения вероятности событий

Данный способ определения вероятности событий применяется тогда, когда неприменимы три вышеприведенных способа. Он основан на теоремах теории вероятностей, которые рассматриваются ниже.

Рекомендую подробно изучить предметы:

Теория вероятностей Математическая статистика

Ещё лекции с примерами решения и объяснением:

• Предельные теоремы теории вероятностей
• Точечные оценки, свойства оценок
• Доверительный интервал для вероятности события
• Проверка гипотезы о равенстве вероятностей
• Многомерные случайные величины
• Случайные события — определение и вычисление
• Системы случайных величин
• Вероятность и риск

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Методы для оценки величины вероятностей и рисков

№	Методы оценки рисков	Суть метода
1.	Статистические методы	Суть статистических методов оценки риска заключается в определении вероятности возникновения потерь на основе статистических данных предшествующего периода.
1.1	Метод оценки вероятности исполнения	Позволяет дать упрощенную статистическую оценку вероятности исполнения какого – либо решения путем расчета доли выполненных и невыполненных решений в общей сумме принятых решений
1.2	Метод анализа вероятностных распределений потоков платежей	Позволяет при известном распределении вероятностей для каждого элемента потока платежей оценить возможные отклонения стоимостей потоков платежей от ожидаемых
1.3	Технология «Risk Metrics»	Разработана компанией «J.P. Morgan» для оценки риска рынка ценных бумаг. Методика подразумевает определение степени влияния риска на событие через вычисление «меры риска»
Аналитические методы	Позволяют определить вероятность возникновения потерь на основе математических моделей и используются в основном для анализа риска инвестиционных проектов.
2.1	Анализ чувствительности	Сводится к исследованию зависимости некоторого результирующего показателя от вариации значений показателей, участвующих в его определении
2.2	Метод корректировки нормы дисконта с учетом риска	Основная идея заключается в корректировке некоторой базовой нормы дисконта, которая считается безрисковой или минимально приемлемой
2.3	Метод достоверных эквивалентов	С помощью данного метода осуществляется корректировка ожидаемых значений потока платежей путем введения специальных понижающих коэффициентов (а) с целью приведения ожидаемых поступлений к величинам платежей, получение которых практически не вызывает сомнений и значения которых могут быть достоверно определены
2.4	Метод сценариев	Позволяет совместить исследование чувствительности результирующего показателя с анализом вероятностных оценок его отклонений
3.	Метод экспертных оценок	Представляет собой комплекс логических и математико – статистических методов и процедур по обработке результатов опроса группы экспертов, причем результаты опроса являются единственным источником информации
Метод аналогов	используется в том случае, когда применение иных методов по каким – либо причинам неприемлемо. Метод использует базу данных аналогичных объектов для выявления общих зависимостей и переноса их на исследуемый объект.

К вероятностям, используемым при определении количественной оценки риска, относятся вероятности событий и вероятности изменения состояния системы, в том числе вероятности безотказной работы оборудования.

При оценке вероятности существуют общие ошибки или смещения величин риска, которых следует избегать, учитывая следующие особенности.

— Обычно люди недооценивают низкие вероятности и переоценивают слишком высокие вероятности. Зная об этих тенденциях, следует стремиться их компенсировать, применяя соответствующие гарантированные оценки.

— Не всегда справедливо предположение о том, что все состояния и события независимы. Для событий, имеющих общую причину с высокой вероятностью появления, общая вероятность выше, чем произведение составляющих вероятностей.

— Обычно люди оценивают вероятности сценариев, включающих опасность для имущества, и недооценивают или игнорируют распространенные сценарии, такие как возникновение пожара от электрозамыкания или нагревательного оборудования. Это является причиной использования усеченных данных об инцидентах возникновения пожара при оценке вероятностей возгорания.

— Обычно инженеры используют данные о тщательном исследовании пожара в каждом инциденте. Это может привести к некоторым заблуждениям при оценке вероятностей, так как базы данных включают только необходимую часть информации о происшедших пожарах, в которой преобладают данные о пожарах с высоким уровнем потерь и со смертельным исходом. Таким образом, могут быть пропущены менее опасные пожары, где фактически происходит большинство смертельных случаев, а также наиболее крупные пожары, наносящие большой ущерб имуществу.

— Неблагоразумно считать нулевой вероятность сценариев, которые никогда не были документально описаны в доступных базах данных по ущербу от пожара. Если подобное упущение отражает недостаток данных, то хорошей практикой может быть использование более высокой вероятности для общего сценария, который включает более точные данные для оценки вероятности. Также возможно использование статистических методов оценки вероятности события, которое еще не произошло.

Величина риска чаще всего складывается из двух величин: вероятности и возможного ущерба.

В качестве количественной оценки вероятности на основе данных обычно используют частоту, которую вычисляют путем деления предполагаемого количества исследуемых событий на период или количество возможностей появления событий. Знаменатель может измеряться в единицах времени (например, количество событий в год), количестве человек (например, количество пожаров на тысячу человек), единицах стоимости имущества (например, количество пожаров на общую стоимость всех зданий и их содержимого), количестве зданий (например, пожары на тысячу зданий данного типа) или других единицах (например, пожары на тысячу компаний, владеющих или использующих производственные здания одного типа).

Базы данных для числителей или знаменателей могут быть созданы на основе выборочных данных (допускающих статистическую выборку данных для оценки размера полной группы или генеральной совокупности, из которой отобрана выборка) или путем сбора сведений (обеспечивающего наиболее полные данные о группе).

Главное преимущество использования моделирования состоит в том, что, в отличие от других методов оценки, оно обычно обеспечивает получение не только количественных оценок, необходимых для анализа риска объекта защиты, но также помогает понять взаимосвязь изменений в объекте защиты с изменениями полученных значений вероятности. Эта взаимосвязь необходима в случае, когда при оценке пожарного риска первоначального состояния объекта защиты не получена приемлемая оценка соответствующего риска.

Использование модели не исключает использование экспериментальных или экспертных данных, но уменьшает потребность в данных по другим переменным.

Оценка вероятности может быть проведена на основе технического или научного анализа.

4.2 . Оценка ущербов.

4.2.1 Основные принципы системного анализа и моделирования процесса причинения ущерба.

Существует два основных подхода к оценке ущерба в результате реализации риска природных и природно-техногенных процессов.

Первый подход основан на подсчете возможного ущерба от реализации конкретного опасного процесса. Здесь широко используются такие показатели, как общее число жертв, общее число пострадавших, общий объем экономических потерь и т.д.

При втором подходе риск оценивается по тем средствам, которые необходимо вложить в восстановление инфраструктуры территории, человеческого и экологического потенциала после реализации риска.

Если отсутствует точная информации о времени и возможности наступления аварийной ситуации, но необходимо принять решение о дальнейшем ведении деятельности, либо о ее приостановке, изменении интенсивности или применении дополнительных мер защиты. Ситуация, связанная с вероятностным прогнозом описывается с помощью так называемой «платежной матрицы» (табл. 4.4).

Источник