Тест решение квадратных неравенств графическим способом

Тест по теме: «решение квадратичных неравенств графическим способом»
тест по алгебре (9 класс) по теме

Тест предназначен для учащихся 9 классов. Выполняется на компьтере. Также предусмотрен текстовый вариант.

Скачать:

Вложение	Размер
test_po_teme_reshenie_neravenstv_graficheskim_metdom.doc	53 КБ

Предварительный просмотр:

Тест по теме: «Решение неравенств графическим методом».

1. Графиком квадратичной функции является

2. Графиком функции у=ах 2 +вх +с является парабола, ветви которой направлены вниз, если

не имеет корней

всё множество решений

4. Если при решении неравенства второй степени ах 2 +вх +с>0 получаем, что Д 0, то

всё множество действительных чисел

одно число – корень уравнения

5. Если при решении неравенства второй степени ах 2 +вх +с≥0 получаем, что Д=0 и а

всё множество действительных чисел

одно число – корень уравнения

6. Если при решении неравенства второй степени ах 2 +вх +с 0, то

всё множество действительных чисел

одно число – корень уравнения

7. Если квадратный трёхчлен не имеет корней, то график соответствующей функции расположен

пересекает ось ОХ

1. Если при решении неравенства второй степени ах 2 +вх +с 0), решая уравнение ах 2 +вх +с=0 мы получаем, что Д

9. Если при решении неравенства второй степени ах 2 +вх +с>0 получаем, что Д>0 и а>0, то имеет вид:

10. Я понял данную тему на оценку

По теме: методические разработки, презентации и конспекты

Разработка урока по теме «Решение уравнений и неравенств с модулем»

Целью урока является совершенствование навыков решения уравнений и неравенств с модулем. В ходе урока рассматриваются рациональные приёмы и методы решения. Урок предназначен для классов с .

Урок по теме «Решение уравнений и неравенств с параметром»

9-й класс. Урок по теме «Решение уравнений и неравенств с параметром»Чехолкова Алла ВладимировнаЦель: Выработка навыка решения уравнений и неравенств с параметром различными способами. Разв.

презентация к уроку решение систем уравнений и неравенств графическим способом

презентация к уроку» решение систем уравнений и неравенств графическим способом».

тест по теме «Решение квадратного неравенства»

Тест проверяет умение находить множество решений квадратного неравенства с одной переменной, опираясь на графические изображения. Задания базового уровня. 4 варианта.

Тест по темам « Решение уравнений и их систем», «Решение неравенств и их систем» и «Решение уравнений, неравенств, систем неравенств с модулем».

Задания теста соответствуют содержанию учебника «Алгебра. 9 класс : учеб. для учащихся общеобразовательных учреждений / Ю. Н. Макарычев , Н. Г. Миндюк , К. И. Нешков , И. Е. Феоктист.

Коспект урока по теме: «Решение систем уравнений второй степени способом сложения и способом введения новой переменной»

Учебный матeриал в раздел «Основная школа»Конспект урока алгебры в 9 классе с применением проблемно-модульной технологии.

Подготовка к ГИА Тест на тему «Решение линейных неравенств» в 9 классе 2019-2020 учебный год.

1 вариантРешите неравенства: 1. 9-5х Мне нравится

Источник

тест по теме «Решение квадратного неравенства»
тест по алгебре (8 класс) на тему

Тест проверяет умение находить множество решений квадратного неравенства с одной переменной, опираясь на графические изображения. Задания базового уровня. 4 варианта.

Скачать:

Вложение	Размер
test_po_teme_reshenie_kvadratnyh_neravenstv.rar	226.86 КБ

Предварительный просмотр:

Тест по теме «Решение квадратных неравенств»

По теме: методические разработки, презентации и конспекты

Тест «Квадратные неравенства»

Тест содержит два варианта.

Тема 6. АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА. КВАДРАТНЫЕ НЕРАВЕНСТВА. РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА ВЫСШИХ СТЕПЕНЕЙ. ДРОБНО-РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА.Теория. Ключевые методы решения задач. Упражнения.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .

Итоговый контроль по темам № 6,7: «Алгебраические неравенства. Квадратные неравенства. Рациональные неравенства высших степеней. Дробно-рациональные неравенства. Неравенства с модулем. Иррациональные неравенства»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, .

Тест по теме «Системы квадратных неравенств. Алгебра 9 класс»

Система квадратных неравенств- основная тема 9 класса,знание которой поможет дальнейшему изучению решений логарифмических и показательных неравенств .

Тематическое планирование по теме «Квадратное неравенство» + тесты

Тематическое планирование по теме «Квадратное неравенство» + тесты.

Тест на соответствие по теме «Квадратные неравенства»

Тест содержит два варианта заданий, к которым предложены ответы для установления соответствия.

Конспект урока по алгебре в 9 классе. Тема: Решение квадратных неравенств. Задания, сводящиеся к решению квадратных неравенств

1. Образовательная: формирование навыков решения квадратных неравенств на основе свойств квадратичной функции.

Источник

Тест по теме «Квадратные неравенства»

Выбранный для просмотра документ Цыгер О.В. тест для 9 класса Квадратные неравенства.docx

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 87»

г. Северск, Томской области

Методическая разработка урока

для учащихся 9 классов

Цыгер Ольга Викторовна

1. Цыгер Ольга Викторовна.

2. МБОУ «СОШ № 87», г. Северск, Томской области, учитель математики.

3. Предмет: математика.

4. Тип урока: тест.

5. комплектация работы: данный файл.

Данный тест составлен по теме «Квадратные неравенства» и предназначен для учащихся 9 классов. Он может быть использован на уроках промежуточного и обобщающего контроля по данной теме, и при подготовке к ГИА.

Данный тест позволяет систематизировать знания учащихся по теме «Квадратные неравенства», своевременно выявить пробелы в изученном материале. Принцип построения теста — «от простого к сложному» — позволяет использовать его в классах с разной математической подготовкой. Используемые здесь задания построены таким образом, чтобы учащиеся смогли оценить как существенные, так и несущественны для данной задачи свойства квадратичной функции. Отрабатываются два способа решения неравенств второй степени: аналитический и графический. В тесте представлены все типы квадратных неравенств имеющие два корня, один или ни одного. Также представлены задания более сложные, которые сводятся к решению неравенств второй степени и требуют нестандартного подхода.

Источник

Тест решение квадратных неравенств графическим способом

На каком рисунке изображено множество решений неравенства

В ответе укажите номер правильного варианта.

Решим неравенство: &nbsp Корнями уравнения являются числа 1 и 3. Поэтому

Множество решений неравенства изображено на рис. 1.

Правильный ответ указан под номером 1.

Решение какого из данных неравенств изображено на рисунке?

В ответе укажите номер правильного варианта.

1)

2)

3)

4)

Решим каждое из неравенств.

1) &nbsp — решений нет.

2) &nbsp

3) &nbsp верно для всех

4) &nbsp

На рисунке изображено решение четвёртого неравенства.

Источник

Решение квадратных неравенств с помощью графика

Квадратным неравенством называют неравенство вида \(ax^2 + bx + c> 0\) , где (вместо знака > может быть, разумеется, любой другой знак неравенства).

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения \(ax^2+bx+c=0\) . Для этого необходимо найти дискриминант данного квадратного уравнения. Можно получить 3 случая:

1) D = 0, квадратное уравнение имеет один корень;

2) D > 0, квадратное уравнение имеет два корня;

3) D \(a\) возможно одно из шести расположений графика функции \(y=ax^2+bx+c\) :

Если требуется найти числовой промежуток, на котором квадратный трехчлен \(ax^2+bx+c\) больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если требуется найти числовой промежуток, на котором квадратный трехчлен \(ax^2+bx+c\) меньше нуля, то этот числовой промежуток расположен там, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое – не входят.

Такой метод решения квадратного неравенства называется графическим.

Пример 1. Решить \(x^2–15x+50 > 0\) .

Решаем квадратное уравнение \(x^2–15x+50=0\) .

\(D = b^2–4ac = (–15)2–4\cdot1\cdot50 = 225–200 = 25\) .

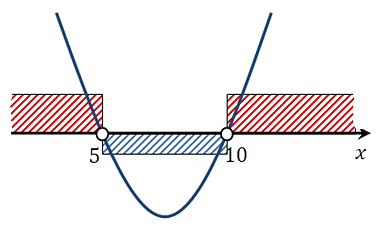
Строим ось OX. Отметим полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х 2 положительный:

Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать. Записываем ответ: \(x\in(-\infty; 5)\cup(10; +\infty)\) .

*Знак U обозначает объединение решений. Образно можно выразиться так: решением является «этот» и « еще этот» интервал.

Пример 2. Решить: \(–x^2+x+20 ≤ 0\) .

Решаем квадратное уравнение \(–x^2+x+20=0\) .

\(D = b^2–4ac = 12–4\cdot(–1)\cdot20 = 1+80 = 81\) .

Строим ось OX. Отметим полученные корни. Так как неравенство у нас нестрогое, то заштрихуем обозначения корней. Схематично строим параболу, расположена она ветвями вниз, так как коэффициент при х 2 отрицательный (он равен –1):

Определяем визуально положительные и отрицательные области. Сопоставляем с исходным неравенством (знак у нас ≤ 0). Неравенство будет верно при х ≤ – 4 и х ≥ 5. Записываем ответ: \(x\in(-\infty;-4]\cup[5;+\infty)\) .

*Указаны квадратные скобки – это обозначает, что границы интервала входят в решение. Ось OY мы на эскизах не указали, так как она в данной ситуации не играет никакой роли, то есть при построении эскиза ось OY строить необязательно.

По графику функции \(y=x^2-4x+3\) определите промежутки, на которых функция принимает отрицательные значения.

Источник