Основы теории теплообмена
Теория теплообмена, основные понятия и определения. Теплопроводность. Предмет и методы теории теплообмена. Основные виды переноса теплоты. Понятия теплоотдачи и теплопередачи. Температурное поле, температурный градиент. Закон Фурье. Расчетные формулы стационарной теплопроводности для плоской и цилиндрической стенок при граничных условиях 1 и 3 рода (теплопередача).
Основы теории теплообмена
Теплопередача — это процесс переноса теплоты от одного теплоносителя к другому через разделяющую стенку. Теплопередача связана с весьма сложными процессами и при ее изучении необходимо знать законы теории теплообмена и методы анализа, применяемые в физике, термодинамике, гидродинамике и химии.
Сложный процесс переноса теплоты разбивают на ряд более простых. Такой прием упрощает его изучение. Кроме того, каждый простой процесс переноса теплоты подчиняется своим законам. Существует три простейших способа передачи теплоты: теплопроводность, конвекция, излучение.
Явление теплопроводности состоит в переносе теплоты микрочастицами (молекулами, атомами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур.
Конвективный теплоперенос (конвекция) наблюдается лишь в жидкостях и газах. Конвекция — это перенос теплоты вместе с макроскопическими объемами вещества. Следует иметь в виду, что одновременно с конвекцией всегда существует и теплопроводность. Однако конвекция обычно является определяющей, т. к. она интенсивнее теплопроводности.
Конвекцией можно передавать теплоту на очень большие расстояния (например, при движении газа по трубам). Движущаяся среда (жидкость или газ), используемая для переноса теплоты, называется теплоносителем.
Третьим способом переноса теплоты является излучение. За счет излучения теплота передается во всех лучепрозрачных средах, в том числе и в вакууме. Носителями энергии при теплообмене излучением являются фотоны, излучаемые и поглощаемые телами, участвующими в теплообмене.
В большинстве случаев перенос тепла осуществляется несколькими способами одновременно. Например, конвективная теплопередача от газа к стенке практически всегда сопровождается параллельным переносом теплоты излучением.
Основные понятия и определения
Интенсивность переноса теплоты характеризуется плотностью теплового потока. Плотность теплового потока — это количество теплоты, передаваемое в единицу времени через единичную плотность поверхности, q [Вт/м2].
Мощность теплового потока или просто тепловой поток — это количество теплоты, передаваемое в единицу времени через произвольную поверхность F, [Вт].
поверхность теплообмена F — это поверхность, через которую происходит передача тепла. Например, при остывании теплоносителя в трубе диаметром d и длиной l, тепло передается от горячего теплоносителя к окружающей среде через цилиндрическую поверхность трубы. В этом случае 
Перенос теплоты зависит от распределения температуры по объему тела или пространства. Температурным полем называется совокупность мгновенных значений температуры во всех точках тела или системы тел в данный момент времени. Математическое описание температурного поля имеет вид:
где t — температура;
x, y,z — пространственные координаты;

Температурное поле, описываемое приведенным уравнением, называется нестационарным. В этом случае температуры зависят от времени.
В том случае, когда распределение температуры в теле не изменяется со временем, температурное поле называется стационарным
если температура изменяется только по одной или двум пространственным координатам, то температурное поле называется соответственно одно— и двухмерным:
Температурные поля (1.2) и (1.3) называются трехмерными.
Поверхность, во всех точках которой температура одинакова, называется изотермической. Изотермические поверхности могут быть замкнутыми, но не могут пересекаться. Быстрее всего температура изменяется при движении в направлении, перпендикулярном изотермической поверхности. Скорость изменения температуры по нормали к изотермической поверхности характеризуется градиентом температуры.

(grad t) — есть вектор, направленный по нормали к изотермической поверхности и численно равный производной пот температуры по этому направлению:

Рисунок 1 — Расположение градиента температуры и вектора теплового потока относительно изотермы t2=Const температурного поля
где 
Теория теплопроводности рассматривает тело как непрерывную среду. Согласно основному закону теплопроводности — закону Фурье — вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален вектору градиента температуры:

где 
Знак «-» указывает на противоположное направление вектора теплового потока и вектора градиента температуры. Вектор плотности теплового потока q всегда направлен в сторону наибольшего уменьшения температуры.
скалярная величина вектора плотности теплового потока:

Из формулы следует, что коэффициент теплопроводности 
Коэффициент теплопроводности является физическим параметром и зависит от химической природы вещества и его физического состояния (плотности, влажности, давления, температуры). Диапазоны изменения 
 |
Рисунок 2 — Теплопроводность при стационарном режиме
Однослойная плоская стенка



Рисунок 3 — Изменение температур по толщине однородной плоской стенки

где 

Распределение температур в плоской однородной стенке — линейное.
В большинстве практических задач приближенно предполагается, что коэффициент теплопроводности 


Тепловой поток (мощность теплового потока) определяется по формуле:

Многослойная плоская стенка


| |


| |


| |


| |
Рассмотрим для тех же условий многослойную плоскую стенку с толщиной слоев d1, d2,…, dn с соответствующими коэффициентами теплопроводности l1, l2,…, ln (рисунок 4). Здесь слои плотно прилегают друг к другу.
В этом случае плотность теплового потока определяется по формуле:
Рисунок 4 — Распределение температур по толщине многослойной плоской стенки

где n — число слоев многослойной стенки;
tc1 и tc(n+1) — температуры на внешних границах многослойной стенки;

Плотность теплового потока, проходящего через все слои, в стационарном режиме одинакова. А так как коэффициент теплопроводности l различен, то для плоской многослойной стенки распределение температур — ломаная линия.
Рассчитав тепловой поток через многослойную стенку, можно найти температуру на границе любого слоя. Для к-го слоя можно записать:

Однородная цилиндрическая стенка
Задача о распространении тепла в цилиндрической стенке также одномерная, если ее рассматривать в цилиндрических координатах. температура изменяется только вдоль радиуса r, а по длине и по ее периметру остается неизменной.
В соответствии с законом Фурье, тепловой поток через однородную цилиндрическую стенку длиной l определяется по формуле:

Тепловой поток Q через цилиндрическую стенку можно отнести к единице длины l:

где ql — линейная плотность теплового потока, Вт/м;

 | ||||||||
В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и различают поэтому средний по поверхности коэффициент теплоотдачи и локальный или местный коэффициент теплоотдачи, соответствующий единичному элементу поверхности. Процессы теплоотдачи неразрывно связаны с условиями движения жидкости. Как известно из курса гидравлики, имеются два основных режима течения: ламинарный и турбулентный. При ламинарном режиме течение имеет спокойный, струйчатый характер. При турбулентном — движение неупорядоченное, вихревое. Изменение режима движения происходит при некоторой «критической» скорости, которая в каждом конкретном случае различна. В результате специальных исследований О. Рейнольдс в 1883 г. установил, что в общем случае режим течения жидкости определяется не только одной скоростью, а особым безразмерным комплексом, состоящим из скорости движения жидкости w, коэффициента кинематической вязкости жидкости v и характерного размера l канала или обтекаемого тела. Теперь такой комплекс называется критерием или числом Рейнольдса и обозначается символом Re = wl/v. Как известно из гидродинамики, критерий Рейнольдса, называемый иначе критерием кинематического подобия, характеризует соотношение между инерционными силами и силами трения и является основной характеристикой, определяющей режим течения жидкости. Переход ламинарного режима в турбулентный происходит при критическом значении этого критерия Reкр. Например, при движении жидкости в трубах Reкр=wкpd/v=2·10 3 . При турбулентном движении весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и исчезают. В точности механизм вихреобразования еще не установлен. Одной из причин их возникновения является потеря устойчивости ламинарного течения, сопровождающаяся образованием завихрений, которые затем диффундируют в ядро и, развиваясь, заполняют весь поток. Одновременно с этим вследствие вязкости жидкости эти вихри постепенно затухают и исчезают. Благодаря непрерывному образованию вихрей и их диффузии происходит сильное перемешивание жидкости, называемое турбулентным смешением. Чем больше вихрей, тем интенсивнее перемешивание жидкости и тем больше турбулентность потока. Различают естественную и искусственную турбулентность. Первая устанавливается естественно. Для случая стабилизированного движения внутри гладкой трубы турбулентность вполне определяется значением критерия Re. Вторая вызывается искусственным путем вследствие наличия в потоке каких-либо преград, турбулизирующих решеток и других возмущающих источников. Однако при любом виде турбулентности в тонком слое у поверхности из-за наличия вязкого трения течение жидкости затормаживается и скорость падает до нуля. Этот слой принято называть пограничным или вязким подслоем.
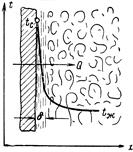
Теория пограничного слоя была разработана Л. Прандтлем в начале прошлого столетия (1904 г.) Рис. 4-1. Характер изменения температуры в пограничном слое при нагревании жидкости. Для процессов теплоотдачи режим движения рабочей жидкости имеет очень большое значение, так как им определяется механизм переноса тепла. При ламинарном режиме перенос тепла в направление нормали к стенке в основном осуществляется путем теплопроводности. При турбулентном режиме такой способ переноса тепла сохраняется лишь в вязком подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемешивания частиц жидкости. В этих условиях для газов и обычных жидкостей интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя, которое по сравнению с термическим сопротивлением ядра оказывается определяющим. В этом легко убедиться, если проследить за изменением температуры жидкости в направлении нормали к стенке (рис. 4.1). Как видно, наибольшее изменение температуры происходит в пределах тонкого слоя у поверхности, через который тепло передается путем теплопроводности. Следовательно, как для ламинарного, так и для турбулентного режима течения вблизи самой поверхности применим закон Фурье:
q = -λ grad t, где grad t — градиент температуры в слоях жидкости, прилегающих к поверхности твердого тела, °С/м. Процесс теплоотдачи является сложным процессом, а коэффициент теплоотдачи является сложной функцией различных величин, характеризующих этот процесс. В общем случае коэффициент теплоотдачи является функцией формы Ф, размеров l1, l2, . температуры поверхности нагрева tс, скорости жидкости w, ее температуры tж, физических свойств жидкости — коэффициента теплопроводности λ, теплоемкости ср, плотности ρ, вязкости μ и других факторов: В качестве теплоносителей в настоящее время применяются самые разнообразные вещества — воздух, газы, вода, масла, бензол, нефть, бензин, спирты, расплавленные металлы и различные специальные смеси. В зависимости от рода и физических свойств этих веществ теплоотдача протекает различно и своеобразно. Для каждого теплоносителя физические свойства имеют определенные значения и, как правило, являются функцией температуры, а некоторые из них и давления. Коэффициент теплопроводности λ характеризует способность вещества проводить тепло; его значение определяет количество тепла, которое проходит в единицу времени через 1 м 2 сечения при изменении температуры в один градус на 1 м пути теплового потока (см. разд. 2). Удельная теплоемкость с определяет количество тепла, необходимое для нагревания 1 кг вещества на один градус. При постоянном давлении теплоемкость обозначается cр (изобарная теплоемкость), а при постоянном объеме cv (изохорная теплоемкость). Плотность вещества ρ = m/V представляет собой массу вещества в единице объема. Коэффициент температуропроводности а=λ/сρ характеризует скорость изменения температуры в теле (см. разд. 2). Вязкость. Все реальные жидкости обладают вязкостью; между частицами или слоями, движущимися с различными скоростями, всегда возникает сила внутреннего трения, противодействующая движению. Согласно закону вязкого трения Ньютона эта сила, отнесенная к единице поверхности, пропорциональна изменению скорости в направлении нормали к этой поверхности:
Величина μ называется коэффициентом вязкости или коэффициентом динамической вязкости. При dw/dn=1 S = μ, следовательно, коэффициент вязкости выражает собой силу трения, приходящуюся на единицу поверхности соприкосновения двух жидких слоев, «скользящих» друг по другу при условии, что на единицу длины нормали к поверхности скорость движения изменяется на единицу. В уравнения гидродинамики и теплопередачи часто входит отношение коэффициента вязкости к плотности, называемое коэффициентом кинематической вязкости: Температурный коэффициент объемного расширения
где υ — удельный объем, м 3 /кг. Для газов температурный коэффициент объемного расширения определяется по формуле Механизм и интенсивность переноса теплоты зависят от характера движения жидкости в пограничном слое. Если движение внутри теплового пограничного слоя ламинарное, то теплота в направлении, перпендикулярном к стенке, переносится теплопроводностью. Однако у внешней границы слоя, где температура по нормали к стенке меняется незначительно, преобладает перенос теплоты конвекцией вдоль стенки. При турбулентном течении в тепловом пограничном слое перенос теплоты в направлении к стенке в основном обусловлен турбулентным перемешиванием жидкости. Интенсивность такого переноса теплоты существенно выше интенсивности переноса теплоты теплопроводностью. Однако непосредственно у стенки, в ламинарном подслое, перенос теплоты к стенке осуществляется обычной теплопроводностью. Изменение физических свойств жидкости в пограничном слое зависит от температуры, в связи с чем интенсивность теплообмена между жидкостью и стенкой оказывается различной в условиях нагревания и охлаждения жидкости. Так, например, для капельных жидкостей интенсивность теплообмена при нагревании будет большей, чем при охлаждении, вследствие уменьшения пограничного слоя. Следовательно, теплоотдача зависит от направления теплового потока. Очень большое значение для теплообмена имеют форма и размер поверхностей; в зависимости от них может резко меняться характер движения жидкости и толщина пограничного слоя. Источник |
























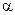 , который определяется по формуле Ньютона
, который определяется по формуле Ньютона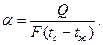

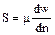 .
.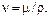
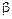 характеризует относительное изменение объема при изменении температуры на один градус:
характеризует относительное изменение объема при изменении температуры на один градус: