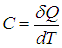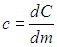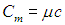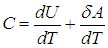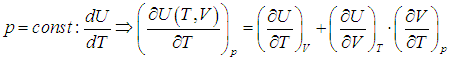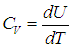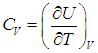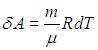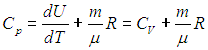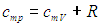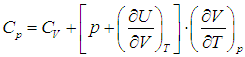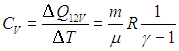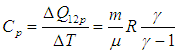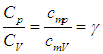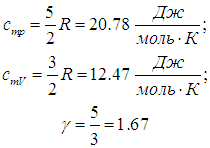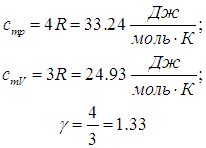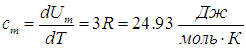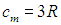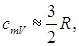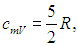Теплоемкость способы ее расчета

Формула для расчёта удельной теплоёмкости вещества

Удельная теплоёмкость — это энергия, которая требуется для увеличения температуры 1 грамма чистого вещества на 1°. Параметр зависит от его химического состава и агрегатного состояния: газообразное, жидкое или твёрдое тело. После его открытия начался новый виток развития термодинамики, науки о переходных процессах энергии, которые касаются теплоты и функционирования системы.

Как правило, удельная теплоёмкость и основы термодинамики используются при изготовлении радиаторов и систем, предназначенных для охлаждения автомобилей, а также в химии, ядерной инженерии и аэродинамике. Если вы хотите узнать, как рассчитывается удельная теплоёмкость, то ознакомьтесь с предложенной статьёй.

Формула

Перед тем, как приступить к непосредственному расчёту параметра следует ознакомиться с формулой и её компонентами.

Формула для расчёта удельной теплоёмкости имеет следующий вид:

Знание величин и их символических обозначений, использующихся при расчёте, крайне важно. Однако необходимо не только знать их визуальный вид, но и чётко представлять значение каждого из них. Расчёт удельной теплоёмкости вещества представлен следующими компонентами:

ΔT – символ, означающий постепенное изменение температуры вещества. Символ «Δ» произносится как дельта.

ΔT можно рассчитать по формуле:

• t1 – первичная температура;
• t2 – конечная температура после изменения.

m – масса вещества используемого при нагреве (гр).

Q – количество теплоты (Дж/J)

На основании Цр можно вывести и другие уравнения:

• Q = m*цp*ΔT – количество теплоты ;
• m = Q/цр*(t2 — t1) – массы вещества;
• t1 = t2–(Q/цp*m) – первичной температуры;
• t2 = t1+(Q/цp*m) – конечной температуры.

Инструкция по расчёту параметра

Рассчитать с вещества достаточно просто и чтобы это сделать нужно, выполнить следующие шаги:

1. Взять расчётную формулу: Теплоемкость = Q/(m*∆T)
2. Выписать исходные данные.
3. Подставить их в формулу.
4. Провести расчёт и получим результат.

В качестве примера произведём расчёт неизвестного вещества массой 480 грамм обладающего температурой 15ºC, которая в результате нагрева (подвода 35 тыс. Дж) увеличилась до 250º.

Согласно инструкции приведённой выше производим следующие действия:

Выписываем исходные данные:

• Q = 35 тыс. Дж;
• m = 480 г;
• ΔT = t2–t1 =250–15 = 235 ºC.

Берём формулу, подставляем значения и решаем:

с=Q/(m*∆T)=35тыс.Дж/(480 г*235º)=35тыс.Дж/(112800 г*º)=0,31 Дж/г*º.

Расчёт

Выполним расчёт C_P воды и олова при следующих условиях:

• m = 500 грамм;
• t1 =24ºC и t2 = 80ºC – для воды;
• t1 =20ºC и t2 =180ºC – для олова;
• Q = 28 тыс. Дж.

Для начала определяем ΔT для воды и олова соответственно:

• ΔТв = t2–t1 = 80–24 = 56ºC
• ΔТо = t2–t1 = 180–20 =160ºC

Затем находим удельную теплоёмкость:

1. с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
2. с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.

Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.

Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.

Как рассчитать теплоемкость продуктов питания

При расчёте емкости питания уравнение примет следующий вид:

• w – количество воды в продукте;
• p – количество белков в продукте;
• f – процентное содержание жиров;
• c – процентное содержание углеводов;
• a – процентное содержание неорганических компонентов.

Определим теплоемкость плавленого сливочного сыра Viola. Для этого выписываем нужные значения из состава продукта (масса 140 грамм):

• вода – 35 г;
• белки – 12,9 г;
• жиры – 25,8 г;
• углеводы – 6,96 г;
• неорганические компоненты – 21 г.

Затем находим с:

• с=(4.180*w)+(1.711*p)+(1.928*f)+(1.547*c)+(0.908*a)=(4.180*35)+(1.711*12,9)+(1.928*25,8) + (1.547*6,96)+(0.908*21)=146,3+22,1+49,7+10,8+19,1=248 кДж /кг*ºC.

Полезные советы

Всегда помните, что:

• процесс нагревания металла проходит быстрее, чем у воды, так как он обладает C_P в 2,5 раза меньше;
• по возможности преобразуйте полученные результаты в более высокий порядок, если позволяют условия;
• в целях проверки результатов можно воспользоваться интернетом и посмотреть с для расчётного вещества;
• при равных экспериментальных условиях более значительные температурные изменения будут наблюдаться у материалов с низкой удельной теплоёмкостью.

Видео

Разобраться в этой теме вам поможет видео урок.

Источник

Удельная теплоемкость вещества

О чем эта статья:

Нагревание и охлаждение

Эти два процесса знакомы каждому. Вот нам захотелось чайку, и мы ставим чайник, чтобы нагреть воду. Или ставим газировку в холодильник, чтобы охладить.

Логично предположить, что нагревание — это увеличение температуры, а охлаждение — ее уменьшение. Все, процесс понятен, едем дальше.

Но не тут-то было: температура меняется не «с потолка». Все завязано на таком понятии, как количество теплоты. При нагревании тело получает количество теплоты, а при нагревании — отдает.

• Количество теплоты — энергия, которую получает или теряет тело при теплопередаче.

В процессах нагревания и охлаждения формулы для количества теплоты выглядят так:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует и изменение температуры, о котором мы сказали выше, и удельная теплоемкость, речь о которой пойдет дальше.

А вот теперь поговорим о видах теплопередачи.

Виды теплопередачи

• Теплопередача — это физический процесс передачи тепловой энергии от более нагретого тела к менее нагретому.

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества

c — удельная теплоемкость вещества [Дж/кг*˚C]

C — теплоемкость вещества [Дж/˚C]

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Таблица удельных теплоемкостей

Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.

Источник

2.3. Теплоемкость системы

Введем теперь очень важную термодинамическую характеристику, называемую теплоемкостью системы (традиционно обозначается буквой С с различными индексами).

Теплоемкость системы — это физическая величина, равная количеству теплоты, которое необходимо передать системе, чтобы увеличить ее температуру на один кельвин (градус):

Теплоемкость — величина аддитивная, она зависит от количества вещества в системе. Поэтому вводят также удельную теплоемкость

Удельная теплоемкость — это теплоемкость единицы массы вещества

и молярную теплоемкость

Молярная теплоемкость — это теплоемкость одного моля вещества

Поскольку количество теплоты не есть функция состояния и зависит от процесса, теплоемкость также будет зависеть от способа подвода тепла к системе. Чтобы понять это, вспомним первое начало термодинамики. Разделив равенство ( 2.4 ) на элементарное приращение абсолютной температуры dT, получим соотношение

Второе слагаемое, как мы убедились, зависит от вида процесса. Отметим, что в общем случае неидеальной системы, взаимодействием частиц которой (молекул, атомов, ионов и т. п.) пренебречь нельзя (см., например, § 2.5 ниже, в котором рассматривается ван–дер–ваальсовский газ), внутренняя энергия зависит не только от температуры, но и от объема системы. Это объясняется тем, что энергия взаимодействия зависит от расстояния между взаимодействующими частицами. При изменении объема системы меняется концентрация частиц, соответственно, меняется среднее расстояние между ними и, как следствие, меняется энергия взаимодействия и вся внутренняя энергия системы. Другими словами, в общем случае неидеальной системы

.

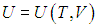
Поэтому, в общем случае первое слагаемое нельзя писать в виде полной производной, полную производную необходимо заменить на частную производную с дополнительным указанием на то, при какой постоянной величине она вычисляется. Например, для изохорного процесса:

.

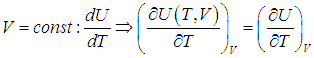
Или для изобарного процесса

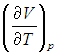
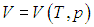
Входящая в это выражение частная производная вычисляется с помощью уравнения состояния системы, записанного в виде . Например, в частном случае идеального газа

,

эта производная равна

.

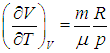
Мы рассмотрим два частных случая, соответствующих процессу подведения теплоты:

• постоянном объеме;
• постоянном давлении в системе.

В первом случае работа dА = 0 и мы получаем теплоемкость С_V идеального газа при постоянном объеме:

С учетом сделанной выше оговорки, для неидеальной системы соотношение (2.19) необходимо записать в следующем общем виде

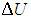
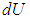
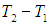
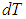
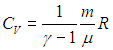
Заменив в 2.7 на , а на немедленно получаем:

.

Для вычисления теплоемкости идеального газа С_p при постоянном давлении (dp = 0) мы учтем, что из уравнения ( 2.8 ) следует выражение для элементарной работы при бесконечно малом изменении температуры

Получаем в итоге

Разделив это уравнение на число молей вещества в системе, получаем аналогичное соотношение для молярных теплоемкостей при постоянном объеме и давлении, называемое соотношением Майера

Приведем для справки общую формулу — для произвольной системы — связывающую изохорную и изобарную теплоемкости:

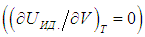
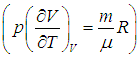
Выражения (2.20) и (2.21) получаются из этой формулы путем подстановки в неё выражения для внутренней энергии идеального газа и использования его уравнения состояния (см. выше):

.

Теплоемкость данной массы вещества при постоянном давлении больше теплоемкости при постоянном объеме, так как часть подведенной энергии тратится на совершение работы и для такого же нагревания требуется подвести больше теплоты. Отметим, что из (2.21) следует физический смысл газовой постоянной:

Газовая постоянная R — это работа, совершаемая молем идеального газа при повышении его температуры на 1 К при постоянном давлении.

Таким образом, теплоемкость оказывается зависящей не только от рода вещества, но и от условий, в которых происходит процесс изменения температуры.

Как мы видим, изохорная и изобарная теплоемкости идеального газа от температуры газа не зависят, для реальных веществ эти теплоемкости зависят, вообще говоря, также и от самой температуры Т.

Изохорную и изобарную теплоемкости идеального газа можно получить и непосредственно из общего определения, если воспользоваться полученными выше формулами ( 2.7 ) и ( 2.10 ) для количества теплоты, получаемого идеальным газом при указанных процессах.

Для изохорного процесса выражение для С_V следует из ( 2.7 ):

Для изобарного процесса выражение для С_р вытекает из ( 2.10 ):

Для молярных теплоемкостей отсюда получаются следующие выражения

Отношение теплоемкостей равно показателю адиабаты:

На термодинамическом уровне нельзя предсказать численное значение g; нам удалось это сделать лишь при рассмотрении микроскопических свойств системы (см. выражение ( 1.19 ), а также ( 1.28 ) для смеси газов). Из формул ( 1.19 ) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.

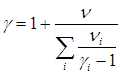
Одноатомные газы (i = 3):

Двухатомные газы (i = 5):

Многоатомные газы (i = 6):

Экспериментальные данные для различных веществ приведены в таблице 1.

Таблица 1

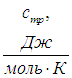
Видно, что простая модель идеальных газов в целом неплохо описывает свойства реальных газов. Обращаем внимание, что совпадение было получено без учета колебательных степеней свободы молекул газа.

Мы привели также значения молярной теплоемкости некоторых металлов при комнатной температуре. Если представить кристаллическую решетку металла как упорядоченный набор твердых шариков, соединенных пружинками с соседними шариками, то каждая частица может только колебаться в трех направлениях (i_кол = 3), и с каждой такой степенью свободы связаны кинетическая k_ВТ/2 и такая же потенциальная энергия. Поэтому на частицу кристалла приходится внутренняя (колебательная) энергия k_ВТ. Умножая на число Авогадро, получим внутреннюю энергию одного моля

откуда вытекает значение молярной теплоемкости

(Вследствие малого коэффициента теплового расширения твердых тел для них не различают с_р и c_v). Приведенное соотношение для молярной теплоемкости твердых тел называется законом Дюлонга и Пти, и из таблицы видно хорошее совпадение расчетного значения

Говоря о неплохом соответствии приведенных соотношений и данных опытов, следует отметить, что оно наблюдается лишь в определенном диапазоне температур. Иначе говоря, теплоемкость системы зависит от температуры, и формулы (2.24) имеют ограниченную область применения. Рассмотрим сначала рис. 2.10, на котором изображена экспериментальная зависимость теплоемкости с_тV газообразного водорода от абсолютной температуры Т.

Рис. 2.10. Молярная теплоемкость газообразного водорода Н₂ при постоям ном объеме как функция температуры (экспериментальные данные)

Ниже, для краткости, говорится об отсутствии у молекул тех или иных степеней свободы в определенных температурных интервалах. Еще раз напомним, что речь в действительности идет о следующем. По квантовым причинам, относительный вклад во внутреннюю энергию газа отдельных видов движения действительно зависит от температуры и в определенных температурных интервалах может быть мал настолько, что в эксперименте — всегда выполняемом с конечной точностью — он незаметен. Результат эксперимента выглядит так, как будто этих видов движения нет, нет и соответствующих степеней свободы. Число и характер степеней свободы определяются структурой молекулы и трехмерностью нашего пространства — от температуры они зависеть не могут.

Вклад во внутреннюю энергию от температуры зависит и может быть мал.

При температурах ниже 100 К теплоемкость

что указывает на отсутствие у молекулы как вращательных, так и колебательных степеней свободы. Далее с ростом температуры теплоемкость быстро возрастает до классического значения

характерного для двухатомной молекулы с жесткой связью, в которой нет колебательных степеней свободы. При температурах свыше 2 000 К теплоемкость обнаруживает новый скачок до значения

Этот результат свидетельствует о появлении еще и колебательных степеней свободы. Но все это пока выглядит необъяснимым. Почему молекула не может вращаться при низких температурах? И почему колебания в молекуле возникают лишь при очень высоких температурах? В предыдущей главе дано краткое качественное рассмотрение квантовых причин подобного поведения. А сейчас можно лишь повторить, что все дело сводится к специфически квантовым явлениям, не объяснимым с позиций классической физики. Эти явления подробно рассмотрены в последующих разделах курса.

http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 236 — таблица характеристических температур «включения» колебательных и вращательных степеней свободы молекул для некоторых конкретных газов;

Обратимся теперь к рис. 2.11, представляющему зависимость молярных теплоемкостей трех химических элементов (кристаллов) от температуры. При высоких температурах все три кривые стремятся к одному и тому же значению

соответствующему закону Дюлонга и Пти. Свинец (Рb) и железо (Fe) практически имеют это предельное значение теплоемкости уже при комнатной температуре.

Рис. 2.11. Зависимость молярной теплоемкости для трех химических элементов — кристаллов свинца, железа и углерода (алмаза) — от температуры

Для алмаза же (С) такая температура еще не достаточно высока. А при низких температурах все три кривые демонстрируют значительное отклонение от закона Дюлонга и Пти. Это еще одно проявление квантовых свойств материи. Классическая физика оказывается бессильной объяснить многие наблюдаемые при низких температурах закономерности.

Источник