Теоретический способ построения модели

Теоретический метод построения модели.

Основы моделирования

Моделирование как метод исследования технологических процессов включает в себя следующие основные этапы:

· постановка цели моделирования

· проверка адекватности модели и внесение корректив

· использование ее для исследования свойств и поведения объекта .

Одному и тому же объекту-оригиналу в зависимости от целей моделирования мо­жет соответствовать большое число моде­лей, отражающих разные его стороны .

При использовании теоретического под­хода модель строится на основе соотношений, вытекающих из физических законов; при использовании формального подхода — принципов «черного ящика».

Поэтому первый подход применяют в тех случаях, когда известны законы, которым подчиняются технологические процессы, протекающие в объекте моделирования, второй в случае отсутствия такой информации.

Детерминированные модели, построенные с использованием теоретического подхода, имеют ряд существенных преимуществ:

их можно разрабатывать даже при отсутствии действующего объекта, как это часто бывает проектировании;

они качественно более правильно характеризуют процессы, протекающие в объекте, даже при наличии недостаточно точных в количественном отношении параметров модели;

пригодны для обобщений, связанных с изучением общих свойств объектов определенного класса, и для прогнозирования поведения объекта.

Если априорная информация об объекте моделирования не обладает достаточной полнотой или из-за его значительной сложности невозможно описать в виде модели все выходные воздействия, а влияние ненаблюдаемых переменных на выходные координаты объекта существенно, то принимают стохастическую модель.

Наиболее полное представление о поведении объекта дают динамические модели. Однако их использование приводит к довольно сложным вычислительным задачам, поэтому для объектов, инерционностью которых можно пренебречь по сравнению с временным интервалом, на котором решается задача моделирования, или при сравнительно малом спектре возмущений ограничиваются статическими моделями. Когда можно пре­небречь пространственной неравномер­ностью переменных, используют модели с со­средоточенными переменными, в противном случае — модели с распределенными пере­менными. Последние можно построить толь­ко при использовании теоретико-физическо­го подхода. При этом вычислительная зада­ча еще больше усложняется.

Идентификация модели базируется на ис­пользовании активного или пассивного экспе­риментального метода. При активном экспе­рименте исследователь сам выбирает нужное регулярное воздействие, которое поступает на вход объекта. При этом фиксируется ре­акция объекта на регулярные входные воз­действия. При пассивном эксперименте ис­следователь лишь регистрирует случайные входные воздействия, возникающие при нор­мальной эксплуатации объекта, и реакцию объекта на эти воздействия.

Активные методы требуют меньше вре­мени на наблюдение и обработку результа­тов, чем пассивные, и поэтому их применяют во всех случаях, за исключением тех, когда их использование вызывает трудности:

· на объектах, где целенаправленное изме­нение входных воздействий недопустимо по условиям технологического регламента;

· на объектах, у которых не удается на вре­мя эксперимента стабилизировать все внеш­ние возмущающие воздействия;

· на объектах, имеющих высокий уровень шумов при невозможности выделить в вы­ходном сигнале объекта компоненту отклика объекта на входное воздействие.

Итак, можно сказать, что модель нужна:

· для того чтобы понять, как устроен конкретный объект: какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром;

· для того чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях;

· для того чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воз­действия на объект.

Теоретический метод построения модели.

Методология построения математического описания выделяет шесть положений, которые должны соблюдаться.

Первое положение требует, чтобы сначала была выделена область ,для которой строится модель процесса..

Необходимо для рассматриваемого процесса выбрать такую область, для которой переменные являются постоянными или изменяются немного в пределах области. Необходимо также определите границы этой области.

Этой областью может быть реактор, сечение реактора, часть реактора , газовый пузырек или капелька жидкости. Вообще модель всегда упрощает реальную систему.

Так например, для реактора с мешалкой концентрации и плотность реагирующей массы реактора однородны по всему объему. Это означает, что выходные свойства потока идентичны со свойствами содержания реактора.

Поэтому областью, для которой необходимо составить уравнения математического описания ,может служит сам реактор.

Полная масса в системе дается произведением объема реактора V (м 3 ) на плотность реагирующей смеси ρ (кг/м 3 ). Таким образом масса любого компонента А в реакторе определяется либо терминах фактической массы этого вещества или числа молей(грамм-молекул) в объеме V в виде концентрации вещества A (кг A/м 3 или моль A/м 3 ).

В случае трубчатого реактора концентрации продуктов и реагентов изменятся непрерывно по длине реактора даже, когда реактор работает в установившемся режиме. При этом концентрация в любом сечении реактора будет постоянная и это и есть тот регион ,для которого необходимо составлять уравнения математического описания.

Для некоторых процессов извлечения широко используется представление о ступени процесса, которая и является соответствующей областью.

Второе основное положение гласит:

Необходимо идентифицировать транспортные потоки, которые текут поперек границы системы

После определения области, для которой составляется математическое описание необходимо для нее идентифицировать все вводы(входы) и выводы(выходы). Это могут быть физические расходы , диффузионные потоки, а также потоки межфазной передачи.

Источник

Способы построения моделей

В зависимости от характера и объема априорной информации выделяют два способа построения моделей объектов и систем управления:

Аналитический способ применяется для построения моделей объектов хорошо изученной природы. В этом случае имеется вся необходимая информация, но она представлена в иной форме. Реализуемые при этом модели представляются в виде схем с сосредоточенными параметрами (компонентами). На таких моделях базируются, например, теоретическая механика и теоретическая электротехника.

Читайте также:  Способ построения учебной деятельности это

Методы теории управления абстрагируются от конкретной природы объектов и оперируют более абстрактными – математическими (символьными) моделями.

Аналитический способ моделирования состоит из двух основных этапов:

− построения схемы объекта;

− построение математического описания схемы в требуемой форме.

При этом принципиальные проблемы моделирования решаются на первом (неформальном) этапе, а второй является процедурой преобразования форм представления моделей. Это позволяет разработать и использовать различные компьютерные программы автоматизации составления уравнений по схемам.

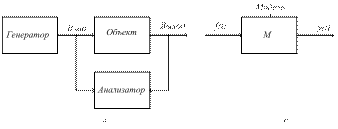
Экспериментальный способ применяется, когда свойства объекта изучены в недостаточной степени либо слишком сложны для аналитического описания. Он заключается в активных экспериментах над объектом или пассивной регистрации его поведения в режиме нормальной эксплуатации (рис. 1.19, а).

Рис. 1.19. Экспериментальное исследование (а) и модель «вход-выход» (б)

В результате обработки данных наблюдений получают модели в требуемой форме. Совокупность этих операций носит название «идентификация объекта». В результате идентификации получают модели «вход-выход» (рис. 1.19, б). Очевидно, что получаемая модель зависит не только от свойств объекта, но и от разнообразия входных сигналов.

Поскольку объект на практике не является «черным ящиком», т.е. о нем что-то известно, то есть возможность комбинировать оба способа: вначале аналитически строить структуру модели и определять приближенные значения параметров, а затем обработкой экспериментальных данных уточнять эти значения.

Используются три основных класса структур моделей систем управления:

– с причинно-следственной структурой;

Модели «вход-выход» отображают зависимость поведения системы от входных воздействий при целостном представлении системы (в виде «черного ящика»). Внутренние переменные (переменные состояния) в них выражаются через входные и выходные переменные.

При построении модели системы с раскрытой причинно-следственной структурой объект или систему предварительно расчленяют на элементы направленного действия и рассматривают их как преобразователи сигналов. Элементы выделяются по функциональному признаку: объект управления, измерительные, преобразовательные и усилительные элементы, устройство управления, исполнительный механизм и т.д. Для каждой части строится своя модель, соединением которых, в соответствии с соединением элементов образуется модель системы. Принципиальной трудностью является создание таких моделей систем с контурами: не зная свойств частей, нельзя знать сигналы на входах этих частей, а без этого нельзя идентифицировать сами части.

В иерархическом представлении структурные модели систем представляются уровнями иерархии (интеграции). При этом модели «вход-выход» являются моделями нулевого уровня причинно-следственной интеграции. Разделение модели «вход-выход»на подсистемы приводит к первому уровню причинно-следственной интеграции и т.д. Дальнейшее раскрытие структур подсистем, каждая из которых снова рассматривается как модель «вход-выход», приводит к многоуровневым (иерархическим) моделям. Часто иерархический подход является единственно возможным для проектирования сложных систем. При этом предполагается, что поведение подсистемы L-го уровня полностью объясняется свойствами подсистем непосредственно нижележащего L-1-го уровня.

Модели среды. Среда на входе системы моделируется автономными системами двух типов:

− генераторами типовых воздействий;

− преобразователями типовых воздействий (фильтрами).

В качестве типовых воздействий используются единичные импульсная и ступенчатая функции, «белый шум». Часто используются также случайные входные воздействия. Некоторые из этих воздействий будут рассмотрены далее.

Детальному исследованию перечисленных типов моделей должно предшествовать рассмотрение математического аппарата, применяемого при исследовании моделей. Поэтому рассмотрим математические средства, применяемые при описании систем управления.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Электронная библиотека

По способу получения математические модели делят на теоретические и эмпирические. Первые получают в результате изучения свойств технического объекта и протекающих в нем процессов, а вторые являются итогом обработки результатов наблюдения внешних проявлений этих свойств и процессов. Один из способов построения эмпирических ММ заключается в проведении экспериментальных исследований, связанных с измерением фазовых переменных ТО, и в последующем обобщении результатов этих измерений в алгоритмической форме или в виде аналитических зависимостей. Поэтому эмпирическая ММ по форме представления может содержать признаки как алгоритмической, так и аналитической математической модели. Таким образом, построение эмпирической ММ сводится к решению задачи идентификации.

При построении теоретических ММ прежде всего стремятся использовать известные фундаментальные законы сохранения таких субстанций, как масса, электрический заряд, энергия, количество движения и момент количества движения. Кроме того, привлекают определяющие соотношения (называемые также уравнениями состояния), в роли которых могут выступать так называемые феноменологические законы (например, уравнение Клайперона-Менделеева состояния идеального газа, закон Ома о связи силы тока в проводнике и падения электрического напряжения, закон Гука о связи деформации и механического напряжения в линейно упругом материале, закон Фурье о связи градиента температуры в теле с плотностью теплового потока и т.п.).

Сочетание теоретических соображений качественного характера с обработкой результатов наблюдения внешних проявлений свойств изучаемого ТО приводит к смешанному типу ММ, называемых полуэмпирическими. При построении таких ММ используют основные положения теории размерностей, в том числе так называемую П-теорему (Пи-теорему): если между n параметрами, характеризующими изучаемый объект, существует зависимость, имеющая физический смысл, то эту зависимость можно представить в виде зависимости между их безразмерными комбинациями , где k – число независимых единиц измерения, через которые можно выразить размерности этих параметров. При этом определяет число независимых (не выражаемых друг через друга) безразмерных комбинаций, обычно называемых критериями подобия.

Объекты, для которых равны значения соответствующих критериев подобия, считают подобными. Например, любой треугольник однозначно определен длинами а, b и с его сторон, т.е. n = 3, a k = 1. Поэтому, согласно П-теореме, множество подобных треугольников можно задать значениями критериев подобия.

В качестве таких критериев можно выбрать безразмерные отношения длин сторон: b/а и с/а или любые два других независимых отношения. Так как углы треугольника однозначно связаны с отношениями сторон и являются безразмерными величинами, то множество подобных треугольников можно определить равенством двух соответствующих углов или равенством угла и отношения длин прилегающих к нему сторон. Все перечисленные варианты соответствуют известным признакам подобия треугольников.

Для успешного применения П-теоремы к построению моделей ТО необходимо располагать полным набором параметров, описывающих изучаемый объект, причем выбор этих параметров должен опираться на аргументированный качественный анализ тех свойств и особенностей ТО, влияние которых существенно в данном конкретном случае. Отметим, что такой анализ необходим при любом способе построения ММ.

Рис. 2.3 Математический маятник

Пример 1

Рассмотрим хорошо известную расчетную схему математического маятника (рис. 2.3) в виде материальной точки массой m, подвешенной на невесомом стержне постоянной длины l, который может свободно вращаться относительно горизонтальной оси, проходящей через точку О. Отклонение маятника на угол φ₀ от его вертикального положения равновесия приведет к возрастанию потенциальной энергии материальной точки на величину:

где g – ускорение свободного падения. Если после отклонения маятник начнет движение, то при отсутствии сопротивления он в силу закона сохранения энергии будет

совершать незатухающие колебания относительно положения равновесия (см. рис. 2.3, точка А). При прохождении положения равновесия скорость (v) материальной точки является наибольшей по абсолютной величине, поскольку в этом положении кинетическая энергия этой точки равна:

Пусть необходимо установить зависимость периода колебаний (Т) маятника (т.е. наименьшего промежутка времени, через который маятник возвращается в некоторое фиксированное положение, не совпадающее с положением равновесия) от параметров m, l, φ₀ и g (параметр v следует исключить из рассмотрения, поскольку его удалось выразить через указанные параметры). Размерности четырех указанных параметров и периода (Т) колебаний можно выразить через k = 3 независимые стандартные единицы физических величин:

Поэтому в силу П-теоремы из n = 5 параметров можно составить безразмерные комбинации, причем угол φ₀, будучи безразмерным, является одной из них. Во вторую безразмерную комбинацию не удается включить массу (m) материальной точки, поскольку единица массы (кг) входит лишь в размерность массы. Следовательно, величина m не является аргументом искомой зависимости, что можно установить и при построении теоретической ММ рассматриваемого маятника.

После исключения параметра m имеем n = 4 и k = 2, т.е. снова , так что наряду с безразмерным параметром φ₀ остальные параметры образуют лишь одну независимую безразмерную комбинацию, которую можно представить в виде .

Таким образом, согласно П-теореме, искомую зависимость можно искать в виде

где – некоторая функция угла φ₀.

Установить вид этой функции в рамках теории размерностей нельзя. Для этого необходимо либо провести эксперимент и обработать его результаты в соответствии с первым равенством (2.3), выявив функциональную зависимость безразмерной комбинации от φ₀, либо воспользоваться теоретической ММ, которая

представляет функцию f в виде полного эллиптического интеграла первого рода. Но даже при неизвестных функциях f (или F) при помощи выражений (2.3) можно получить полезные результаты. Например, если известно значение периода (Т) колебаний для некоторого маятника длиной l при фиксированных значениях g и φ₀, то для маятника длиной l₁ период колебаний будет равен:

Из соображений симметрии (см. рис. 2.3) значение периода колебаний не должно зависеть от знака угла φ₀ первоначального отклонения маятника. Поэтому функция f(φ₀) должна быть четной. Предполагая ее дважды непрерывно дифференцируемой в некоторой окрестности точки φ₀ = 0 и используя формулу Тейлора с остаточным членом в форме Лагранжа, можно записать:

Если при φ₀→0 ограничиться лишь первым слагаемым в правой части этого равенства, то из выражения (2.3) получим .

Таким образом, теория размерностей позволяет установить зависимость для периода бесконечно малых колебаний математического маятника с точностью до постоянного множителя f(0). Соответствующая этому случаю хорошо известная теоретическая ММ приводит к значению f(0) = 2π.

Рис. 2.4 К расчету подъемной силы крыла

Пример 2

К полуэмпирической следует отнести ММ, включающую известную формулу:

для подъемной силы крыла в дозвуковом воздушном потоке, приходящейся на единицу длины размаха крыла. Здесь ρ и v – плотность и скорость набегающего потока; b – так

называемая хорда профиля крыла (рис.

2.4); с_у(α) – безразмерный коэффициент, зависящий от формы профиля крыла и характеризуемого углом атаки (α) направления набегающего потока).

Угол атаки и параметры, определяющие форму профиля крыла, безразмерны. Поэтому можно рассматривать влияние n = 4 размерных параметра Р, ρ, v и b, размерности которых можно выразить через k = 3 независимые стандартные единицы:

[Р] = Н/м = кг/с 2 ; [ρ] = кг/м 3 ; [v] = м/с; [b] = м,

где Н = (ньютон) – производная единица силы. Согласно П-теореме, из этих размерных параметров можно составить лишь одну ( ) независимую безразмерную комбинацию, которую запишем в виде:

Тогда для конкретной формы профиля крыла получим:

где функция f(α) может быть найдена экспериментально путем продувки под различными углами атаки геометрически подобной модели крыла в аэродинамической трубе.

Если безразмерные значения этой функции для фиксированных значений α обозначить через с_у(α)/2, то придем к формуле (2.4). Таким образом, структура выражения (2.4) не противоречит П-теореме.

Комплекс иногда называют динамическим давлением набегающего потока, он равен приращению давления при полном торможении потока, или кинетической энергии единицы объема этого потока. Давление, как и механическое напряжение, измеряют в паскалях (Па = Н/м 2 ). Наряду с выражением (2.4) существует установленная теоретическим путем известная формула Жуковского:

где Г – циркуляция вектора скорости по контуру, охватывающему профиль крыла.

Теоретическая ММ, содержащая выражение (2.5), казалось бы, более совершенна, чем полуэмпирическая ММ, поскольку в отличие от выражения (2.4) не содержит эмпирического коэффициента c_у (α). Однако найти значение Г теоретическим путем удается лишь в редких случаях, часто не представляющих практического интереса, а получить это значение при помощи экспериментальных измерений существенно

сложнее, чем найти значение c_у (α). Поэтому полуэмпирическая ММ в данном случае обладает определенным преимуществом перед теоретической ММ по удовлетворению требованию продуктивности.

Пример 3

Пусть поток несжимаемой жидкости обтекает неподвижное твердое тело заданной формы, имеющее характерный размер l и постоянную температуру T₀ (рис. 2.5). Скорость v и температура Т_ж > T₀ жидкости на большом (по сравнению с l) расстоянии от тела сохраняют постоянные значения. Необходимо при некотором фиксированном положении тела относительно направления вектора (v) скорости найти количество теплоты (Q), передаваемое в единицу времени от жидкости к телу и называемое тепловым потоком.

Рис. 2.5 К расчету теплового потока

Процесс передачи теплоты локализован у поверхности тела и зависит не только от перечисленных параметров, но и от объемной теплоемкости (с) и коэффициента теплопроводности (λ) жидкости, поскольку эти параметры характеризуют способность жидкости подводить тепловую энергию и передавать ее поверхности тела. Подвод тепловой энергии к телу также зависит от распределения скорости жидкости у его поверхности. В случае идеальной (невязкой) жидкости оно однозначно определено фиксированным положением тела относительно вектора v, а для вязкой жидкости зависит и от соотношения между силами вязкости и инерции, характеризуемого коэффициентом вязкости ν, называемым кинематическим и измеряемым в м 2 /с.

При сравнительно близких значениях Т_ж и Т₀ естественно предположить, что тепловой поток зависит не от каждой из этих температур, а от их разности:

Тогда в случае идеальной жидкости имеем n = 6 размерных параметров, размерности которых можно выразить через k = 4 независимые стандартные единицы измерения:

где Дж (джоуль) и Вт (ватт) – единицы энергии (работы) и мощности соответственно, а К (кельвин) – единица температуры в абсолютной шкале. В силу П-теоремы из этих параметров можно составить лишь независимые безразмерные комбинации, например:

В итоге приходим к функциональной зависимости

установленной в 1915 г. Дж. У. Стреттом.

Отношение называют усредненной по площади S поверхности тела плотностью теплового потока и измеряют в Вт/м 2 . Так как для геометрически подобных тел , то зависимость (2.5) можно представить в виде:

где Ki – тепловой критерий Кирпичева и Ре – критерий Пекле. Интенсивность теплообмена на поверхности тела обычно характеризуют усредненным коэффициентом теплоотдачи , измеряемым в .

Тогда вместо зависимости (2.7) получим:

где Nu – критерий (число) Нуссельта.

Вид функции f в зависимостях (2.7) – (2.9) нельзя установить в рамках теории размерностей и его приходится определять путем обработки результатов экспериментов, хотя в некоторых простых случаях удается построить и теоретические ММ процесса теплообмена.

В случае вязкой жидкости имеем n = 7 размерных параметров, размерности которых по-прежнему можно выразить, через k = 4 независимые единицы, т.е. число независимых безразмерных комбинаций равно . К рассмотренным комбинациям следует добавить любую безразмерную комбинацию, включающую новый параметр . Эту комбинацию можно выбрать, например, в виде или . В первом случае ее называют критерием (числом) Рейнольдса и обозначают Re = , а во втором – критерием (числом) Прандтля и обозначают Pr = . Критерий Прандтля характеризует только свойства жидкости, а критерий Рейнольдса – соотношение между инерционными силами и силами вязкого трения.

В итоге вместо зависимости (2.8) получим:

Так как Ре = RePr, то в случае вязкой жидкости критерий Нуссельта может быть представлен функцией любых двух из трех аргументов: Ре, Re, Pr.

Ясно, что при наличии трех и более безразмерных комбинаций параметров построение полуэмпирической ММ существенно усложняется. В этом случае обычно выделяют так называемый определяемый критерий (в нашем примере это Ki или Nu), a остальные критерии относят к определяющим и проводят несколько серий экспериментальных измерений для установления функциональной зависимости определяемого критерия от двух или более определяющих, рассматриваемых в качестве аргументов искомой функции (в зависимостях (2.8) это функции f₁ или f₂).

В каждой серии измерений размерные параметры изменяют таким образом, чтобы изменялось значение лишь одного из определяющих критериев. Тогда обработка результатов такой серии измерений позволяет выявить функциональную зависимость определяемого критерия от одного из аргументов при фиксированных значениях остальных. В итоге в некоторой области изменения значений определяющих критериев удается с некоторой степенью приближения построить искомую функцию, т.е. решить задачу идентификации полуэмпирической ММ.

Отметим, что применение П-теоремы к аналитической ММ, представленной в виде уравнений, позволяет привести эту модель к безразмерной форме и сократить число параметров, характеризующих изучаемый ТО. Это упрощает качественный анализ ММ и позволяет еще до проведения количественного анализа оценить влияние отдельных факторов. Кроме того, безразмерная форма ММ дает возможность представить в более компактном виде результаты ее количественного анализа.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник