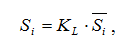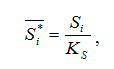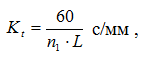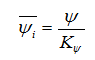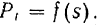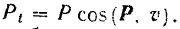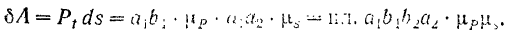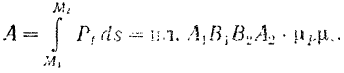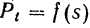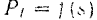Теоретическая механика графический способ

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

• 1. Аксиомы и понятие силы статики
• 2. Связи и реакции связей
• 3. Определение равнодействующей геометрическим способом
• 4. Определение равнодействующей аналитическим способом
• 5. Пара сил. Момент силы

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

3. Определение равнодействующей геометрическим способом

Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.

Необходимо определить равнодействующую системы сходящихся сил (F₁; F₂; F₃;…; F_n), где n — число сил, входящих в систему.

В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.

Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.

При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.

Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.

Многоугольник сил строится в следующем порядке.

1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.

2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.

Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.

Если в системе три силы, образуется треугольник сил.

Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).

Задачи решаются в следующем порядке.

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения определить величины векторов (сторон многоугольника) с помощью геометрических зависимостей.

Источник

iSopromat.ru

Графический метод кинематического исследования механизмов сводится к решению задач построения диаграмм (графиков) движения исследуемого звена или точки.

При этом строятся диаграммы перемещений, скоростей и ускорений – поэтому данный метод часто называют методом кинематических диаграмм.

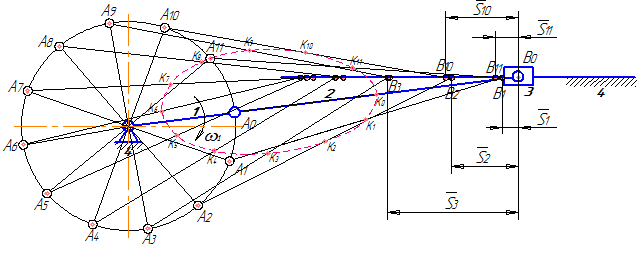
Исследование начинается с построения различных положений механизма. Строится “N” последовательных положений механизма, которые он занимает в процессе работы в пределах одного цикла (обычно один полный оборот входного звена). Построение ведется строго в масштабе K_L.

Количество положений механизма “N” выбирается в зависимости от необходимой точности исследования. При чисто графическом решении задачи обычно принимают N=12. Это обеспечивает в большинстве случаев достаточную практическую точность при относительно небольшом количестве построений. Большее количество положений делает метод весьма громоздким, приводит к значительному затемнению чертежа и трудности его чтения.

При использовании графического метода в качестве алгоритма решения задачи с помощью ЭВМ количество положений механизма, выбираемых для исследования, не имеет ограничений.

Построение отдельных положений механизма ведется по группам Ассура и обычно сводится к графическому решению элементарных геометрических задач.

После построения “N” положений механизма строится диаграмма перемещений исследуемого звена. Одно из положений механизма принимается за нулевое (в качестве нулевого положения можно назначать любое положение механизма, но при чисто графическом решении задачи обычно в качестве нулевого принимают положение механизма, в котором исследуемое звено занимает одно из своих крайних положений).

От нулевого положения производится нумерация остальных положений механизма, последовательно занимаемых им в процессе работы (на входном звене нумерация должна совпадать с направлением его движения).

Отметив последовательные положения исследуемого звена, измеряют расстояние до каждого из них от нулевого (см. рисунок 10) и определяют истинные значения перемещений через масштаб чертежа:

где
_
S_i – отрезок, измеренный на чертеже в миллиметрах,
S_i – истинное перемещение звена в метрах.
В общем случае для построения диаграммы назначают масштаб перемещений K_S и определяют значения ординат, соответствующие перемещениям звена в каждом положении механизма:

где
__
S * _i – значение ординаты на диаграмме перемещений в миллиметрах для каждого положения исследуемого звена (для каждого положения механизма – см. рисунок 11).

Примечание: если величины отрезков, изображающих перемещение звена на чертеже, подходят для построения диаграммы, то можно без дополнительных расчетов откладывать их по оси ординат на диаграмме перемещений для соответствующих положений. При этом

Ось абсцисс на диаграммах движения является осью времени t. Однако при построении диаграмм обычно отмечаются положения механизма, для которых производится исследование, а затем (в зависимости от выбранного отрезка на оси абсцисс, соответствующего полному циклу работы механизма, и скорости входного звена) рассчитывается масштаб времени K_t:

где
n₁ – частота вращения входного звена в об/мин
L – отрезок на оси абсцисс диаграммы перемещений, соответствующий полному обороту входного звена.

Двойным дифференцированием диаграммы перемещений получают диаграмму скоростей и диаграмму ускорений исследуемого звена или точки.

Так как диаграмма перемещений строится по точкам и уравнение полученной кривой неизвестно, то дифференцирование проводится графическими методами.

Если исследуемое звено является коромыслом (т.е. совершает возвратно-вращательное движение), то строится диаграмма угловых перемещений (углов поворота) данного звена, а при дифференцировании соответственно получают диаграмму угловых скоростей и диаграмму угловых ускорений данного звена.

Примечание: при измерении углов поворота исследуемого звена надо иметь ввиду, что, независимо от масштаба построения механизма, углы на чертеже имеют истинную величину. Углы измеряют в радианах и переводят в отрезки на диаграмме через масштаб углов поворота:

где
__
Ψ — отрезок на диаграмме угловых перемещений в мм, соответствующий углу поворота Ψ исследуемого звена;
K_Ψ — масштаб углов поворота в рад/мм.

Для построения траектории движения какой-либо точки надо отметить положение данной точки во всех N положениях механизма и последовательно соединить полученные точки плавной кривой.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Графический способ вычисления работы

Графический способ вычисления работы

Вычисление работы си ты на конечном пути по установленным формулам, без знания закона движения точки приложения силы, возможно лишь в частных случаях (например, при постоянной силе).

Для вычисления же работы силы в общем случае, когда сила может зависеть от времени, координат и скорости, нужно знать закон движения точки приложения силы. Только в этом случае можно выразить, как мы видели при решении задачи 86, все переменные в функции времени 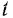и вычислить соответствующий интеграл.

Если же закон движения точки приложения силы неизвестен, то для вычисления работы силы нужно сначала найти этот закон, т. е. решить вторую основную задачу динамики.

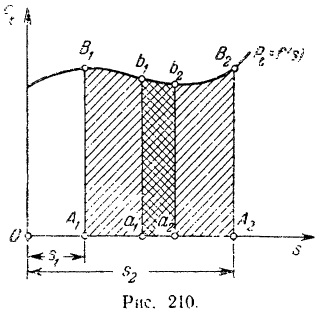
На практике для определения работы часто пользуются графическим способом, используя для этой цели график зависимости

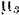
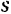
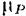
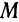
По оси абсцисс этого графика (рис. 210) отложены, в некотором масштабе значения дуговой координаты точки приложения силы, а по оси ординат, также в каком-то масштабе , соответствующие им значения проекции этой силы на направление скорости точки , т.е.

Элементарная работа силы будет равна

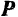
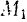
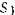
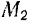
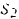
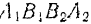
Работа силы на конечном перемещении ее точки приложения из положения с дуговой координатой в положение с координатой будет выражаться в некотором масштабе площадью фигуры (рис. 210):

Работа силы на некотором перемещении ее точки приложения выражается в определенном масштабе площадью фигуры, ограниченной осою абсцисс, кривой

и двумя ординатами, соответствующими начальному и конечному положениям точки приложение силы.

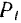
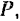
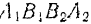
На рис. 210 алгебраические значения касательной составляющей силы отложены и положительную сторону соответствующей оси и потому работа силы изображаемая площадью фигуры , будет положительной. Если же построенная кривая

будет расположена от оси абсцисс в сторону отрицательных значений 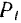, то соответствующая площадь будет изображать отрицательную работу.

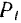
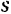
К графическому способу определения работы силы приходится прибегать в тех случаях, когда нам известны значения силы только для отдельных значении , установление же аналитической зависимости

затруднительно или даже невозможно. В ряде случаев (например, при определении работы пара или газа в цилиндрах паровой машины или двигателя) график зависимости

получается автоматически, при помощи самопишущих приборов, называемых индикаторами.

В заключение отметим следующее обстоятельство.

Хотя установленное в механике понятие работы (называемой иногда механической работой) и возникло из повседневного опыта, но оно не всегда совпадает с тем, что понимают под работой с физиологический точки зрения. Так, человек, неподвижно держащий па вытянутых руках тяжелый груз, не совершает, очевидно, с точки зрения механики, никакой работы (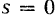). С физиологической же точки зрения он совершает, конечно, определенную работу.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник