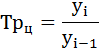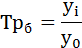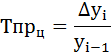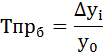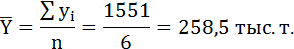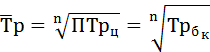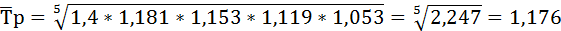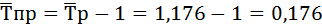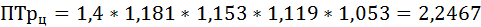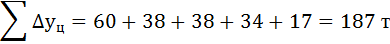Темп прироста базисным способом формула

Формула темпа прироста

Понятие и значение темпа прироста

Темп прироста используется при анализе какого-либо ряда динамики. Формула темпа прироста часто применяется в статистике и экономике в паре с таким показателем, как темп роста (в процентном соотношении).

Если в результате расчета получается положительная величина, то можно говорить об увеличивающемся темпе прироста, при отрицательном же значении происходит снижение темпа исследуемого значения, если сравнивать его с предыдущим (базисным) периодом.

Формула темпа прироста часто применяется в анализе инвестиционных проектов. Также этот показатель часто используется муниципальными организациями при расчетах:

• вычисление прироста населения;
• будущей потребности в зданиях;
• объемов оказания услуг и др.

Формула темпа прироста

Для расчета темпа прироста нужно найти отношение исследуемого показателя к предыдущему (базисному), далее из получаемого результата вычесть единицу. Окончательный результат умножается на 100, для того, что бы выразить итог в процентах. Формула темпа прироста по первому способу выглядит так:

Тп=((Пип/Пбп)-1)*100%

Здесь Тп – темп прироста,

Пбп – показатель базисного периода,

Пип – показатель исследуемого периода.

В случае, когда вместо фактического значения анализируемых показателей известно только значение абсолютного прироста, применяют альтернативную формулу. При этом находят процентное отношение абсолютного прироста к тому уровню, в сравнении с которым он и рассчитывался.

Тп=((Пип-Пбп)/Пбп)*100%

Здесь Тп – темп прироста,

Пбп – показатель базисного периода,

Пип – показатель исследуемого периода.

Отличие темпа роста и темпа прироста

Большую сложность для учащихся представляет отличие темпа роста от темпа прироста. Выделим несколько положений, в которых заключается разница между этими величинами:

1. Формула темпа роста и формула темпа прироста рассчитываются по разным методикам.
2. Темп роста отражает количество процентов одного показателя относительно другого, а темп прироста показывает, насколько он вырос.
3. На основании расчетов по формуле темпа роста можно рассчитать темп прироста, при этом по формуле темпа прироста расчет темпа роста не проводят.
4. Темп роста не принимает отрицательное значение, при этом темп прироста может получаться как положительной, так и отрицательной величиной.

Примеры решения задач

Задание

Для предприятия ООО «Севермет» даны следующие показатели, представленные за 2015 и 2016 год:

2015 год – 120млн. рублей,

2016 год – 110,4млн. рублей.

Известно, что в 2017 году величина дохода увеличилась в сравнении с 2016 годом на 25 млн. рублей.

На основе имеющихся данных рассчитать темп роста и прироста, сделав при этом выводы.

Решение Определим темп роста в процентах за 2015 и 2016 год, для чего нужна формула темпа роста:

Здесь Тр – темп роста,

П2015 – показатель за 2015 год,

П2016 – показатель за 2016 год.

Тр=110,4млн. руб./120млн. руб. * 100% = 92 %

Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула темпа прироста:

Или второй способ:

Рассчитаем показатели за 2017 год

Тр=(120 млн. руб. + 25 млн. руб.)/120 млн. руб.= 1,21 (или 121 %)

Тп=(145 млн. руб./120 млн. руб)-1=0,208 (или 20,8%)

Вывод. Мы видим, что темп роста при сравнении 2015 и 2016 года составил 92%. Это означает, что прибыль предприятия в 2016 году уменьшилась на 92%в сравнении с 2015 годом. При расчете темпа прироста получилась отрицательная величина (-8%), что говорит о том, что прибыль компании в 2016 году (при сравнении с 2015 годом) уменьшилась на 8%. В 2017 году прибыль составила 121% в сравнении с 2016 годом. При расчете темпа прироста мы видим, что он составил 20,8%. Положительная величина говорит об увеличении прибыли именно на это количество процентов.

Ответ При сравнении 2015 и 2016 года Тр=92 %, Тп=8%, при сравнении 2016 и 2017 года Тр=121%, Тп=20,8%.

Задание

Рассчитать прирост заработной платы на предприятии ООО «Севермет» за 2015 и 2016 год. Даны следующие показатели:

Заработная плата 2015 год – 31,5 тыс. руб.,

заработная плата 2016 год – 33 тыс. руб.,

Решение Темп прироста обозначает процентное соотношение изменения величины в текущем периоде в сравнении с предыдущим. Для расчета нужна формула:

Вывод: Таким образом, мы видим, что темп прироста составил 4,8 %, что означает, что заработная плата в 2016 году по сравнению с 2015 годом увеличилась на 4,8%.

Источник

Задача №56. Расчёт аналитических показателей динамики

Добыча нефти характеризуется следующими данными:

Годы	Добыча нефти, тыс. т
1-ый	150
2-ой	210
3-ий	248
4-ый	286
5-ый	320
6-ой	337

Произвести анализ ряда динамики по:

1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;

2) средний уровень и среднегодовой темп ряда динамики;

3) показать взаимосвязь между цепными и базисными показателями.

Решение:

Абсолютный прирост цепной (Δy_ц) – это разность между текущим уровнем ряда и предыдущим:

Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:

= 210 – 150 = 60 тыс. т.

В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:

Δy_{ц 3-й год} = 248 – 210 = 38 тыс. т.

Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.

Абсолютный прирост базисный (Δy_б) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:

Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.

Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:

Δy_б = 210 – 150 = 60 тыс. т

в 3-ем году базисный абсолютный прирост равен:

Δy_б = y₃ – y₂ = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).

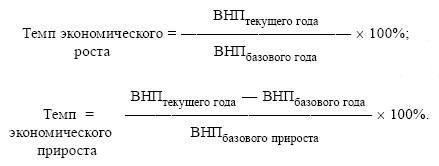
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:

(гр. 5 расчётной таблицы);

базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:

(гр. 4 расчётной таблицы).

Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:

Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:

Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:

или как разность между темпами роста и 100%, если темпы роста выражены в процентах:

Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).

Годы	Добыча нефти, тыс. т	Абсолютный прирост базисный, тыс. т	Абсолютный прирост цепной, тыс. т	Темп роста базисный, %	Темп роста цепной, %	Темп прироста базисный, %	Темп прироста цепной, %
А	1	2	3	4	5	6	7
1-ый	150	0	—	100,00	—	—	—
2-ой	210	60	60	140,00	140,0	40,00	40,0
3-ий	248	98	38	165,33	118,1	65,33	18,1
4-ый	286	136	38	190,67	115,3	90,67	15,3
5-ый	320	170	34	213,33	111,9	113,33	11,9
6-ой	337	187	17	224,67	105,3	124,67	5,3

Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.

2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:

Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической

где ПТр – произведение цепных темпов роста (в коэффициентах),

– конечный базисный темп роста (в коэффициентах),

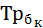
n – число темпов.

Среднегодовой темп прироста ряда динамики:

Добыча нефти ежегодно возрастала в среднем на 17,6%.

3) Между цепными и базисными темпами роста имеется взаимосвязь:

произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.

Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:

Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.

Источник

СПИСОК ЛИТЕРАТУРЫ ОНЛАЙН

Как рассчитать темп роста и прироста?

Темп роста — это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).

Темп прироста — это прирост какой либо изучаемой величины за один временной период за вычетом 100%.

Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста — всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.

Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.

Расчет темпа роста и прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

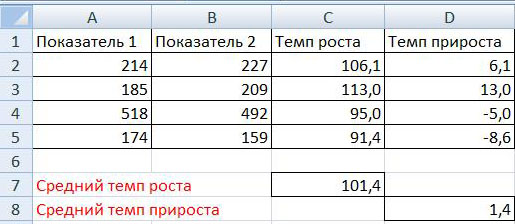
На рисунке представлен пример расчета темпа роста и прироста:

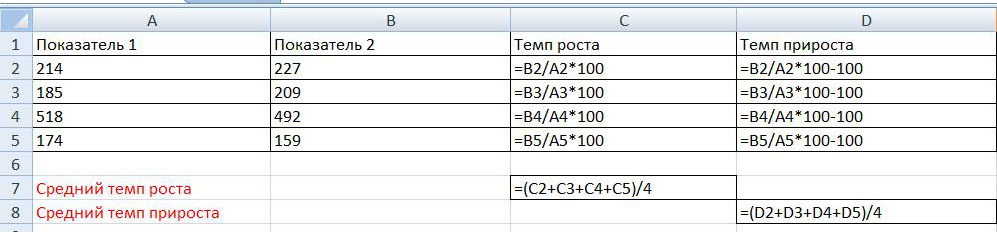
Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:

На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.

Расчет средних темпов роста и прироста

Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста — сумма темпов прироста за все периоды делится на количество периодов.

Расчет базисного темпа роста и базисного темпа прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

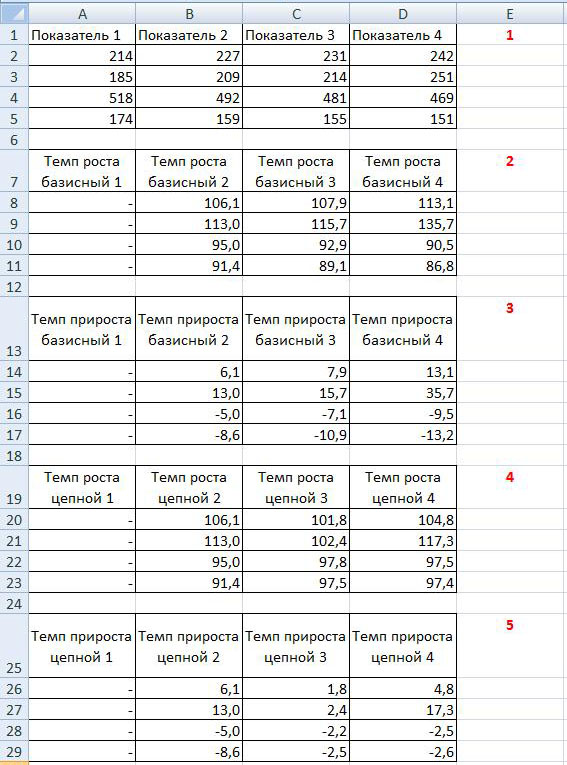
На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):

Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя.

В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.

Расчет цепного темпа роста и цепного темпа прироста

На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).

Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя.

То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.

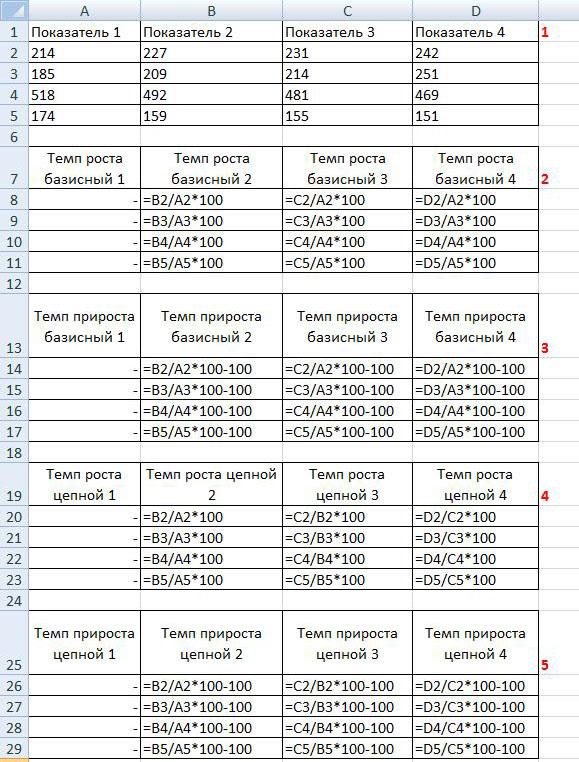
Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:

Обратите внимание, что при расчете базисного и цепного показателей, значения базисного и цепного темпов роста и прироста равны, так как при избрании в качестве базисного показателя первого из ряда, они рассчитываются одинаково.

Источник