Темп изменения цепной способ

Ряды динамики

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

1. По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
2. По форме представления — ряды абсолютных, относительных и средних величин.
3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
4. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

• абсолютное изменение (абсолютный прирост);
• относительное изменение (темп роста или индекс динамики);
• темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого	-2,3	0,984	-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

В нашем примере про число жителей России подтверждается правильность расчета абсолютных изменений: = — 2,3 рассчитана в итоговой строке 4-го столбца, а = — 2,3 – в предпоследней строке 3-го столбца расчетной таблицы.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.

• 
• 
• 

• Разработка интернет-магазина
• Редизайн сайта эвакуации
• Редизайн сайта доставки суши

Источник

Показатели изменения уровней ряда динамики

Поможем написать любую работу на аналогичную тему

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

– абсолютное изменение (абсолютный прирост);

– относительное изменение (темп роста или индекс динамики);

– темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Абсолютное изменение (абсолютный прирост) уровней рассчитывается как разность между двумя уровнями ряда по формуле (74) – для базисного способа сравнения или по формуле (75) – для цепного. Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше уровня какого-либо предшествующего периода, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

; (74) . (75)

В табл. 28 в столбце 3 рассчитаны базисные абсолютные изменения по формуле (74), а в столбце 4 – цепные абсолютные изменения по формуле (75).

Источник

Порядок расчета показателей цепным способом

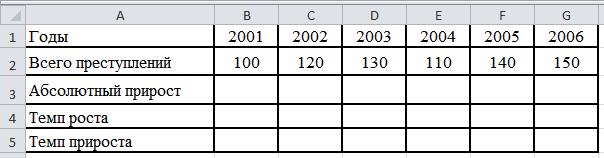
Динамика уличных преступлений в городе N представлена в таблице.

Годы

Всего преступлений

Необходимо рассчитать показатели анализа динамики: абсолютный прирост (снижение), темпы роста (снижения), темпы прироста (снижения). Расчет произвести цепным способом.

При помощи программы Excel сформируйте таблицу следующего вида:

Абсолютный прирост, темп роста и темп прироста для 2001 года рассчитать не представляется возможным, так как отсутствуют данные предыдущего периода (2000 г.), поэтому в графах таблицы (в соответствии с правилами оформления статистических таблиц) указываем н.д. (нет данных) или ставим прочерк. Отрицательные значения, полученные при расчетах, показывают, что показатель динамики снизился по сравнению с предыдущим периодом.

В соответствии с заданием расчет произведем цепным способом.

Абсолютный прирост для 2002 г. рассчитываем как разность между уровнями ряда текущего (2002 г.) и предыдущего периода (2001 г.), т.е. 120 — 100 = 20. Для этого в ячейку С3 вводим формулу =С2-В2. Далее воспользуемся функцией автозаполнения и «протянем» по строке маркер, начиная с ячейки С3 и до ячейки G3.

Темп роста рассчитаем как отношение уровня ряда в текущем периоде (2002 г.) к уровню ряда в предыдущем периоде (2001 г.)., т.е. (120 / 100) · 100 % = 120 %. Для этого в ячейку С4 вводим формулу =С2/В2, далее задаем формат ячейки – процентный. Снова воспользуемся функцией автозаполнения и «протянем» по строке маркер, начиная с ячейки С4 и до ячейки G4.

Темп прироста рассчитаем как отношение абсолютного прироста текущего периода (2002 г.) к уровню ряда предыдущего периода (2001 г.), т.е. (20 / 100) · 100 % = 20 %. Для этого в ячейку С5 вводим формулу =С3/В2, далее задаем формат ячейки – процентный. Снова воспользуемся функцией автозаполнения и «протянем» по строке маркер, начиная с ячейки С5 и до ячейки G5.

Источник

Как рассчитать темп роста в процентах

Похожие публикации

Важнейшим показателем эффективности производства в анализе финансовой ситуации в компании является показатель темпа роста. Поговорим об особенностях его расчета.

Как рассчитать темп роста: формула

Этот термин показывает изменение значения любого экономического или статистического показателя в текущем периоде к его начальному значению (являющемуся базовым) за определенный временной промежуток. Измеряется он в процентах или коэффициентах.

Например, при сравнении объема выпуска товаров на конец года (допустим, в значении 100000 руб.) к показателю объема на начало года (70000 руб.) темп роста находят отношением конечного значения к начальному: 100000 / 70000 = 1,428. Индекс роста в примере составил 1,429. Это означает, что на конец года объем выпуска составил 142,9%.

Как рассчитать темп роста в процентах — формула:

ТР = П_т / П_б х 100%,

где П_к и П_б – показатели значений текущего и базового периодов.

Темп роста показывает интенсивность изменений какого-либо процесса по отношению к его начальному (базовому) значению. Результат вычислений – один из трех вариантов:

ТР больше 100%, следовательно, конечное значение возросло в сравнении с начальным, т.е. налицо рост показателя;

ТР = 100%, т.е. изменений ни в большую, ни в меньшую сторону не произошло – показатель остался на прежнем уровне;

ТР меньше 100%, значит, анализируемый показатель снизился к началу периода.

Приведем примеры, как рассчитать темп роста в процентах по каждому варианту расчета, объединив исходные данные в таблицу:

Объем выпуска в тыс. руб.

Такой темп роста называют базисным, поскольку база сравнения по периодам остается неизменной – показатель на начало периода. Если же сравнительная база изменяется, а темп роста вычисляют отношением текущего значения к предыдущему (а не базисному), то этот показатель будет цепным.

Как рассчитать цепные темпы роста

Рассмотрим пример расчета базисного и цепного темпов роста:

Период

Объем в тыс.руб.

Темп роста в %

базисный

цепной

Цепные темпы роста характеризуют насыщенность изменения уровней от квартала к кварталу, базисные же отражают ее в целом за весь временной интервал (показатель 1 квартала – база сравнения).

Сравнивая показатели в приведенном примере, можно отметить, что ряд значений, рассчитанных к началу периода, имеет меньшую амплитуду колебаний, чем цепные показатели, вычисления которых привязаны не к началу года, а к каждому предшествующему кварталу.

Как рассчитать темпы прироста

Кроме расчета темпов роста, принято высчитывать и темпы прироста. Эти значения также бывают базисными и цепными. Базисный прирост определяют как отношение разности показателей текущего и базового периодов к значению базового периода по формуле:

Цепной прирост рассчитывают как разность между текущим и предыдущим показателями, деленную на темп роста предыдущего периода:

Более простым способом расчета является формула: ∆ ТР = ТР – 100%, где расчетные показатели темпа роста уменьшаются на 100%, т. е. исходную величину. Показатель темпа прироста в отличие от значений темпа роста может иметь отрицательное значение, поскольку темп роста (или снижения) показывает динамику изменений показателя, а темп прироста говорит о том, какой характер они носят.

Продолжая пример, рассчитаем приросты объемов в рассматриваемых периодах:

Источник