Тема урока функции способы задания функции 10 класс

Открытый урок по теме: «Функция: понятие, способы задания, основные характеристики. Обратная функция. Суперпозиция функций».
план-конспект урока по алгебре (10 класс) по теме

Изложены основные характеристики функции. Приведены определения обратной функции и сложной функции.

Скачать:

Вложение	Размер
основные свойства функций	191.5 КБ

Предварительный просмотр:

Тема: «Функция: понятие, способы задания, основные характеристики. Обратная функция. Суперпозиция функций».

«Изучать что-либо и не задумываться над

выученным — абсолютно бесполезно.

Задумываться над чем-либо, не изучив

предварительно предмет раздумий-

Цель и психолого-педагогические задачи урока :

1. Общеобразовательная (нормативная) цель : повторить со студентами определение и свойства функции. Ввести понятие суперпозиции функций.
2. Задачи математического развития студентов : на нестандартном учебно-математическом материале продолжить развитие ментального опыта учащихся, содержательной когнитивной структуры их математического интеллекта, в том числе, способностей к логико-дедуктивному и индуктивному, аналитическому и синтетическому обратимому мышлению, к алгебраическому и образно-графическому мышлению, к содержательному обобщению и конкретизации, к рефлексии и самостоятельности как метакогнитивной способности студентов; продолжить развитие культуры письменной и устной речи как психологических механизмов учебно-математического интеллекта.
3. Воспитательные задачи : продолжить личностное воспитание у студентов познавательного интереса к математике, ответственности, чувства долга, академической самостоятельности, коммуникативного умения сотрудничать с группой, преподавателем, согруппниками; аутогогической способности к соревновательной учебно-математической деятельности, стремления к высоким и высшим ее результатам (акмеический мотив).

Тип урока : изучение нового материала; по критерию ведущего математического содержания — урок-практикум; по критерию типа информационного взаимодействия учащихся и преподавателя – урок сотрудничества.

1) Кудрявцев Л.Д. Курс математического анализа: Учеб. для студентов университетов и вузов. В 3 т. Т. 3. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1989. – 352 с. : ил.

2) Демидович Б.П. Сборник задач и упражнений по математическому анализу. – 9-е изд. – М.: Издательство «Наука», 1977.

1.Объявление темы и главной образовательной цели урока; стимулирование чувства долга, ответственности, познавательного интереса студентов при подготовке к сессии.

2.Повторение материала по вопросам.

a) Дать определение функции.

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости между элементами двух множеств.

Пусть даны два непустых множества и . Соответствие f, которое каждому элементу сопоставляет один и только один элемент , называется функцией и записывается y = f(x). Говорят еще, что функция f отображает множество на множество .

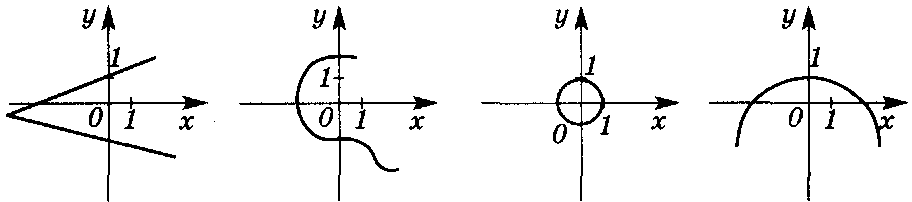
Например, соответствия f и g, изображенные на рис.1 а и б, являются функциями, а на рис.1 в и г – нет. В случае в – не каждому элементу соответствует элемент . В случае г не соблюдается условие однозначности.

Множество X называется областью определения функции f и обозначается D(f) . Множество всех называется множеством значений функции f и обозначается E(f).

б) Числовые функции. График функции. Способы задания функций.

Пусть задана функция .

Если элементами множеств и являются действительные числа, то функцию f называют числовой функцией . Переменная x при этом называется аргументом или независимой переменной, а y – функцией или зависимой переменной (от x). Относительно самих величин x и y говорят, что они находятся в функциональной зависимости .

Графиком функции y = f(x) называется множество всех точек плоскости Oxy , для каждой из которых x является значением аргумента, а y – соответствующим значением функции.

Чтобы задать функцию y = f(x), необходимо указать правило, позволяющее, зная x , находить соответствующее значение y.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ : функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции y = f(x) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл.

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию y = f(x).

Графический способ : задается график функции.

Преимуществом графического задания является его наглядность, недостатком – его неточность.

Табличный способ : функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

в) Основные характеристики функции.

1. Функция y = f(x),определенная на множестве D, называется четной , если выполняются условия и f(-x) = f(x); нечетной , если выполняются условия и f(-x) = -f(x).

График четной функции симметричен относительно оси Oy, а нечетной – относительно начала координат. Например, – четные функции; а y = sinx, – нечетные; y = x-1, – функции общего вида, т.е. не четные и не нечетные.

2.Пусть функция y = f(x) определена на множестве D и пусть . Если для любых значений аргументов из неравенства вытекает неравенство: , то функция называется возрастающей на множестве ; если , то функция называется неубывающей на ; то функция наз. убывающей на ; — невозрастающей .

Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными . Интервалы, в которых функция монотонна, называются интервалами монотонности .

3. Функция y = f(x), определенная на множестве D, называется периодической с периодом T>0, если при каждом x D значение (x+T) D и выполняется равенство f(x+T) = f(x).

Для построения графика периодической функции периода T достаточно построить его на любом отрезке длины T и периодически продолжить его во всю область определения.

Отметим основные свойства периодической функции.

1) Алгебраическая сумма периодических функций, имеющих один и тот же период T, есть периодическая функция с периодом T.

2) Если функция f(x) имеет период T, то функция f(ax) имеет период T/a.

г) Обратная функция.

Пусть задана функция y = f(x) с областью определения D и множеством значений E. Если каждому значению соответствует единственное значение , то определена функция x = z(y) с областью определения E и множеством значений D. Такая функция z(y) называется обратной к функции f(x) и записывается в следующем виде: . Про функции y = f(x) и x = z(y) говорят, что они являются взаимно обратными. Чтобы найти функцию x = z(y), обратную к функции y = f(x), достаточно решить уравнение f(x) = y относительно x.

1. Для функции y = 2x обратной функцией является функция x = ½ y;
2. Для функции обратной функцией является функция .

Из определения обратной функции вытекает, что функция y = f(x) имеет обратную тогда и только тогда, когда f(x) задает взаимно однозначное соответствие между множествами D и E. Отсюда следует, что любая строго монотонная функция имеет обратную . При этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).

1. Изучение нового материала.

Пусть функция y = f(u) определена на множестве D, а функция u = z(x) на множестве , причем для соответствующее значение . Тогда на множестве определена функция u = f(z(x)), которая называется сложной функцией от x (или суперпозицией заданных функций, или функцией от функции ).

Переменную u = z(x) называют промежуточным аргументом сложной функции.

Например, функция y = sin2x есть суперпозиция двух функций y = sinu и u = 2x. Сложная функция может иметь несколько промежуточных аргументов.

4. Решение нескольких примеров у доски.

5. Заключение урока.

1) теоретико-прикладные итоги практического занятия; дифференцированная оценка уровня ментального опыта учащихся; уровня усвоения ими темы, компетентности, качества устной и письменной математической речи; уровня проявленного творчества; уровня самостоятельности и рефлексии; уровня инициативы, познавательного интереса к отдельным методам математического мышления; уровней сотрудничества, интеллектуальной состязательности, стремления к высоким показателям учебно-математической деятельности и др.;

2) объявление аргументированных отметок, поурочного балла.

Источник

Числовые функции. Определение и способы задания
презентация к уроку по алгебре (10 класс) на тему

Презентация к уроку математики 10 класса. Числовые функции. Определение и способы задания.

Скачать:

Вложение	Размер
01._chislovye_funktsii._opredelenie_i_sposoby_zadaniya.pptx	2.49 МБ

Предварительный просмотр:

Подписи к слайдам:

Числовые функции. Определение и способы задания.

Напомним Если даны числовое множество и правило , позволяющее поставить в соответствие каждому элементу из множества определенное число , то говорят, что задана функция с областью определения : – область определения функции; – независимая переменная или аргумент; – зависимая переменная; множество всех значений , называют областью значений функции и обозначают .

Если дана функция , и на координатной плоскости отмечены все точки вида , где , а , то множество этих точек называют графиком функции , .

Графики некоторых функций прямая

Зная график функции с помощью геометрических преобразований можно построить график функции . Для этого надо сделать параллельный перенос графика функции на вектор , то есть на вправо, если , и влево, если на вверх, если , и вниз, если .

Пример -4 0 1 2 3 4

Задать функцию – указать правило , которое поз- воляет по произвольно выбранному значению вычислить соответствующее значение . Чаще всего это правило связано с формулой (например ). Такой способ задания функции называется аналитическим .

Пример Пусть – некоторая линия на координатной плоскости

Тем самым на отрезке задана функция . Такой способ задания функции называют графическим . Заметим, что если функция была задана аналитически и нам удалось построить ее график, то тем самым мы фактически осуществили переход от аналитического способа задания функции к графическому.

Табличный способ задания функции – с по-мощью таблицы, в которой указаны значения функции для конечного множества значений аргумента. Например : 5 7 8 9 10 12 5 7 4 6 5 7 8 9 10 12 5 7 4 6

Словесный способ задания функции – способ, при котором правило задания функции описывается словами.

Пример: Функция задана на множестве всех неотрицательных чисел с помощью следующего правила: каждому числу ставится в соответствие первая цифра после запятой в десятичной записи числа . Если , , то 6, так как =0 ,(6) то , так как

По теме: методические разработки, презентации и конспекты

Открытый урок. Способы задания числовой функции.

Цели урока: 1. Образовательная: продолжить формирование умений и навыков работы с числовыми функциями:Навыков задания функций различными способами;Навыков перехода от одного способа задания функ.

Конспект урока математики (по новым ФГОС), по теме:Понятие функции. Область определения и множество значений функции. Способы задания функции.

Конспект урока математики по новым ФГОС.Тема урока: Понятие функции. Область определения и множество значений функции. Способы задания функции.

«Определение числовой функции. Область определения и область значений функции»

Уточнить понятие функции, её основных характеристик — области определения и области (множества) значений.

«Определение числовой функции. Область определения и область значений функции» Урок математики Корниенко Анны Михайловны МБОУ СОШ № 9 Староминская

Уточнить понятие функции, её основных характеристик — области определения и области (множества) значений.

Определение числовой функции. Область определения, область значений функции.

презентация к уроку.

Урок алгебры в 9 классе «Определение числовой функции. Область определения и область значений функции»

Урок «Определение числовой функции. Область определения и область значений функции» по учебнику А. Г. Мордковича. Тип урока: обобщение и систематизация знанийЗадачи: создать усл.

Источник

Конспект урока по математике «Функция и способы ее задания»

Описание разработки

Задачи:

Определить виды величин.

Напомнить понятие функции, ее области определения и множества значений.

Рассмотреть способы задания функции.

Закрепить полученные знания при решении задач.

Ход урока

Сообщение темы и цели урока.

Повторение изученного материала.

В математике одним из важных понятий является понятие ФУНКЦИИ. Как вы понимаете это слово? Вспомним пройденное за курс алгебры 7 — 9 класса. (Ответы учеников. )

Функцией у от х называется такое соответствие между переменными х и у, при котором каждому значению х соответствует не более одного значения у.

Функцию можно задать формулой, таблицей, графиком.

Устная работа

Среди данных линий найти такую, которая является графиком какой — либо функции.

Решение: На первых трех графиках имеются точки с одинаковыми абсциссами и разными ординатами. Это значит, что на этих линиях одному и тому же значению х соответствует более одного значения у, то есть эти линии не являются графиками функций. На четвертом графике каждому значению х соответствует не более одного значения у – это график функции.

Среди данных таблиц найдите такую, которая является таблицей функции.

Решение: В первой и второй таблице имеются значения х, которым соответствуют два разных значения у, то есть эти таблицы не являются таблицами функций. В третьей таблице каждому значению х соответствует не более одного значения у – это таблица функции.

Изучение нового материала

Рассмотрим понятие функции более широко.

В своей практической деятельности человек сталкивается с величинами различной природы: длина, площадь, объем, масса, температура, вес и т. д.

В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т. е. не меняются; другие наоборот, принимают различные значения.

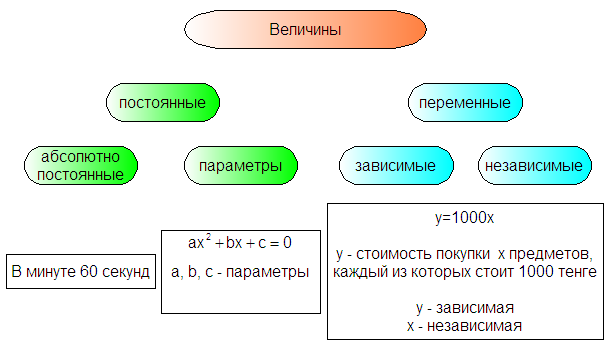
Все величины, изучаемые в математике, делятся на постоянные и переменные. (Формулируются соответствующие определения)

Весь материал – смотрите документ.

Содержимое разработки

Тема: Функция и способы ее задания.

Определить виды величин.

Напомнить понятие функции, ее области определения и множества значений.

Рассмотреть способы задания функции.

Закрепить полученные знания при решении задач.

Сообщение темы и цели урока.

Повторение изученного материала.

В математике одним из важных понятий является понятие ФУНКЦИИ. Как вы понимаете это слово? Вспомним пройденное за курс алгебры 7-9 класса. (Ответы учеников.)

Функцией у от х называется такое соответствие между переменными х и у, при котором каждому значению х соответствует не более одного значения у.

Функцию можно задать формулой, таблицей, графиком.

Среди данных линий найти такую, которая является графиком какой-либо функции.

Решение: На первых трех графиках имеются точки с одинаковыми абсциссами и разными ординатами. Это значит, что на этих линиях одному и тому же значению х соответствует более одного значения у, то есть эти линии не являются графиками функций. На четвертом графике каждому значению х соответствует не более одного значения у – это график функции.

Среди данных таблиц найдите такую, которая является таблицей функции.

Решение: В первой и второй таблице имеются значения х, которым соответствуют два разных значения у, то есть эти таблицы не являются таблицами функций. В третьей таблице каждому значению х соответствует не более одного значения у – это таблица функции.

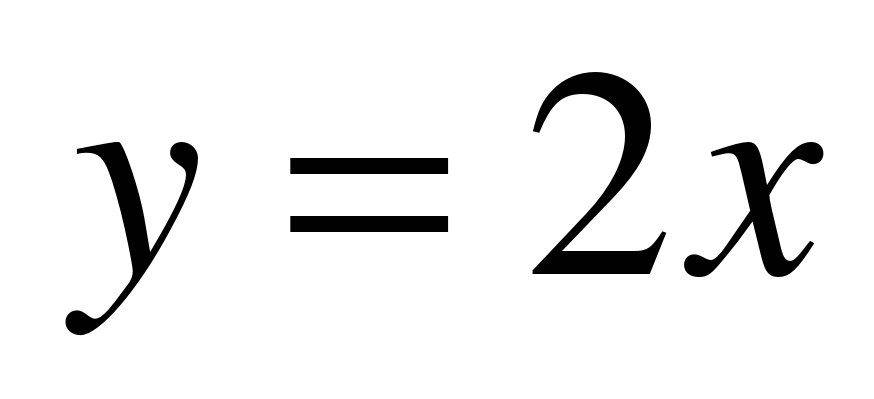
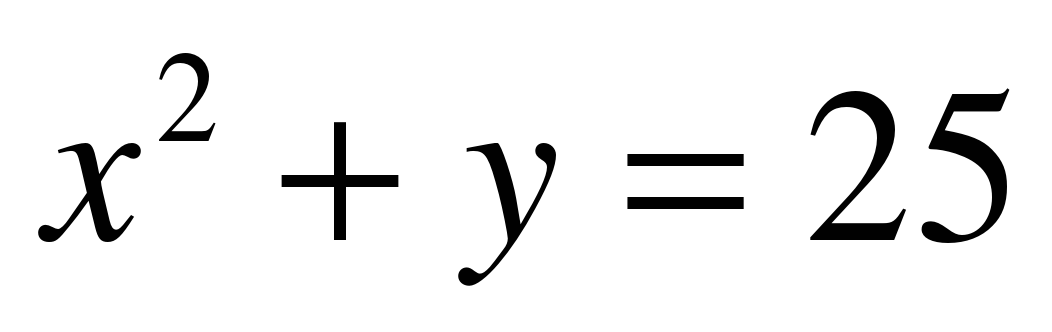
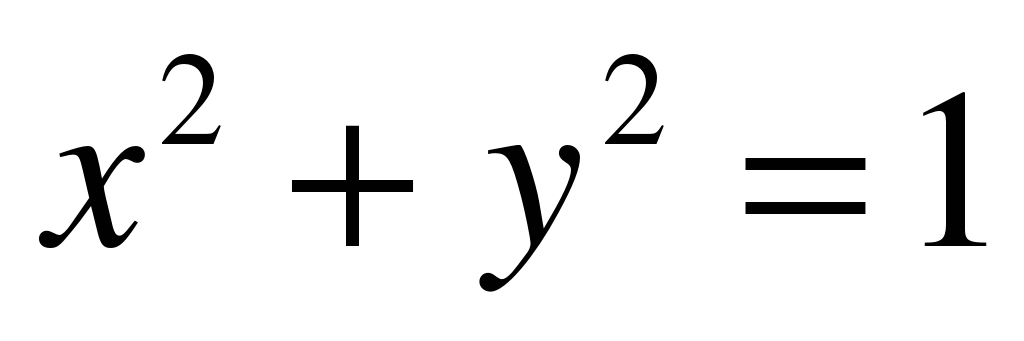
Среди формул а) ; б) ; в) найти такую, которая задает функцию.

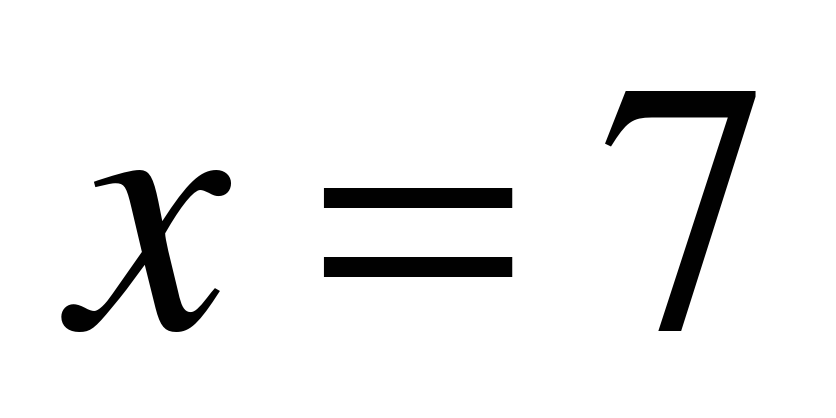
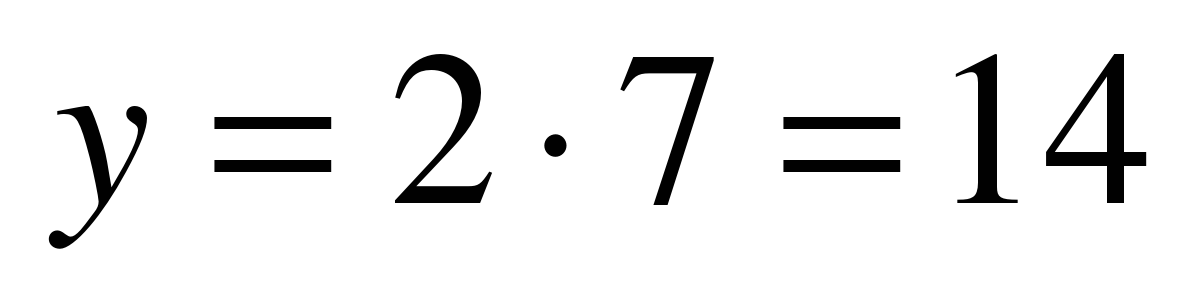
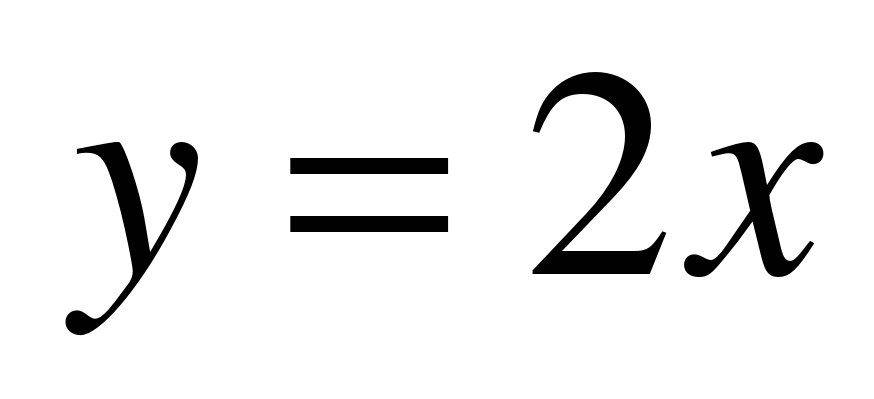
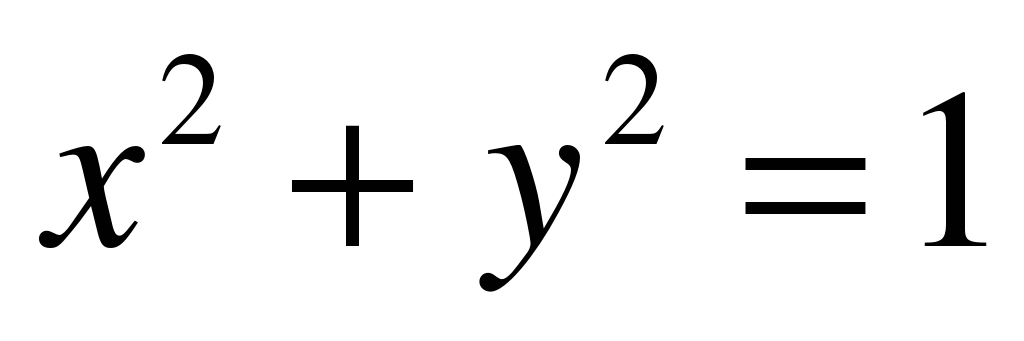
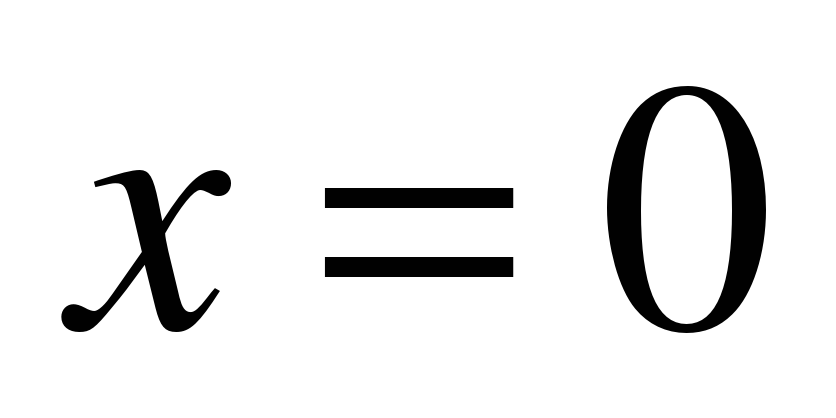
Решение: а, б) Для любого значения х по данной формуле значение у находится единственным образом, например, при получим, что , значит – формула, задающая функцию у от х. в) Формула не задает функцию, так как, например, значению , можно найти два соответствующих значения у: 1 и -1.

Изучение нового материала

Рассмотрим понятие функции более широко.

В своей практической деятельности человек сталкивается с величинами различной природы: длина, площадь, объем, масса, температура, вес и т.д.

В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т.е. не меняются; другие наоборот, принимают различные значения.

Все величины, изучаемые в математике, делятся на постоянные и переменные. (Формулируются соответствующие определения)

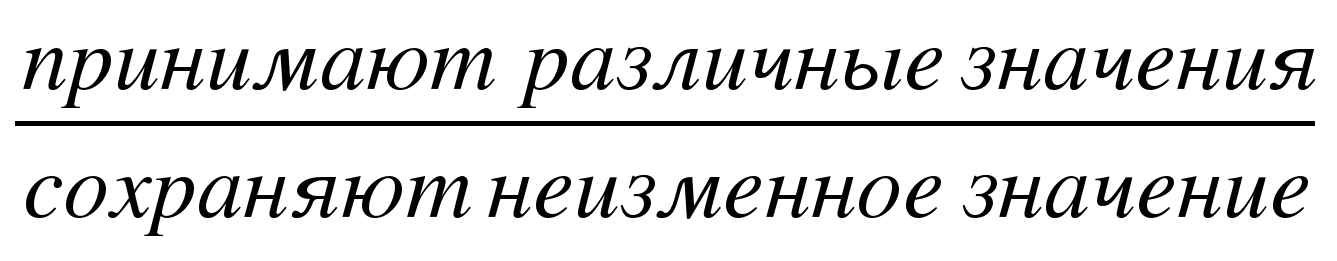
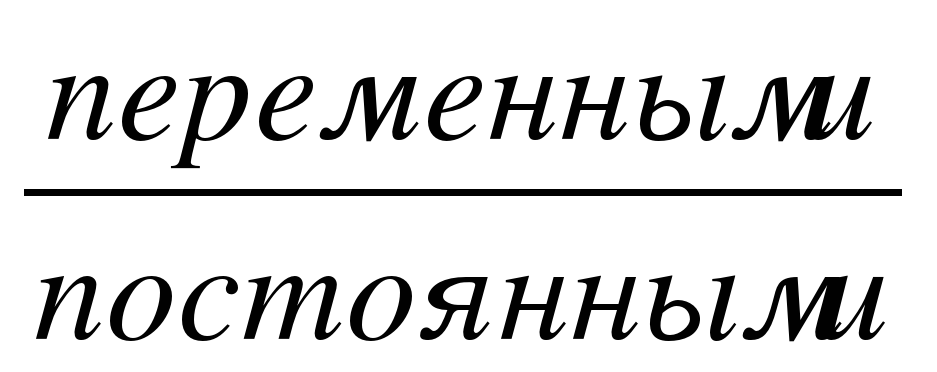
Те из величин, которые в рассматриваемом процессе называются величинами.

Определение. Правило, или закономерность, при котором каждому значению х из множества Х соответствует единственное значение у из множества Y, называется функцией. Обозначение: .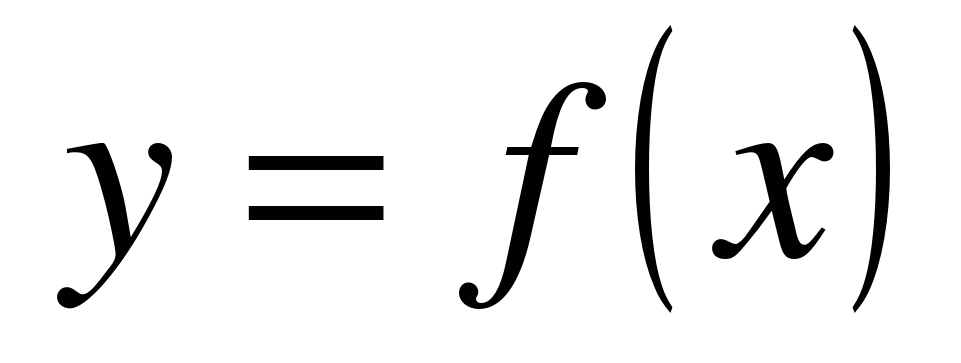

Уточним смысл некоторых понятий, известных вам из курса алгебры 7-9 класса. (Ученики формулируют, учитель при необходимости корректирует. Формулировки выводятся на экран.)

Источник