Урок математики в 5 классе «Арифметические способы решения текстовых задач»
Урок математики в 5 классе «Арифметические способы решения текстовых задач»
Дистанционное обучение педагогов по ФГОС по низким ценам
Вебинары, курсы повышения квалификации, профессиональная переподготовка и профессиональное обучение. Низкие цены. Более 13500 образовательных программ. Диплом госудаственного образца для курсов, переподготовки и профобучения. Сертификат за участие в вебинарах. Бесплатные вебинары. Лицензия.
Урок математики в 5 классе
«Арифметические способы решения текстовых задач»
Солдатова Светлана Анатольевна
учитель математики первой категории
МОУ Угличский физико-математический лицей
Образовательная: повторить, обобщить и систематизировать приёмы решения текстовых задач арифметическим способом.
Воспитательная: формировать личностные качества: сосредоточенность и внимание; настойчивость в достижение цели.
Развивающая: развивать познавательные интересы в процессе решения нестандартных задач, умения владеть математической терминологией, правильно и четко выражать мысль.
. Организационный момент.
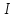
— Сегодня на уроке мы будем решать задачи. Они будут различны по типу, но объединять их будет то, что для решения будет отдано предпочтение арифметическому способу. А так как тема предыдущего урока –«Среднее арифметическое», то на уроке будут разобраны задачи на эту тему.
. Устный упражнения:
– Несколько задач я предлагаю вам решить устно, т.к. для их решения не требуется сложных вычислений, а способы решения вам уже знакомы.
а) (Задача-шутка) Шёл старик в Москву, повстречал 7 старушек: у каждой из них было по мешку, а в каждом мешке по коту. Сколько существ направлялось в Москву?
б) (Старинная индийская задача) Из четырёх пожертвователей второй дал вдвое больше первого, третий – втрое больше второго, а четвёртый — вчетверо больше третьего, а все вместе дали 132 монеты. Сколько монет дал первый?
132 монеты (на доске краткая запись задачи)
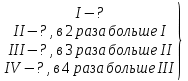
— Что удобно принять за 1 часть?
— Сколько всего монет частей приходится на 132 монеты? (1+2+6+24=33)
132:33=4 (м) – у первого жертвователя.
в) У Олега и Димы вместе72 марки. Сколько марок у каждого, если у Олега на 6 марок меньше?
— Определите тип задачи. (Нахождение двух чисел по их сумме и разности)
— Назовите все возможные способы решения данной задачи.
1способ: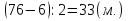 
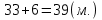
– у Олега.
— у Димы.
(используется понятие «удвоенное меньшее число»)
2 способ: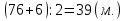 
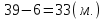
— у Димы.
— у Олега.
(используется понятие «удвоенное большее число»)
3 способ: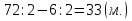 
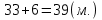
— у Олега.
— у Димы.
(используются понятия «полусумма» и «полуразность», так называемый «старинный способ»)
Решение задач по теме «Среднее арифметическое».
а) Настя и Ксюша поделили грибы поровну. У каждой стало по 22 гриба. Сколько грибов набрала каждая, если первоначально у Насти было на 8 грибов больше?
— Какие способы решения вы предлагаете?
— Какой способ самый рациональный по вашему мнению? (среднее арифметическое – это полусумма для двух чисел).
1) 
(г.) — полуразность.
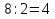
Ответ: 26 грибов, 18 грибов.
б) Среднее арифметическое трёх чисел 0,43. Первое число в 1,5 раза больше второго, а третье в 1,8 раза больше второго. Найдите первое число.
1) 
(г.) – приходится на сумму трёх чисел.
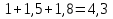
2) 
– 
число.
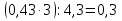
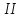
3) 
– 
число.
. Задачи на «предположение»
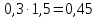
а) (Старинная китайская задача). В клетке находятся 35 фазанов и кроликов. Известно, что у них 94 ноги. Узнайте число фазанов и число кроликов.
— Предположим, что в клетке сидели бы только фазаны. Сколько ног имели бы 35 фазанов? (дети записывают решение в тетради, а учитель на доске)
1) 2 
35=70(н.) – если бы было 35 фазанов
— Почему ног больше? (Среди них есть кролики, у которых 4 ноги).
— Если мы одного фазана заменим на кролика, на сколько увеличится количество ног?
2) 4-2=2(н) — на столько ног больше у одного кролика, чем у одного фазана.
— А на сколько ног всего больше?
3) 94-70=24(н.) на столько всего больше ног.
Как узнать количество кроликов?
4) 24:2=12 — кроликов.
5) 35-12=23 – фазанов.
Ответ: 12 кроликов, 23 фазана.
-Есть очень интересное рассуждение, найденное в старых источниках. Представьте, что на верх клетки, в которой сидят фазаны и кролики, мы положим морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки.
— Сколько ног в этот момент будут стоять на земле?
— А где остальные?
— Сколько же кроликов?
— Сравните наше рассуждение с записью решения в тетради.
— А теперь попробуйте самостоятельно решить следующую задачу.
б) В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе
19 голов и 46 ног?
30 голов и 74 ноги? (по вариантам, 2 человека у доски с последующей проверкой)
1)2 19=38(н.) – если бы все были куры.
2) 46-38=8(н) — на столько ног больше.
Ответ: 4 овцы, 15 кур.
1)2 30=60(н.) – если бы все были куры.
2) 74-60=14(н) — на столько ног больше.
Ответ: 7 овец, 23 куры.
1) (г.) – приходится на сумму трёх чисел.
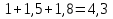
2) – число.
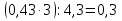
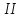
3) – число.
. Разные задачи (старинные)
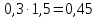
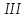
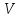
а) Лошадь вместе с седлом стоит 235 р., лошадь вместе со сбруей стоит 250 р., сбруя вместе с седлом стоит 135 р. Сколько стоит лошадь, сколько сбруя и сколько седло?
1) 250+235+135=620(р.) — стоят 2 лошади, 2 сбруи и 2 седла.
2) 620:2 =310(р.) – стоит лошадь, седло и сбруя.
3) 310-235=75(р.) – стоит сбруя.
4) 250-75=175(р.) – стоит лошадь.
5) 235-175=60(р.) – стоит седло.
Ответ: 175 р., 75.р., 60 р.
б ) Крестьянин хочет купить лошадь и для этого продаёт рожь. Если он продаст 15 ц ржи, то ему не хватит для покупки лошади 80 р., а если он продаст 20 ц ржи, то у него останется 110 р. Сколько стоит лошадь?
2) 80 +110=190(ц) стоят 5ц ржи.
3)190:5=38(р.) стоит 1ц ржи.
4) 38 20-110=650(р.) – стоит лошадь.
. Подведение итогов.
Домашнее задание.
1) На лугу паслось несколько коров. У них ног на 24 больше, чем голов. Сколько коров паслось на лугу ?
2) Старинная задача. За 1000 р. Я купил 44 коровы – по 18 р. и по 26 р. Сколько тех и других?
Шевкин А. В. Обучение решению текстовых задач в 5-6 классах. – М.: Галс плюс,1998.
Источник
Разработка урока по теме «Арифметические способы решения текстовых задач. Задачи на части.»
Урок математики в 5-м классе:
«Арифметические способы решения текстовых задач»
«Задачи на части»
Фенько Евгения Александровна, учитель математики
УМК: компоненты УМК «Сферы. Математика 5»
Личностные : проявлять внимание и интерес к учебному процессу, уметь анализировать, оценивать ситуацию, выражать доброжелательное отношение к познанию, оценивать собственную учебную деятельность, проявлять самостоятельность, инициативу, ответственность, сравнивать разные точки зрения, считаться с мнением другого, уметь работать в парах и группах, слушать собеседника и вести диалог, аргументировать свою точку зрения.
Метапредметные : умение применять и сохранять учебную задачу, планировать решение задачи, вносить изменения в процесс, намечать способы устранения ошибок, осуществлять итоговый контроль, обрабатывать информацию, записывать ее и воспринимать; использовать модели, знаки, символы и схемы; осуществлять логические операции; выбирать способы решения задач в зависимости от конкретных условий; формировать умение сотрудничать с учителем и сверстниками при решении учебной задачи, принимать на себя ответственность за результат своих и коллективных действий, оформлять диалогическое высказывание в соответствии с требованиями речевого этикета; формировать умение слушать и вступать в диалог; формировать внимательность и аккуратность в вычислениях; воспитывать чувство взаимопомощи, культуру учебного труда, требовательное отношение к себе и к своей работе.
Предметные : освоение систематических знаний, их преобразование, применение и самостоятельное пополнение, владение представлениями о типах задач и методах их решения, умение в процессе реальной ситуации использовать эти знания и умения.
Образовательная — расширить представление учащихся о свойствах арифметических действий, отработать умения решать задачи на части арифметическим способом.
Развивающая – обучать приемам и методам рассуждения, развивать логическое мышление учащихся, математическую речь (устную и письменную), внимание.
Воспитательная — развивать интеллектуальные и творческие способности учащихся, познавательную активность, интерес к математике.
Показать знания, полученные по теме “Задачи на “части” и продемонстрировать их практическую значимость.
Тип урока: урок повторения изученного материала.
Форма урока: комбинированный урок
Продолжительность урока: 45 минут
Оборудование урока: наглядность по теме урока, классная доска, распечатки индивидуального мини-проектного задания на дом, рабочие тетради, линейка, карандаш.
I. Организационный момент (Целеполагание, саморегуляция)
II. Актуализация опорных знаний
III. Решение простейших задач на части
IV. Практическая часть
V. Применение знаний
VI. Подведение итогов урока
VII. Домашнее задание
I. Организационный момент
Здравствуйте, ребята. Садитесь. Разгадайте шараду и вы узнаете, чем мы будем сегодня заниматься на уроке:
Первое — предлог, второе – летний дом, а целое порой решается с трудом! (Задача)
Сегодня у нас урок закрепления по теме “ Арифметические способы решения текстовых задач на части ”.
II. Актуализация знаний.
Прежде мы приступим к работе по теме урока, я бы хотела проверить как вы справились с домашним заданием. Есть ли вопросы по домашнему заданию? Откройте ваши тетради, я пройду, посмотрю ваши работы.
А теперь повторим пройденный материал.
Заполнить таблички из раздаточного материала.
Источник
