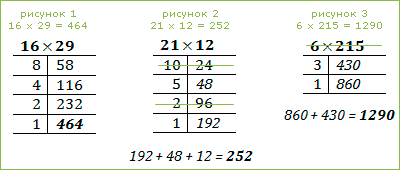Таблица умножения по китайскому способу

СПОСОБЫ УМНОЖЕНИЯ БЕЗ ТАБЛИЦЫ УМНОЖЕНИЯ (гимнастика для ума)

Предлагаю читателям зелёных страничек два способа умножения, в которых не используется таблица умножения 😉 Надеюсь, что этот материал придётся по душе преподавателям информатики, который они могут использовать при проведении факультативных занятий.

Русский способ умножения

Способ этот, был употребителен в обиходе русских крестьян и унаследован ими от глубокой древности. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа, таблица умножения в этом деле без надобности 🙂

Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и даёт искомый результат (рисунок 1). Нетрудно понять, на чём этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение.

Однако как поступить, если при этом приходится делить пополам нечётное число? В этом случае от нечётного числа откидываем единицу и делим остаток пополам, при этом к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет искомым произведением (рисунки: 2, 3).
Иными словами все строки с чётными левыми числами зачёркиваем; оставляем, а затем суммируем не зачёркнутые числа правого столбца.

Для рисунка 2: 192 + 48 + 12 = 252
Правильность приёма станет ясна, если принять во внимание, что:
5 × 48 = (4 + 1) × 48 = 4 × 48 + 48
21 × 12 = (20 + 1) × 12 = 20 × 12 + 12
Ясно, что числа 48, 12, утрачиваемые при делении нечётного числа пополам, необходимо прибавить к результату последнего умножения, чтобы получить произведение.
Русский способ умножения и элегантен и экстравагантен одновременно 😉

§ Логическая задачка о Змее Горыныче и прославленных русских богатырях на зелёной страничке «Кто из богатырей победил Змея Горыныча?»
решение логических задач средствами алгебры логики
Для тех, кто любит учиться! Для тех, кому в радость гимнастика для ума 😉
§ Решение логических задач табличным способом

Китайский. Рисовательный способ умножения

С этим способом умножения меня познакомил сын, предоставив в моё распоряжение несколько листочков из блокнота с готовыми решениями в виде замысловатых рисунков. Закипел процесс расшифровки алгоритма рисовательного способа умножения 🙂 Для наглядности решила прибегнуть к помощи цветных карандашей, и… лёд тронулся господа присяжные 🙂
Предлагаю Вашему вниманию три примера в цветных картинках (в правом верхнем углу проверочный столбик).

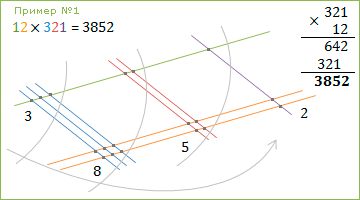
Пример №1 : 12 × 321 = 3852
Рисуем первое число сверху вниз, слева на право: одна зелёненькая палочка (1); две оранжевых палочки (2). 12 нарисовали 🙂
Рисуем второе число снизу вверх, слева на право: три голубеньких палочки (3); две красненькие (2); одну сиреневенькую (1). 321 нарисовали 🙂

Теперь простым карандашиком по рисунку прогуляемся, точечки пересечения чисел-палочек на части разделим и приступим к подсчёту точечек. Двигаемся справа налево (по часовой стрелке): 2, 5, 8, 3. Число-результат будем «собирать» слева направо (против часовой стрелки) и… вуаля, получили 3852 🙂

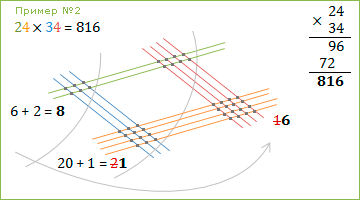
Пример №2 : 24 × 34 = 816
В этом примере есть нюансы 😉 При подсчёте точечек в первой части получилось 16. Единичку отправляем-прибавляем к точечкам второй части (20 + 1)…

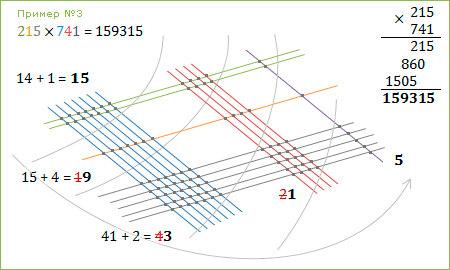
Пример №3 : 215 × 741 = 159315
Без комментариев 🙂

На первых порах рисовательный способ умножения показался мне несколько вычурным, но при этом интригующим и удивительно гармоничным. На пятом примере поймала себя на мысли, что умножение идёт в лёт 🙂 и работает в режиме автопилота: рисуем, точечки считаем, про таблицу умножения не вспоминаем, вроде как мы её вообще не знаем :-)))

Если честно, то осуществляя проверку рисовательного способа умножения и обратившись к умножению столбиком, и не раз, и не два к своему стыду отметила некоторые притормаживания, свидетельствовавшие о том, что таблица умножения у меня проржавела в некоторых местах 🙁 и забывать её таки не стоит. При работе с более «серьёзными» числами рисовательный способ умножения стал чересчур громоздким, а умножение столбиком пошло в радость.

§ Ещё один эскиз тыльной стороны блокнота с календариком на 2012 год смотрите на зелёной страничке «Блокнот: Для вашего творчества – KurskOnline».

P.S.: Слава и хвала родному советскому столбику!
В плане построения способ непритязательный и компактный, очень даже скоростной, память тренирует – таблицу умножения забывать не дозволяет 🙂 И посему, настоятельно рекомендую и себе и Вам по возможности забывать про калькуляторы в телефонах и на компьютерах 😉 и периодически баловать себя умножением столбиком. А то не ровен час и сюжет из фильма «Восстание машин» развернётся не на экране кинотеатра, а на нашей с Вами кухне или лужайке рядом с домом…
Три раза через левое плечо…, стучим по дереву… :-))) …и главное не забываем про гимнастику для ума!

Для любознательных : Умножение обозначается знаком [ × ] или [ · ]
Знак [ × ] ввёл английский математик Уильям Оутред в 1631 году.
Знак [ · ] ввёл немецкий учёный Готфрид Вильгельм Лейбниц в 1698 году.
В буквенном обозначении эти знаки упускаются и вместо a × b или a · b пишут ab.

В копилочку веб-мастера : Некоторые математические символы на HTML

°	° или °	градус
±	± или ±	плюс-минус
¼	¼ или ¼	дробь – одна четверть
½	½ или ½	дробь – одна вторая
¾	¾ или ¾	дробь – три четверти
×	× или ×	знак умножения
÷	÷ или ÷	знак деления
ƒ	ƒ или ƒ	знак функции
′	′ или ′	одиночный штрих – минуты и футы
″	″ или ″	двойной штрих – секунды и дюймы
≈	≈ или ≈	знак примерного равенства
≠	≠ или ≠	знак не равно
≡	≡ или ≡	тождественно
>	> или >	больше
или или ≥	больше или равно
≤	≤ или ≤	меньше или равно
∑	∑ или ∑	знак суммирования
√	√ или √	квадратный корень (радикал)
∞	∞ или ∞	бесконечность
Ø	Ø или Ø	диаметр
∠	∠ или ∠	угол
⊥	⊥ или ⊥	перпендикулярно

§ Греческий алфавит на HTML с указанием произношения букв
для тех, кто вращается на орбитах астрономии, математики, физики 😉

Источник

Китайская таблица умножения — Chinese multiplication table

Китайская таблица умножения является первым условием для использования исчисления Rod для проведения умножения, деления, извлечения квадратного корня, и решения уравнений на основе значения места десятичной системы счисления. Он был известен в Китае еще в весенний и осенний период и пережил век абака ; ученики начальной школы сегодня все еще должны запоминать его.

Китайская таблица умножения состоит из восьмидесяти одного члена. Его часто называли таблицей девять-девять или просто девять-девять , потому что в древние времена таблица девять-девять начиналась с 9 × 9: девять девяток порождают восемьдесят один, восемь девяток порождают семьдесят два . семь девяток порождают шестьдесят три и т. д. два рождают одного. По мнению Ван Гоуэя , известного ученого, таблица девять-девять, вероятно, начиналась с девяти из-за «поклонения девяти» в древнем Китае; Император считался «девяти пятью превосходством» в Книге Перемен . См. Также « Числа в китайской культуре № Девять» .

Она также известна как песня (или стихотворение) девять-девять , поскольку таблица состоит из восьмидесяти одной строки с четырьмя или пятью китайскими иероглифами в каждой; таким образом, был создан постоянный метр и таблица умножения превратилась в стихотворение. Например, 9×9 = 81 будет отображаться как «九九 八十 一» или «девять девять восемьдесят один» с подразумеваемым миром для «порождает» «得». Это позволяет легко выучить наизусть. Более короткая версия таблицы состоит всего из сорока пяти предложений, так как такие термины, как «девять восьмерок порождают семьдесят два», идентичны «восемь девяток порождают семьдесят два», поэтому нет необходимости заучивать их дважды. Когда в династии Мин счеты заменили счетные стержни, многие авторы по счетам выступали за использование полной таблицы вместо более короткой. Они утверждали, что запоминание этого без необходимости вдуматься значительно ускоряет вычисления.

Существование китайской таблицы умножения свидетельствует о ранней позиционной десятичной системе: в противном случае потребовалась бы гораздо большая таблица умножения с членами, превышающими 9 × 9.

СОДЕРЖАНИЕ

Текст песни Nine-nine на китайском языке

九九乘法 口诀 表
一一 得 一
一二 得 二 二 二
一 三 得 三 二三 得 六 三 得 九
一 四 得 四 二四 得 三四 十二 四 四 十六
一 五 得 五 二十三五五一十五四五二十五五二十五
一六得六二六十二三六十八四六二十四五六三十六六三十六
一七得七二七十四二十一三七四七二十八五七三十五六七四十二七七四十九
一八得八二八十六三八二十四四八三十二五八四十六八四十八 七八 五 十六 八八 六十 四
二 十七 四九 三 十六 五 九四 九五 十四 七九 三 八九 七 十二九九 八十 一

Его можно читать как по строкам, так и по столбцам.

Таблица девяти девяти в китайской литературе

Многие китайские классики ссылаются на таблицу девять-девять:

• Чжуби Суаньцзин : «девять девять восемьдесят один»
• В Гуань Цзы есть предложения вида «три восьмерки порождают двадцать четыре, три семерки порождают двадцать одно».
• Девять глав о математическом искусстве : « Фу Си изобрел искусство девять-девять».
• В Хуайнаньцзы было восемь предложений: «девять девяток рождают восемьдесят одно», «восемь девяток рождают семьдесят два», вплоть до «две девятки порождают восемнадцать».
• В Дунь Хуане была обнаружена рукопись с девятью девятью таблицами .
• Вычислительные каноны Ся Хоуяна : «Чтобы научиться искусству умножения и деления, нужно понимать девять-девять».
• Автор династии Сун в «Записных книжках» Хун Чжай сказал: «три тройки как девять, три четверки как двенадцать, две восьмерки как шестнадцать, четыре четверки как шестнадцать, три девятки как двадцать семь, четыре девятки как тридцать шесть, шесть шестерок как тридцать шесть, пять восьмерок». как сорок, пять девяток как сорок пять, семь девяток как шестьдесят три, восемь девяток как семьдесят два, девять девяток как восемьдесят один «. Это говорит о том, что таблица началась с наименьшего срока со времен династии Сун.
• Учебник математики математика династии СунЯн Хуэй : Суан фа тонг бянь бен мо , что означает: «Вы должны выучить девять девять песен из одной, равной от одной до девяти девяти восьмидесяти, в порядке от малого до большого».
• Династии Юань математик Чжу Шицзе «s Suanxue qimeng (Элементарная математика):«один один равняется один, два на два равно четыре, один на три равно три, два на три равно шесть, три на три равно девять, один на четыре равно четыре. .. девять на девять равно восемь один «

Источник

Обмен опытом

Суть китайско-японского метода

Суть китайского метода состоит в визуализации произведения с помощью графического изображения процесса умножения. Другими словами, числа изображаются в виде прямых линий, сотни, десятки и единицы отделяются промежутками и располагаются параллельно друг другу на плоскости. Один из множителей располагается горизонтально сверху вниз, второй — вертикально слева направо. Количество пересечения линий, образующих десятки при умножении двузначных чисел, будет первой цифрой в произведении. Точки пересечения десятков и единиц — вторая цифра результата, количество точек, образовавшихся при пересечении всех единиц — третья цифра.

Перемножим два двузначных числа: 13*12=156

Шаг 1 Горизонтально рисуем линии первого числа 13:
Единицу – одной линией. Тройку – чуть ниже тремя параллельными линиями

Шаг 2 Вертикальными линиями слева направо рисуем второе число 12:
Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями

Шаг 3 Подсчитываем количество точек в трех группах:
Левый верхний угол – 1 (Сотни)
Правый верхний и левый нижний углы (Диагональ) – 5 (Десятки)
Правый нижний угол – 6 (Единицы)

Шаг 4 Подсчитываем результат:

Перемножим два двузначных числа: 15*23=345

Источник

Древнейшая таблица умножения на бамбуке из Китая

Китайские историки заявляют, что ими восстановлена самая древняя в мире таблица умножения, в основании которой — число 10. Древнейшая таблица умножения на бамбуке из Китая поразила исследователей уровнем познаний древних китайцев.

Учёные в Китае выровняли фрагменты бамбука, с нанесёнными на них китайскими каллиграфическими записями, чтобы воссоздать математический документ. Он использовался 2300 лет назад, что делает его старейшей в мире известной десятичной таблицей умножения.

В 2008 году исследователи из Университета Цинхуа в Пекине получили в дар почти 2500 ветхих бамбуковых полосок от человека, который купил их на рынке в Гонконге. Они датируются примерно 305 годом до нашей эры от периода Сражающихся царств до объединения Китая во времена династии Цинь.

Как устроена древнейшая таблица умножения

Каждая полоска была около 7 — 13 мм в ширину и до примерно 50 см. в длину, с вертикальной линией каллиграфии, написанной черными чернилами.

Однака 21-я полоска отличалась от других. На ней были только цифры. При правильном расположении они образовывали матричную структуру. Верхний ряд и правый столбец содержат 19 цифр, расположенных справа налево и сверху вниз соответственно: 0,5, затем целые от 1 до 9, за ними кратные 10 — от 10 до 90.

«Все полоски перемешались, так как нити, которыми были связаны манускрипты в единый свиток давно истлели» — сказал палеограф Ли Цзюньмин (Li Junming) журналу Nature. Это было «как собирание головоломки», потому что некоторые части были сломаны, а другие пропали. «Это действительно древний калькулятор».

Как и в знакомой нам современной таблице умножения, запись на пересечении ряда и столбца показывает результат умножения. С помощью древней таблицы можно умножить любое целое или половину целого числа от 0,5 до 99,5.

Использование таблицы умножения в древнем Китае

По мнению учёных, древнейшая таблица умножения могла использоваться чиновниками для расчёта площади поверхности земли, урожайности культур и налогов. С помощью таблицы можно даже вычислять квадратные корни.

Однако исследователи не уверены, что такие сложные математические действия применялись людьми того времени, считает Фэн Лишэн (Feng Lisheng), доктор математических наук.

«Такая сложная матрица умножения абсолютно уникальна в истории Китая», — добавил он.

До настоящего времени самыми старейшими считали китайские таблицы умножения периода правления династии Цинь (221 — 206 гг. до н.э). Обнаруженная древнейшая таблица умножения на бамбуке — это бесценное наследие древнего Китая, в очередной раз поразило глубиной и мудростью жителей Поднебесной империи тех далеких времен.

Источник