Табличный способ закон распределения

Основные законы распределения

Главная Репетиторы Учебные материалы Контакты

В таблице m — число заказов, полученных компанией на покупку телевизора. С_n m — число сочетаний m телевизоров по n, p — вероятность наступления события А, т.е. заказа телевизора, q — вероятность не наступления события А, т.е. не заказа телевизора, P m,n — вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей.

2.Геометрическое распределение.

Геометрическое распределение случайной величины имеет следующий вид:

P m — вероятность наступления события А в испытание под номером m.
р — вероятность наступления события А в одном испытании.
q = 1 — p

Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.

Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 — что десятый блок оказался неисправным — 0,038742049 , 2 — что все проверяемые блоки оказались исправными — 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события P m (10 проверенных блоков) относительно высокая. Рис.2.

3.Гипергеометрическое распределение.

Гипергеометрическое распределение случайной величины имеет следующий вид:

Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M — всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m — число правильно угаданных чисел среди изъятых.

Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.

4.Закон распределения Пуассона.

Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:

λ = np = const
n — число испытаний, стремящиеся к бесконечности
p — вероятность наступления события, стремящаяся к нулю
m — число появлений события А

Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B — 0,06 и C — 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей.

Из условия имеем: m=100, λ 1 =8, λ 2 =6, λ 3 =4 ( ≤10 )

(таблица дана не полностью)

Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)

Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.

5.Равномерный закон распределения.

Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.

6.Нормальный закон распределения (закон Гаусса).

Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:

где
а — математическое ожидание случайной величины
σ — среднее квадратическое отклонение

График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:

При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.

Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:

Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть — от а до х. (Рис.7)

7.Показательный закон распределения.

Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид:

где λ — параметр обратно-пропорциональный математическому ожиданию.

График плотности вероятности с параметрами
λ = 2, λ = 4, λ =6 изображен на рис.8

Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид:

График функции изображен на рис.9

Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:

8.Логарифмически-нормальное распределение.

Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид.

Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)

9. χ ² распределение

Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением.

χ ² распределение имеет вид:

А i — i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3. k).

Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:

Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.

10.Распределение Стьюдента (t — распределение)

Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид:

Z — случайная величина, распределенная по нормальному закону.
χ ² — случайная величина, имеющая χ ² — распределение с k степенями свободы.

Плотность вероятности распределения Стьюдента имеет вид:

На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.

11. Распределение Фишера-Снедекора.

Распределение случайной величины Фишера-Снедекора имеет вид:

Плотность вероятности случайной величины имеет вид:

При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)

Источник

Формулы: законы распределения случайных величин

В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.

Каталог формул по теории вероятности онлайн

Законы распределения на этой странице

Дискретные случайные величины

Биномиальное распределение ДСВ

Пусть дискретная случайная величина $X$ — количество «успехов» в последовательности из $n$ независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна $p$ («неуспеха» — $q=1-p$).

Закон распределения $X$ имеет вид:

Главная > Учебные материалы > Математика: Основные законы распределения 1.Биномиальный закон распределения. 2.Геометрическое распределение. 3.Гипергеометрическое распределение. 4.Закон распределения Пуассона. 5.Равномерный закон распределения. 6.Нормальный закон распределения (закон Гаусса). 7.Показательный закон распределения. 8.Логарифмически-нормальное распределение. 9. χ ² распределение. 10.Распределение Стьюдента (t — распределение). 11.Распределение Фишера-Снедекора. 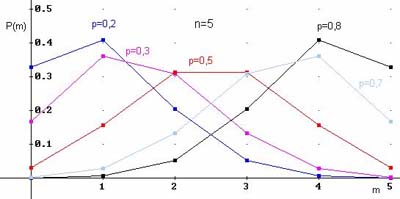1.Биномиальный закон распределения. Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна. Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.
	Рис.1
	Рис.2
	Рис.3
	Рис.10

$x_k$	0	1	.	k	.	n
$p_k$	$q^n$	$n\cdot p \cdot q^$	$C_n^k \cdot p^k \cdot q^$	$p^n$

Здесь вероятности находятся по формуле Бернулли:

$$ P(X=k) = C_n^k \cdot p^k \cdot (1-p)^ = C_n^k \cdot p^k \cdot q^, k=0,1,2. n. $$

Числовые характеристики биномиального распределения:

Примеры многоугольников распределения для $n=5$ и различных вероятностей:

Пуассоновское распределение ДСВ

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии $p\to 0$, $n \to \infty$, $np \to \lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения по закону Пуассона имеет вид:

$x_k$	0	1	.	k	.
$p_k$	$e^<-\lambda>$	$\lambda e^<-\lambda>$	.	$\frac<\lambda^k>\cdot e^<-\lambda>$	.

Вероятности вычисляются по формуле Пуассона:

Числовые характеристики для распределения Пуассона:

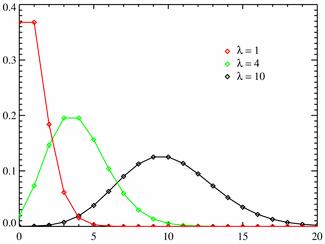
Разные многоугольники распределения при $\lambda = 1; 4; 10$.

Геометрическое распределение ДСВ

Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ — количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.

Формула для вероятностей:

$$ P(X=k) = q^k \cdot p, k=0,1,2. n. $$

Ряд распределения геометрического закона:

$x_k$	0	1	2	.	k	.
$p_k$	$p$	$q\cdot p$	$q^2 \cdot p$	.	$q^k \cdot p$	.

Гипергеометрическое распределение ДСВ

Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n \le N$). Найти закон распределения случайной величины $X$ — равной числу белых шаров среди выбранных.

Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n \lt K$, то до $n$). Вероятности вычисляются по формуле: $$ P(X=k)=\frac^>, \quad 0\le k \le K. $$

$$M(X)=\frac\cdot n, \quad D(X)=\frac\cdot n \cdot \frac \cdot \frac.$$

Непрерывные случайные величины

Показательное распределение НСВ

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Плотность распределения величины $X$(везде $ \lambda \gt 0)$:

Функция распределения величины $X$:

Числовые характеристики можно найти по формулам:

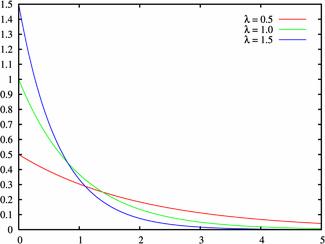
Плотность распределения при различных значениях $\lambda \gt 0$:

Равномерное распределение НСВ

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.

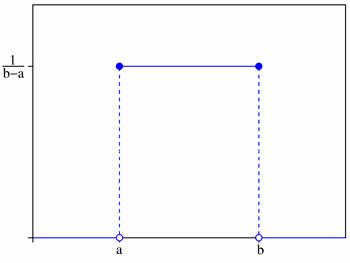
Плотность распределения на отрезке $(a;b)$:

$$ f(x)= \left\< \begin 0,\ x \le a\\ \frac <1>,\ a \lt x \le b, \\ 0,\ x \gt b, \\ \end \right. $$

$$ F(x)= \left\< \begin 0,\ x \le a\\ \frac ,\ a \lt x \le b, \\ 1,\ x \gt b, \\ \end \right. $$

Числовые характеристики равномерно распределенной случайной величины:

График плотности вероятностей:

Нормальное распределение или распределение Гаусса НСВ

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.

Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения нормальной случайной величины $X$ имеет вид:

При $a=0$ и $\sigma=1$ эта функция принимает вид:

Числовые характеристики для нормального распределения:

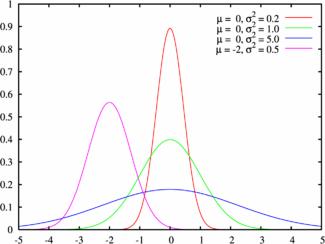
Пример графика плотности распределения для различных значений среднего и СКО:

Нормальный закон распределения случайной величины с параметрами $a=0$ и $\sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.

Функция Лапласа определяется как:

Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(\alpha, \beta)$:

$$ P(\alpha \lt X \lt \beta) = \Phi\left( \frac<\beta-a> <\sigma>\right) — \Phi\left( \frac<\alpha-a> <\sigma>\right). $$

Вероятность отклонения нормально распределенной случайной величины $X$ на величину $\delta$ от математического ожидания (по модулю).

Решенные задачи по теории вероятностей

Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:

Источник