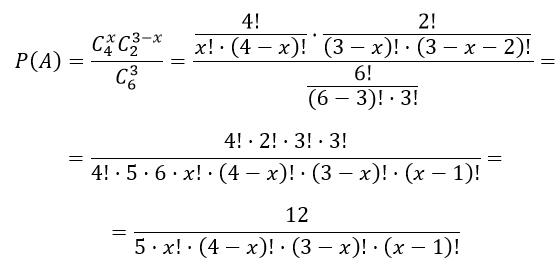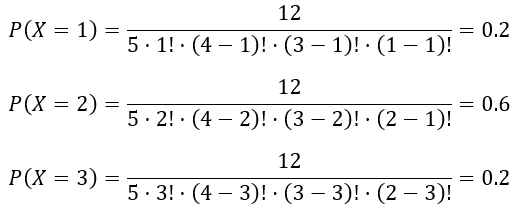Табличный способ задания закона распределения

Табличный способ задания закона распределения

Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.

Если для какой- либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение.

При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным.

Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам.

Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя.

Случайная величина связана со случайным событием.

Если случайное событие — качественная характеристика испытаний, то случайная величина — его количественная характеристика.

Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.

Источник

Закон распределения вероятностей дискретной случайной величины

Дата добавления: 2013-12-23 ; просмотров: 7586 ; Нарушение авторских прав

Определение2.1:Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Способы задания дискретной случайной величины

1) Для задания дискретной случайной величины достаточно задать семейство вероятностей p_i = P(X = x_i), где или .

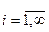
2) Табличный способ задания дискретной случайной величины: первая строка таблицы содержит возможные значения случайной величины, расположенные в порядке возрастания, а вторая – их вероятности:

X	x1	x2	x3	…..	xn
P	p1	p2	p3	…..	pn

Сумма вероятностей второй строки таблицы равна единице:

(условие нормировки).

Замечание1: В одном испытании случайная величина X принимает одно и только одно возможное значение, следовательно, события (X = x_i), где образуют полную группу.

Замечание2: Если множество возможных значений бесконечно (счетно), то ряд 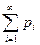сходится и его сумма равна единице.

3) Многоугольник распределения или графический способ задания дискретной случайной величины.

В прямоугольной системе координат строят точки ( x_i , p_i ), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

4) Задать закон распределения дискретной случайной величины можно в виде функции распределения вероятностей (интегральной функции распределения) F(x).

Пример.В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 10000 рублей и десять выигрышей по 1000 рублей. Найти ряд распределения, функцию распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета. Построить многоугольник распределения.

Решение: Случайная величина X принимает значения 0,1000,10000с вероятностями:

, , .Таким образом, ряд распределения имеет следующий вид:

X
P	0,89	0,1	0,01

Условие нормировки выполняется: .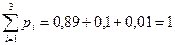

Источник

Урок: закон распределения дискретной случайной величины

Законом распределения дискретной случайной величины называется соответствие между возможными значениями и их вероятностями. Его можно задать таблично, графически и аналитически.

Что такое случайна величина разобрано в этом уроке.

При табличном способе задания первая строка таблицы содержит возможные значения, а вторая их вероятности, то есть

X	x1	x2	…	xi	…	xn
P	p1	p2	…	pi	…	pn

Такую величину называют рядом распределения дискретной случайной величины.

Х=х1, Х=х2, Х=хn образуют полную группу, так как в одном испытании случайная величина примет одно и только одно возможное значение. Следовательно, сумма их вероятностей равна единице, то есть p1 + p2 + pn = 1 или

Если множество значений Х бесконечно, тоПример 1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 1000 рублей и 10 по 100 рублей. Найти закон распределения случайной величины Х — стоимость возможного выигрыша для владельца одного лотерейного билета.

Искомый закон распределения имеет вид:

X	1000	100	0
P	0,01	0,1	0,89

Контроль; 0,01+0,1+0,89=1.
При графическом способе задания закона распределения на координатной плоскости строят точки (Xi:Pi), а затем соединяют их отрезками прямой. Полученную ломаную линию называют многоугольником распределения. Для примера 1 многоугольник распределения изображен на рисунке 1.

При аналитическом способе задания закона распределения указывают формулу, связывающую вероятности случайной величины с ее возможными значениями.

Примеры дискретных распределений

Биномиальное распределение

Пусть производится n испытаний, в каждом из которых событие А наступает с постоянной вероятностью p , следовательно, не наступает с постоянной вероятностью q = 1- p . Рассмотрим случайную величину X — число появления события A в этих n испытаниях. Возможными значениями X являются x1 = 0 , x2 = 1,…, xn+1 = n . Вероятность этих возможных

значений определяется по формуле Бернулли P (k) = Ck *pk qn-k .

Получили закон распределения

Этот закон распределения называется биномиальным.

Распределение Пуассона

Если решить предыдущую задачу при условии, что число испытаний n велико, а вероятность p появления события A в каждом испытании мала, то можно получить формулу

Эта формула выражает закон распределения Пуассона для массовых ( n велико) и редких (p мало) событий. Существуют таблицы для определения Pn (k) .

Источник

Закон распределения дискретной случайной величины

Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х₁, х₂,…,х_n этой величины и их вероятностями p₁, p₂,…,p_n

Может быть задан аналитически, графически или таблично.

Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть

X	x1	x2	……	xn
P	p1	p2	……	pn

х₁, х₂,…,х_n — значения дискретной случайной величины;
p₁, p₂,…,p_n — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p₁+p₂+ … +p_n=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли. Рассмотрим примеры

Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p₁(6)=6/10=0,6;
p₂(4)=4/10=0,4

X	6	4
P	0.6	0.4

Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x₁=4; x₂=6; x₃=8; x₁=2
Найдем их вероятности:

p₁(4)=4/20=0,2;
p₂(6)=6/20=0,3;
p₃(8)=8/20=0,4;
p₄(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины

X	4	6	8	2
P	0.2	0.3	0.4	0.1

Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение

n=5+13+7=26

Таблица имеет вид:

X	5	13	8	2
P	0.2	0.52	0.28	0.1

Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем: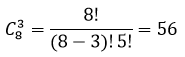

при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные.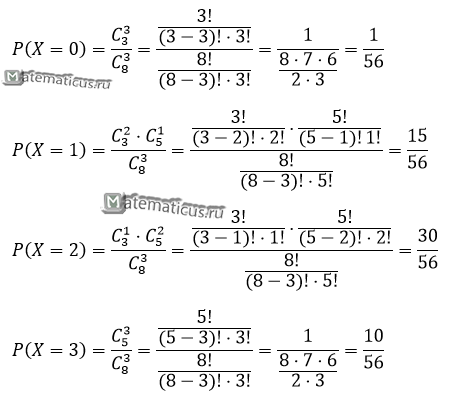

Составим таблицу распределения

X	0	1	2	3
P	0.018	0.268	0.536	0.178

Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.

Решение

Возможные варианты значений СВ X: 1, 2, 3

$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;

$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.

$C_2^<3 — x>$ — общее число способов отбора нестандартных деталей

Тогда вероятности события A вычисляются по формуле

Закон распределения дискретной случайной величины X для составления ряда распределения:

Получаем таблицу ряда распределения ДСВ

X	0	1	2	3
P	0	0.2	0.6	0.2

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.9 / 5. Количество оценок: 9

Источник