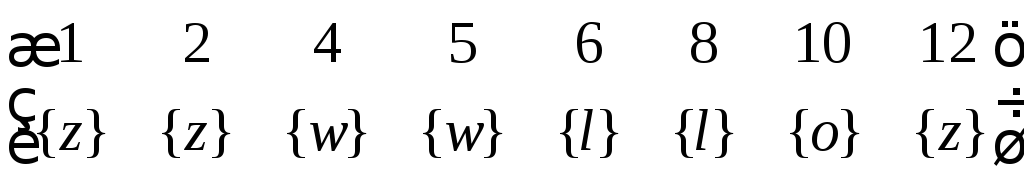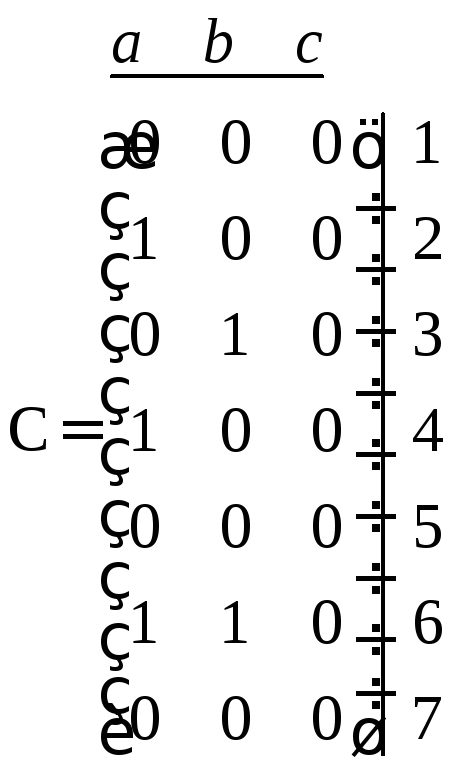Табличный способ задания соответствий

Способы задания функции

Основной признак функциональной зависимости между двумя переменными величинами — это наличие соответствия между значениями этих величин: каждому допустимому значению одной переменной соответствует строго определённое значение другой.

Функция считается заданной, как только установлено соответствие между двумя переменными. Это соответствие может быть установлено различными способами. Рассмотрим подробнее три из них: аналитический, табличный и графический.

Аналитический способ

Аналитический способ — это способ задания функции с помощью формулы.

Например, формула y = x — 2 показывает, как с помощью значения аргумента x вычислить соответствующее ему значение функции y.

Табличный способ

Табличный способ — это способ задания функции с помощью таблицы со значениями.

Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определённая температура (T). Такое соответствие можно записать в виде таблицы:

t (ч)	0	1	2	3	4	5	6	7	8	9	10	11
T (°)	14	14	14,5	14,5	15	15	16	16	16	16,5	16,5	17
t (ч)	12	13	14	15	16	17	18	19	20	21	22	23
T (°)	18	20	22	24	24,5	24,5	24	23	21	20	18	16

Следовательно, T функция от t — T(t) , определённая с помощью множества целых чисел от 0 до 24 и заданная таблицей. Соответствие между величинами двух переменных задаётся в данном случае не формулой, а таблицей.

Графический способ

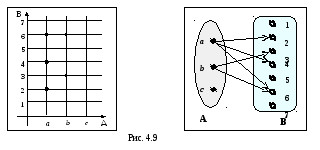
Графический способ — это способ задания функции с помощью графика. В этом случае аргумент является абсциссой точки, а значение функции, соответствующее данному аргументу, ординатой.

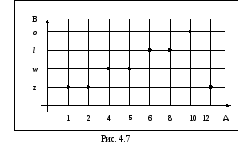
Графики позволяют быстро находить значение функции по значению аргумента и наоборот — значение аргумента по значению функции. Например, рассмотрим уже готовый график функции:

Чтобы узнать, какое значение функции будет соответствовать аргументу x = 1, надо провести из соответствующей точки оси абсцисс (оси x) перпендикуляр на график. Ордината точки пересечения перпендикуляра с графиком (точки M) и будет соответствующим значением функции. Поэтому, так как точка M имеет координаты (1; 2), то запись этих значений в виде функции будет выглядеть так: y(1) = 2.

Источник

4.5. Способы задания бинарных соответствий

Соответствие может быть задано перечислением всех упорядоченных пар, находящихся в соответствии G и соответствующих множеств (см. предыдущий пункт). Очевидно, что такой способ задания приемлем только для относительно небольших по мощности множеств.

Матричный способ. Соответствие G задаётся прямоугольной (квадратной) матрицей С = [  _ij ], где

.

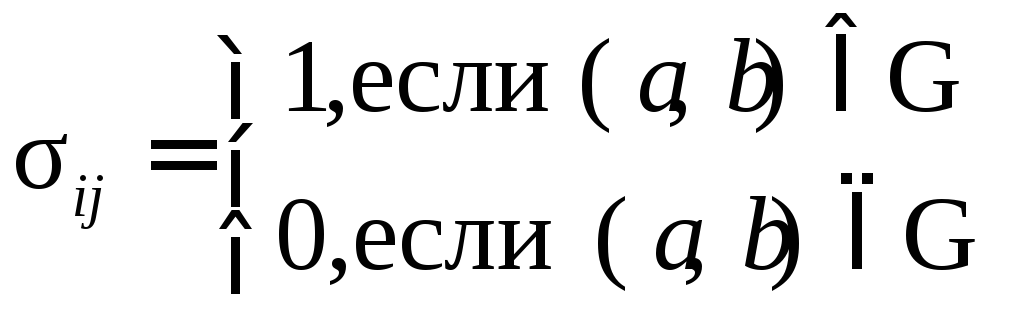
Табличный способ. Для задания этим способом соответствия G проводят вертикали, каждой присваивают значение элемента первого множества А, затем горизонтали, которые получают имена элементов второго множества В. Затем жирными точками обозначают пересечение этих прямых, удовлетворяющих соответствию G. Иногда такая таблица называется графиком соответствия.

Графический способ. Элементы обоих множеств изображаются точками, кружочками или другими геометрическими фигурами. Стрелками же соединяются те элементы множеств, которые принадлежат данному соответствию. Стрелки направлены из области отправления (множество А) к области прибытия (множество В). Такой способ иногда называют стрелочным представлением соответствия.

С помощью сечений. Пусть (a,b)  G. Тогда сечением множества G по элементу а (или левым сечением) называется множество, равное множеству образов этого элемента δ(a,G) = <bbB, (а, b)G>. Сечением G по элементу b (или правым сечением) называется множество, равное множеству прообразов этого элемента δ ─1 (b, G) = <aaA, (а, b)G>. Если под каждым элементом множества А записать соответствующее сечение, то получим новый способ задания соответствия G – с помощью сечений. Множество сечений соответствия G называется фактор-множеством по данному соответствия и обозначается F/G.

Задача 4.5.1. Задать бинарное соответствие на множествах всеми возможными способами.

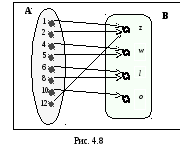
Решение. Для удобства элементы множества А обозначим числами: A = <6, 5, 2, 8, 10, 1, 4, 12>, a элементы множества В буквами: B = <z, w, l, o>. Это позволит нам в дальнейшем отвлечься от конкретного смысла элементов множеств и получить соответствие в формализованном виде.

Задание перечислением: G = <(6,l), (5,w), (2,z), (8,l), (10,o), (1,z), (4,w), (12,z)>. Это позволит нам в дальнейшем отвлечься от конкретного смысла элементов множеств и получить соответствие в формализованном виде.

Задание матричным способом:

Соответствие G состоит из восьми упорядоченных пар. Поэтому матрица С имеет 8 единиц, соответствующих этим парам. Остальные элементы матрицы нули, поскольку соответствующих пар в G нет.

Задание табличным способом:

Полученная таблица напоминает привычный график, например, функции y = f(x), построение которого изучалось в курсе высшей математики. Здесь на оси абсцисс откладываются элементы первого множества (первая проекция соответствия), а на оси ординат – второго множества (вторая проекция).

Задание графическим способом.

Задание с помощью сечений. Сечения лучше всего определять по графику соответствия. Запишем матрицу, где первая строка– это элементы множества А, а вторая строка — соответствующие сечения по каждому элементу множества А:

Фактор-множество по соответствию G записано во второй строке: F/G = <<z>,<w>,<l>,>.

Задача 4.5.2. Бинарное соответствие на множествах А = <a, b, c>; B = <1,2,3,4,5,6,7>задано перечислением: G = <(a,2), (b,3), (a,4), (a,6), (b,6)>. Рассмотреть иные способы задания этого соответствия.

Задание матричным способом:

Задание табличным способом: Задание графическим способом:

Задание с помощью сечений. .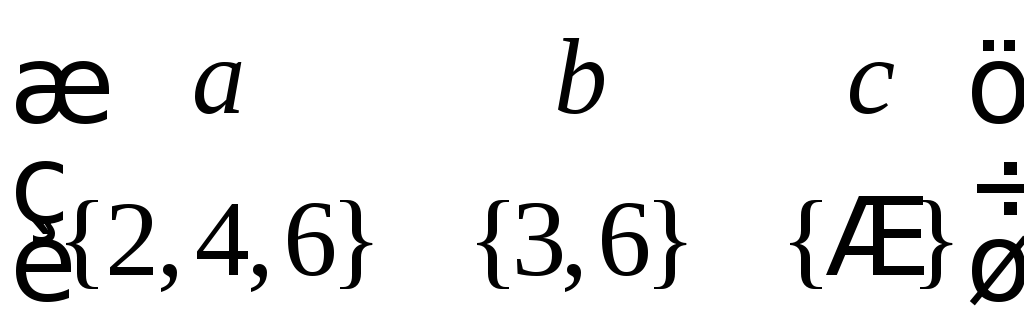

Задачи для самостоятельного решения.

1. Задать бинарное соответствие на множествах всеми возможными способами. А = <Т.Шевченко, А.Пушкин, Л.Украинка, Л.Толстой, У.Шекспир>;

2. На множествах A = <0,1,2,3,4>и B = <5,6,7,8,9>заданы соответствия:

Задать соответствия всеми возможными способами.

Источник

Соответствие

Соответствие. Отображение. функция.

Изучая окружающий нас мир, математика рассматривает не только его объекты, но связи между ними. Эти связи называют по-разному – зависимостями, соответствиями, отображениями, функциями. Примерами таких связей могут быть следующие:

1) С точки зрения правил ГАИ каждому дорожному правонарушению соответствует определенная сумма штрафа. Здесь можно рассмотреть два множества: A – множество видов правонарушений, B – множество штрафов. При этом каждому элементу множества A соответствует один (или несколько) элементов множества B.

2) Для различных моделей огнестрельного оружия используются различные типы патронов. Если A – множество типов патронов и B – множество моделей оружия, то элементу множества A может быть поставлен в соответствие один или несколько элементов множества B, то есть между элементами множества A и элементами множества B может быть установлено соответствие.

3) В школе каждый ученик сидит в классе за строго определенной партой. Если A – множество учеников и B – множество парт, то элементу множества A может быть поставлен в соответствие один элемент множества B, то есть между элементами данных множеств может быть установлено соответствие.

Если элементы двух множеств A и B различной природы сопоставить между собой по какому-либо правилу, т.е. для некоторых элементов aÎA указать один или несколько элементов множества B, то может быть сформировано множество R пар , являющееся подмножеством прямого произведения множеств A и B, т.е.

При этом не обязательно, чтобы в сопоставлении участвовали все элементы множеств A и B.

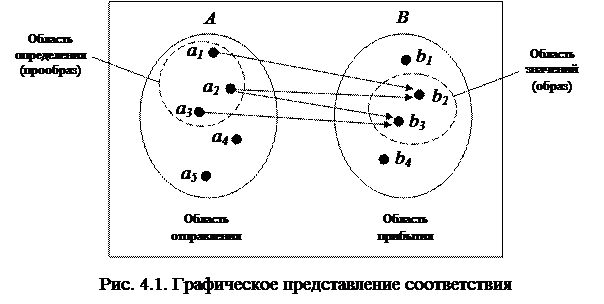
С математической точки зрения соответствием называется тройка множеств: . Множество A называют областью отправления соответствия R, множество B – областью прибытия, множество R – называют законом соответствия или графиком соответствия между множествами A и B.

называется областью определения соответствия R, или прообразом.

называется областью значений соответствия R, или образом.

Термины «образ» и «прообраз» применяются не только ко множествам, но и к отдельным элементам. Так, если элементу a_i соответствует элемент b_j, то a_i является прообразом элемента b_j, а элемент b_j является образом элемента a_i.

В графическом виде соответствие показано на рис. 4.1.

Способы задания соответствий:

1. Графический. При данном способе области отправления и прибытия изображаются в виде овалов или прямоугольников, их элементы изображаются в виде точек внутри соответствующих областей. Соответствия между элементами – стрелками. Пример показан на рис. 4.1.

2. Перечисление пар. Для небольших множеств можно перечислить все пары, образующие данное соответствие. Например, если A – множество мальчиков некоторой студенческой группы, а B – множество девочек этой группы, то соответствие, показывающее, кто из мальчиков влюблен в какую девочку, может быть задано перечислением:

3. Табличный способ. Строится таблица (матрица), в которой строкам соответствуют элементы множества A, а столбцам – элементы множества B. На пересечении строки a_i и столбца b_i ставится единица, если элемент b_i соответствует элементу a_i, и ноль в противном случае. Полученная таким образом таблица называется матрицей инциденций (инциденция – соответствие). Например, чтобы отобразить, кто из мальчиков студенческой группы влюблен в девочек, можно составить следующую матрицу инциденций:

R	Петрова	Андреева	Семенова	Павлова	Игнатова
Иванов
Бережной
Смирнов
Карпов
Гуляев
Корольков

В данной таблице единиц немного, и в подавляющем большинстве клеток записаны нули. Чтобы улучшить читабельность таблицы, нули не показаны, но подразумевается, что они записаны во всех пустых клетках.

4. Словесный способ. В некоторых случаях удается описать соответствие несложной словесной фразой. Фраза должна быть составлена таким образом, чтобы однозначно определить все связи (или их отсутствия) между элементами множеств.

Понятно, что словесный способ задания соответствия возможен не всегда. Если попытаться словесно описать пример соответствия с влюбленными студентами, то все сведется к простому перечислению пар, ибо никакой закономерности между фамилиями влюбленных студентов и студенток нет.

Словесный способ может быть применен, например, в следующем случае. При подготовке выпускного школьного бала был запланирован танец вальс. Чтобы пары танцующих смотрелись гармонично, было решено расположить всех мальчиков и девочек по росту (полагая, что в классе нет двух мальчиков и двух девочек с абсолютно одинаковым ростом), и самый высокий мальчик должен был танцевать с самой высокой девочкой, второй по росту мальчик – со второй по росту девочкой и т.д. Такая расстановка пар есть ни что иное, как задание соответствия между элементами множества мальчиков и множества девочек, причем соответствие задано словесным способом.

Очевидно, что если задание соответствия словесным способом возможно, то мы получаем наиболее краткое задание соответствия, что особенно эффективно для множеств большой мощности.

5. Аналитический способ. По своему принципу подобен словесному способу, но опирается не на слова, а на математические действия. Применение этого способа возможно тогда, когда элементами множеств являются числа.

Например, преподаватель намерен провести контрольную работу в группе из 30 студентов. Однако у преподавателя есть только 8 вариантов заданий, которые нужно каким-то образом распределить между студентами (то есть задать соответствие между множеством студентов и множеством вариантов заданий). Преподаватель нумерует студентов от 1 до 30 (собственно, студенты уже пронумерованы в журнале группы) и нумерует варианты заданий от нуля до семи. Преподаватель рисует на доске все варианты заданий и говорит: «Каждый студент, зная свой номер по журналу N, вычисляет число V = N mod 8, где mod – операция получения остатка от целочисленного деления числа N на 8. Полученное число V и есть номер варианта задания».

В данном примере фраза «V = N mod 8» является аналитическим (вычисляемым) выражением и представляет собой аналитический способ задания соответствия. Если у преподавателя возникнет необходимость провести такую же контрольную среди 1000 студентов, то способ выбора варианта задания не изменится.

1. Соответствие называется полностью определённым (полным слева) (рис. 4.2), если каждому элементу множества A может быть сопоставлен хотя бы один элемент во множестве B; в противном случае соответствие называется частичным.

Источник