Табличный способ задания конечно

Содержание

Способы задания автомата (Лекция)
Табличное задание автомата
Задание автомата диаграммой Мура
Задание конечного автомата системой булевых функций
Способы задания конечных автоматов
Табличный способ задания конечно

Способы задания автомата (Лекция)

1. Табличный способ

2. Графический способ задания автомата

Чтобы задать конечный автомат S, необходимо описать все элементы множества S = , т.е. необходимо описать входной, выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l . При этом среди множества A = 0,a₁,…, a_n > необходимо выделить начальное состояния a0, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический.

При этом способе автомат Мили описывается двумя таблицами: таблицей переходов и таблицей выходов.

Строки этих таблиц соответствуют входным сигналам x ( t ), а столбцы – состояниям. На пересечении столбца a_i и строки x_j в таблице переходов ставится состояние a_s = d [ a_i,x_j ], в которое автомат перейдет из состояния a_i под воздействием сигнала x_j ; а в таблице выходов – соответствующий этому переходу выходной сигнал y_g = l [ a_i,x_j ].

Совмещенная таблица переходов и выходов автомата Мили:

Задание таблиц переходов и выходов полностью описывает работу конечного автомата, поскольку задаются не только сами функции переходов и выходов, но и также все три алфавита: входной, выходной и алфавит состояний.

Для задания автомата Мура требуется одна таблица, поскольку в этом автомате выходной сигнал однозначно определяется состоянием автомата.

Отмеченная таблица переходов автомата Мура :

В этой таблице каждому столбцу приписан, кроме состояния a_i , еще и выходной сигнал y ( t ) = l ( a ( t )), соответствующий этому состоянию. Таблица переходов автомата Мура называется отмеченной потому, что каждое состояние отмечено выходным сигналом.

Приведем примеры табличного задания автоматов Мили и Мура :

По этим таблицам можно найти реакцию автомата на любое входное слово. Например.

Для автомата Мили: Для автомата Мура :

2. Графический способ задания автомата (задание автомата с помощью графа)

Этот способ основан на использовании ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги – переходам между ними. Две вершины графа a_i и a_s соединяются дугой, направленной от a_i к a_s , если в автомате имеется переход из a_i в a_s , т.е. a_s = d ( a_i , x_j ). В автомате Мили дуга отмечается входным сигналом x_j , вызвавшим переход, и выходным сигналом y_g , который возникает при переходе. Внутри кружочка, обозначающего вершину графа, записывается состояние. Например, для автомата Мили, приведенного выше, граф имеет вид а), а для автомата Мура вид б).

Источник

Табличное задание автомата

Из определения автомата следует, что его всегда можно задать таблицей с двумя входами, содержащей m строк и n столбцов, где на пересечении столбца q и строки a стоят значения функций φ(a_i; q_j); ψ(a_i; q_j).

Задание автомата диаграммой Мура

Другой способ задания конечного автомата – графический. При этом способе состояния автомата изображают кружками, в которой вписывают символы состояний q_j (j=1,…,n). Из каждого кружка проводится m стрелок (ориентированных ребер) взаимно-однозначно соответствующих символам входного алфавита X1,…,a_m>. Стрелке, соответствующей букве a_i ϵ X и выходящей из кружка q_j ϵ Q, приписывается пара (a_i, ψ(a_i;q_j)), причем эта стрелка ведет в кружок, соответствующий φ(a_i, q_j).

Полученный рисунок называется графом автомата или, диаграммой Мура. Для не очень сложных автоматов этот способ более нагляден, чем табличный.

Задание конечного автомата системой булевых функций

Третий способ задания конечного автомата А= (X; Q; Y; φ; ψ), заданного таблицей или диаграммой Мура, состоит в определении системы булевых функций.

Изложим алгоритм этого способа задания.

Находим числа k, r, s, удовлетворяющие условиям 2 k -1 k ; 2 r -1 r ; 2 s -1

s , где m=|X|; n=|Q|; p=|Y|.

Очевидно, что k, r, s соответственно равны числу разрядов в двоичном представлении чисел m, n, p. Например, если m=5, n=17, p=3, то k=3, r=5, s=2.

Кодирование состояний входных и выходных символов исходного автомата.

Каждому q_j ϵ Q взаимно-однозначно ставим в соответствие двоичную последовательность длины r – двоичный код α (q) =z₁z₂…z_r. Аналогично каждому a_i ϵ X и каждому b_k ϵ Y ставим взаимно однозначно в соответствие двоичные последовательности β(α)=x₁x₂…x_k; γ(b)=y₁y₂…y_s.

Отметим, что кодирование состояний, входных и выходных символов можно провести многими способами. При этом некоторые последовательности (коды) могут оказаться неиспользованными.

Составляем следующую таблицу:

Код входного символа

Код текущего состояния

Код следующего состояния

Код выходного символа

Эта таблица содержит k+r+r+s столбцов и 2 k + r строк. В первых k+r столбцах выписаны все наборы длины k+r. Каждый такой набор соответствует паре (β, α), где α – возможный код некоторого состояния, β – код входного символа.

Заполнение последних столбцов в таблице (предыдущий шаг).

Для каждой пары (a_i, q_j), где a_i ϵX; q_j ϵQ, находим β(ф) b α(q). По таблице автомата (или диаграмме Мура) определяем φ(a;q)=q ’ и ψ(a;q)=b. Затем находим код α(q ’ )=α₁ ’ α₂ ’ … α_r ’ и код γ(β)=γ₁ γ₂ …γ_s. В строку таблицы, соответствующую набору

Определение системы булевых функций.

После выполнения предыдущего шага может оказаться, что не все строки в таблице заполнены. Это произойдет в том случае, если хотя бы одно из чисел m, n не является степенью 2. Таким образом, функции φ₁, φ₂, …, φ_r, ψ₁, ψ₂, … ψ_s окажутся не полностью определенными – на некоторых наборах их значения не определены. Тогда мы их доопределяем произвольным образом. Как правило, доопределение функций производят так, чтобы получившиеся полностью определенные функции удовлетворяли тем или иным условиям оптимальности, например представлялись минимальными ДНФ.

После выполнения этого шага исходный автомат будет задаваться системой полностью определенных булевых функций

Примеры конечных автоматов

Одним из критериев сложности конечного автомата число его состояний. Чем меньше это число, тем проще дискретное устройство, реализующее данный автомат. Поэтому одной из важных задач теории конечных автоматов является построение автомата с наименьшим числом состояний.

Поскольку в современных компьютерах любая информация представляется в виде двоичных кодов, то для построения автомата можно использовать элементы, имеющие лишь два различных устойчивых состояния, одно из которых соответствует цифре 0, а другое цифре 1.

Приведем несколько примеров конечных автоматов.

Пример 1. Элемент задержки (элемент памяти).

Элементы задержки представляют собой устройство, имеющее один вход и один выход. Причем значение выходного сигнала в момент времени t совпадает со значением сигнала в предыдущий момент. Схематично элемент задержки можно изобразить следующим образом (рис. 2).

Предположим, что входной и, следовательно, выходной алфавит есть Х=<0, 1>; Y=<0, 1>. Тогда Q=<0, 1>. Под состоянием элемента задержки в момент времени t понимается содержание элемента памяти в данный момент. Таким образом q(t)=X(t-1), а Y(t)=q(t)=X(t-1).

Зададим элемент задержки таблицей, где a₁=0, a₂=1, q₁=0, q₂=1,

Источник

Способы задания конечных автоматов

Представление конечного автомата фактически сводится к описанию задающих его автоматных функций. [8]

Существуют три способа задания конечных автоматов:

· Табличный (матрицы переходов и выходов);

· Графический (с помощью графов);

· Аналитический (с помощью формул).

Аналитический способ – автомат задаетсясистемой уравнений. Из такой системы следует, что при конечном числе возможных внутренних состояний количество возможных значений автоматных функций также оказывается конечным. Примером такого задания служат системы уравнений, задающие автоматы Мили и автоматы Мура

Табличный способ.Составляется таблица состояния автоматадля функции перехода – δ и функции выхода. При этом:

· столбцы таблицы соответствуют элементам входного алфавита X,

· строки таблицы соответствуют состояниям (элементы конечного множества Q).

Пересечению i-и строки и j-го столбца соответствует клетка (i, j), которая является аргументом функций 8 и λ автомата в момент, когда он находится в состоянии q_i на его входе – слово x_j, а в самой соответствующей клетке запишем значения функций 8 и λ. Таким образом, вся таблица соответствует множеству Q х X.

При заполнении таблицы переходов каждая клеточка однозначно определяется парой символов: символом следующего состояния и символом выходного сигнала.

На практике автоматные функции задаются двумя конечными таблицами, именуемыми соответственно матрицей перехода и матрицей выводов. При этом строки обозначаются буквами входного алфавита, а столбцы буквами внутреннего алфавита (символами, кодирующими внутреннее состояние автомата).

В матрице переходов на пересечении строки x_k и столбца q_r помещается значение функции перехода δ(q_i, х) и функции выводов λ(q, х). В ряде случаев обе таблицы объединяются в одну таблицу.

Графический способ.

Автомат задается с помощью графа, схемы, графика и др. Задание с помощью ориентированного графа – более удобная и компактная форма описания автомата.

Граф автомата содержит

· Вершины, соответствующие состоянию q_iÎQ,

· Дуги, соединяющие вершины – переходы автомата из одного состояния в другое. На дугах принято указывать пары входных и выходных сигналов – сигналов переходов.

Если автомат переходит из состояния q₁ в состояние q₂ под воздействием нескольких входных сигналов, то на соответствующей дуге графа этот вариант будет представлен через дизъюнкцию. Для представления автомата используют двухполюсные графы с выделенными начальным и конечным состояниями.

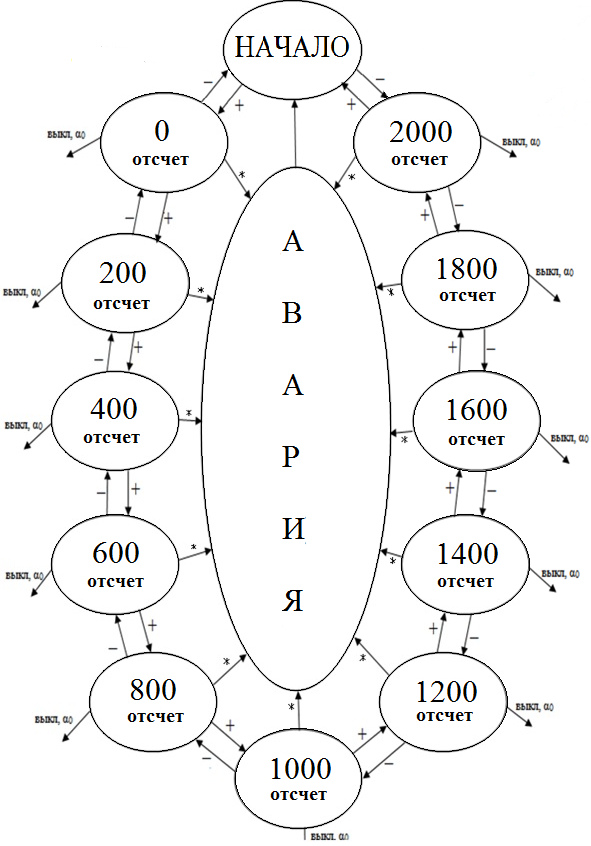
Разработка шкалы «прибора для измерения емкости»

№	индикация	+	—	перегруз.	выкл.	┤
0	исх.сост.	1	0	0	0	нет
1	0	2	0	13	0	да
2	50	3	1	13	0	да
3	100	4	2	13	0	да
4	150	5	3	13	0	да
5	200	6	4	13	0	да
6	250	7	5	13	0	да
7	300	8	6	13	0	да
8	350	9	7	13	0	да
9	400	10	8	13	0	да
10	450	11	9	13	0	да
11	500	13	10	13	0	да
12	ОВ	0	0	0	0	нет
13	авария	0	0	0	0	нет

Рис.2.5. Граф шкалы прибора для измерения емкости

Заключение

Поскольку применение генераторов с колебательными контурами (типа RC) для генерирования колебаний высокой частоты не удовлетворяет, для разрабатываемого генератора была взята схема типа LC (в качестве фазирующей цепочки взята трехточечная схема с автотрансформаторной связью, активный элемент — транзистор).

В теоретической части данной курсовой работы были рассмотрены элементы генераторов LC-типа. Также была рассмотрена классификация генераторов LC-типа, их назначение, а также различные схемы генераторов. А также технические характеристики элементов генераторов.

В практической части была раскрыта тема, касающаяся шифраторов, дешифраторов, их назначения, а также были спроектированы электрические функциональные и электрические принципиальные схемы шифраторов и дешифраторов. Была раскрыта тема карт Карно. Также был разработан сегмент “b” семисегментного индикатора. Был разработан конечный автомат для шкалы прибора для измерения емкости, а также граф для него.

Дата добавления: 2018-02-18 ; просмотров: 2772 ; Мы поможем в написании вашей работы!

Источник

Табличный способ задания конечно

Представление конечного автомата фактически сводится к описанию задающих его автоматных функций.

Существуют три способа задания конечных автоматов:

· Табличный (матрицы переходов и выходов);

· Графический (с помощью графов);

· Аналитический (с помощью формул).

Табличный способ. Составляется таблица состояния автоматадля функции перехода – δ и функции выхода. При этом:

· столбцы таблицы соответствуют элементам входного алфавита X,

· строки таблицы соответствуют состояниям (элементы конечного множества Q).

Пересечению i-и строки и j-го столбца соответствует клетка (i, j), которая является аргументом функций 8 и λ автомата в момент, когда он находится в состоянии q i на его входе – слово x j , а в самой соответствующей клетке запишем значения функций 8 и λ. Таким образом, вся таблица соответствует множеству Q х X.

На практике автоматные функции задаются двумя конечными таблицами, именуемыми соответственно матрицей перехода и матрицей выводов . При этом строки обозначаются буквами входного алфавита, а столбцы буквами внутреннего алфавита (символами, кодирующими внутреннее состояние автомата).

В матрице переходов на пересечении строки x k и столбца q r помещается значение функции перехода δ(q i , х) и функции выводов λ(q, х) . В ряде случаев обе таблицы объединяются в одну таблицу.

Граф автомата содержит

· Вершины, соответствующие состоянию q i ÎQ,

Если автомат переходит из состояния q 1 в состояние q 2 под воздействием нескольких входных сигналов, то на соответствующей дуге графа этот вариант будет представлен через дизъюнкцию. Для представления автомата используют двухполюсные графы с выделенными начальным и конечным состояниями.

Разработка шкалы «прибора для измерения емкости»

№	индикация	+	—	перегруз.	выкл.	┤
0	исх.сост.	1	0	0	0	нет
1	0	2	0	13	0	да
2	50	3	1	13	0	да
3	100	4	2	13	0	да
4	150	5	3	13	0	да
5	200	6	4	13	0	да
6	250	7	5	13	0	да
7	300	8	6	13	0	да
8	350	9	7	13	0	да
9	400	10	8	13	0	да
10	450	11	9	13	0	да
11	500	13	10	13	0	да
12	ОВ	0	0	0	0	нет
13	авария	0	0	0	0	нет

Рис.2.5. Граф шкалы прибора для измерения емкости

1. Табличный способ

2. Графический способ задания автомата

Чтобы задать конечный автомат S, необходимо описать все элементы множества S = , т.е. необходимо описать входной, выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l . При этом среди множества A = необходимо выделить начальное состояния a0, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический.

При этом способе автомат Мили описывается двумя таблицами: таблицей переходов и таблицей выходов.

Строки этих таблиц соответствуют входным сигналам x (t ), а столбцы – состояниям. На пересечении столбца a i и строки x j в таблице переходов ставится состояние a s = d [ a i ,x j ], в которое автомат перейдет из состояния a i под воздействием сигнала x j ; а в таблице выходов – соответствующий этому переходу выходной сигнал y g = l [ a i ,x j ].

Совмещенная таблица переходов и выходов автомата Мили:

d (a 0 ,x 1)/ l (a 0 ,x 1)

d (a n ,x 1)/ l (a n ,x 1)

d (a 0 ,x m)/ l (a 0 ,x m)

d ( a n ,x m )/ l ( a n ,x m )

Отмеченная таблица переходов автомата Мура :

В этой таблице каждому столбцу приписан, кроме состояния a i , еще и выходной сигнал y (t ) = l (a (t )), соответствующий этому состоянию. Таблица переходов автомата Мура называется отмеченной потому, что каждое состояние отмечено выходным сигналом.

Приведем примеры табличного задания автоматов Мили и Мура :

По этим таблицам можно найти реакцию автомата на любое входное слово. Например.

Для автомата Мили:Для автомата Мура :

x 1 x 2 x 2 x 2 x 1 …x 1 x 2 x 2 x 2 x 1 …

a 0 a 1 a 0 a 0 a 0 a 1 a 0 a 2 a 4 a 1 a 4

y 1 y 1 y 2 y 2 y 1 y 2 y 1 y 2 y 1 y 2

2. Графический способ задания автомата (задание автомата с помощью графа)

Этот способ основан на использовании ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги – переходам между ними. Две вершины графа a i и a s соединяются дугой, направленной от a i к a s , если в автомате имеется переход из a i в a s , т.е. a s = d (a i , x j ). В автомате Мили дуга отмечается входным сигналом x j , вызвавшим переход, и выходным сигналом y g , который возникает при переходе. Внутри кружочка, обозначающего вершину графа, записывается состояние. Например, для автомата Мили, приведенного выше, граф имеет вид а), а для автомата Мура вид б).

Элементы теории автоматов

1. Понятие автомата, принцип работы автомата

2. Способы задания конечных автоматов

3. Общие задачи теории автоматов

Человек всегда стремился к тому, что бы облегчить свой труд, заставляя работать на себя некоторые механические устройства без собственного вмешательства. Вначале это были сказки, затем они стали превращаться в обыденные вещи. Автомобиль, телевизор, стиральные машины, целые производства работают без участия человека. Причем, вмешательство человека в большинстве случаев не требуется, а в ряде случаев, такое вмешательство может привести к негативным явлениям. Понятие «автомат», как некоторое устройство, выполняющее определенный вид действий давно трактуется людьми именно так.

Понятие автомата, принцип работы автомата

Понятие автомат рассматривается в двух аспектах:

1. Автомат – устройство , выполняющее некоторые функции без непосредственно участия человека. Автомат это реальное устройство, понятное, почему и как оно работает, хотя бы для тех людей, которые его сконструировали и изготовили. Автомобиль, трактор, самолет, светофор, телевизор, телефон – все это автоматы. В этом аспекте ЭВМ следует понимать как автомат, который работает по программе, составленной человеком.

2. Автомат – математическое понятие , обозначающее математическую модель реальных технических устройств. Автомат это абстрактное устройство, непонятно почему и как оно работает и, вообще, почему оно может работать. В этом аспекте автомат есть «черный ящик», который теоретически способен проводить некоторые действия. С точки зрения математики, абсолютно неважно что, как и почему производит те или иные действия.

Любой автомат должен иметь некоторое количество входов, некоторое количество выходов и некоторое количество внутренних состояний.

Алгебраическая теория автоматов является разделом теоретической кибернетики, который изучает дискретные автоматы с абстрактной алгебраической точки зрения.

Общая теория автоматов содержит различные подразделы. В зависимости от предмета изучения она делится на абстрактную теорию автоматов и структурную теорию автоматов.

Абстрактная теория автоматов изучает переходы, совершаемые автоматом, на который воздействуют входные сигналы, а также выходные сигналы как результат этих переходов.

Предметом изучения структурной теории автоматов является структура автомата, а также структура входных и выходных сигналов, например, способы кодирования входных и выходных сигналов и др.

Определение конечных автоматов

Автомат — абстрактная модель устройства, функционирующего в дискретном времени, которая перерабатывает конечную последовательность входных сигналов и превращает их в конечную последовательность выходных сигналов (реакций).

В процессе работы конечного автомата происходит последовательная смена конечного число его внутренних состояний, причем состояние автомата в определенный момент времени однозначно определяется входным и выходным сигналами. Такие автоматы представляют собой основу всей современной вычислительной техники и всевозможных дискретных систем автоматического контроля и управления.

Понятие автомата настолько абстрактное, что трудно сказать, когда человек вообще обходился без каких либо автоматов. Под определение автомата подходят любые устройства, в том числе те, которыми первобытные люди охотились или метали камни, защищая свое жилище от неприятеля.

Алгоритм – понятное и точное формальное предписание исполнителю, однозначно определяющее содержание и последовательность операций, переводящих заданную совокупность исходных данных в искомый результат

Считается, что первым программным устройством, созданным человеком, были часы. Часовые механизмы с помощью пружины, приводящей в действие шестеренки и кулачковые механизмы, зубчатые колеса и рычаги, осуществляют ряд определенных действий. Примером такого часового механизма могут быть знаменитые часы на Центральном театре кукол в Москве, где он приводит в действие двенадцать сказочных героев, расположенных на циферблате.

Укажем несколько любопытных исторических фактов, связанных с автоматами, как механическими устройствами.

1. Немецкий философ и алхимик Альберт Великий с 1216 по 1246 г., создавал «железного» слугу — автомат, который выполнял в доме обязанности привратника.

2. Астроном Иоганн Мюллер (Региамонтан) (1436-1476) создал механического орла, который приветствовал наклоном головы и движением крыльев въезд в Нюрнберг императора священной Римской империи Максимилиана II.

3. Механик Жак де Вакансон (1709-1782) – автор первого в мире автоматического ткацкого станка. Он создал образ механической утки, точной копии своего живого двойника — плавала, чистила перья, глотала с ладони зерна. Его механический флейтист, исполнявший одиннадцать музыкальных пьес, поражал людей, живших в те далекие годы.

4. Русский изобретатель 19 в. А. М. Гамулецкий создал целый механический кабинет, в котором было множество сконструированных им автоматов. Здесь в том числе была и говорящая голова чародея и амур, играющий на арфе, которые поражали воображение современников.

5. Первый примитивный арифмометр сконструировал в 1641 г. Блез Паскаль. Толчком для открытия были мучения его отца – налогового, инспектора, который днями и ночами работал с большими вычислениями. Изобретя арифмометр, восемнадцати летний сын избавил отца от сложных вычислений, а миру подарил первый калькулятор, производящий сложение и вычитание чисел.

6. Первый шахматный автомат был построен в 1890 г. испанским инженером Торресом Кеведо. Такой автомат мог разыграть лишь ладейный эндшпиль (король и ладья против короля).

7. Первую вычислительную машину с автоматическим управлением создал Чарльз Баббедж в 1822 г. Он спроектировал арифмометр , который имел запоминающие и арифметические устройства. Эти устройства стали прототипами аналогичных устройств современным ЭВМ.

Автомат можно трактовать как устройство, выполняющие процессы приема, преобразования и передачи энергии, материалов или информации в соответствии с заложенной в них программой, но без непосредственного участия человека.

Любой автомат имеет собственные базовые множества, которые включают в себя:алфавит входа, алфавит выхода, множество состояний автомата.

Характерной особенностью конечного автомата является наличие памяти, которая определяет состояние автомата в зависимости от времени. Внешним проявлением различных состояний автомата является его реакция на однотипные воздействия (сигналы).

В работе конечных цифровых автоматов важным понятием является время.

Автоматы можно классифицировать по различным признакам.

1. По виду деятельности — автоматы делятся на: информационные, управляющие и вычислительные.

К информационным автоматам относятся разнообразные справочные таблицы, информационные табло на стадионах, устройства аварийной сигнализации.

К управляющим автоматам принято относить устройства для управления некоторым процессом, в том числе конкретно: лифтом, конвейером, станком, шлагбаумом.

К вычислительным автоматам относятся микрокалькуляторы, процессоры в ЭВМ и иные устройства, выполняющие вычисления.

Однако, строго говоря, многие, автоматы представляют собой настолько сложные системы, что они являются одновременно и вычислительными, и управляющими, и информационными автоматами.

2. Конечные автоматы – с точки зренияинформатики это такие автоматы, которые представляют собой дискретные преобразователи информации. К ним относятся преобразователи, в которых содержится конечное множество входных и конечное выходных сигналов, а также конечное множество внутренних состояний

3. Цифровые автоматы — автоматы, которые преобразует цифровую информацию. В таком автомате входные сигналы задаются в виде конечного множества мгновенных символов: их длительность настолько мала, что ею можно пренебречь. За фиксированное время происходит преобразование входных символов, а на выходе происходит скачкообразный переход из одного состояния в другое состояние.

4. Абстрактные автоматы — отображающие множество слов входного алфавита Х во множество слов выходного алфавита Y.

Абстрактный автомат есть:

Алгоритм действия некоторого преобразования кодовых последовательностей,

Закон преобразования входного алфавита в выходной.

5. Синхронные и асинхронные автоматы . В зависимости от того, одновременно или последовательно принимаются входной сигнал и сигнал смены состояний, автоматы делятся насинхронные и асинхронные автоматы.

В синхронных автоматах продолжительность входных сигналов и время переходов согласовано между собой. Они используются в вычислительных комплексах, АСУ и т.д.

В асинхронных автоматах продолжительность входных сигналов и время переходов не согласовано между собой. Они зависят от внешних источников — различных событий, а интервал дискретности является переменным (например, в кодовых замках). В асинхронных автоматах очередное изменение значений входных сигналов может произойти только при условии, что закончился переходный процесс, вызванный предыдущим изменением этих сигналов.

6. Автоматы делятся на конечные и бесконечные автоматы. Если в основании классификации лежит объем памяти, то различие заключается в том, имеет ли автомат конечное или бесконечное число внутренних состояний.

Под бесконечным автоматом обычно понимают определенную математическую идеализацию представлений об автомате, имеющую бесконечное число состояний. Память такого автомата потенциально может неограниченно возрастать. Например, известные абстрактные автоматы Поста и Тьюринга являются бесконечными автоматами, но сама ЭВМ или ее отдельные части — конечными автоматами.

7. Автоматы делятся на детерминированные и вероятностные автоматы . Если в основании классификации лежит механизм случайного выбора, то различают детерминированные и вероятностные (стохастические) автоматы.

В детерминированных автоматах поведение и структура в каждый момент времени однозначно определены текущей входной информацией и состоянием самого автомата в предшествующий момент времени.

В вероятностных автоматах эта зависимость связана еще и с некоторым случайным выбором.

Вероятностный автомат — это дискретный преобразователь информации, функционирование которого в каждый момент времени зависит только от состояний памяти и описывается статистическими законами.

8. Универсальный автомат. В теории автоматов доказано, что для выполнения различных преобразований информации достаточно построить универсальный автомат с помощью программы и соответствующего кодирования, способный решать любые задачи.

Математическая модель цифрового автомата с одним входом задается пятью объектами:

X- конечное множество входных символов, входной алфавит:

Y- конечное множество выходных символов, выходной алфавит:

конечное множество состояний автомата:

δ(q, х ) — функция перехода автомата из одного состояния в другое: (Q х X) ®Q;

функция выхода автомата: (Q x Х) ® Y.

Таким образом, конечный автомат С= (X, Q, У, δ, λ.) определяется рекуррентными соотношениями

q(0) = q 0 , q(t + I) = δ (g(t), х(t)), y(t) = λ (g(t), х(t)),

t- дискретизированный момент времен или это есть образ монотонной функции t :. Т ® N, причем Т — обычное непрерывное время, N — множество натуральных чисел.

Все время работы Т разбивается на конечное число интервалов, на границе которых происходит изменение состояния автомата. При этом t(Г 0) – показывает число изменений, произошедших до момента времени Г 0 .

Примером дискретизации служит обычный кинематограф: время разбито на интервалы длительностью 1/24с. Человеческий глаз воспринимает следование дискретных кадров как непрерывное движение.

9. Синхронные автоматы делятся на автоматы Мили и автоматы Мура . В зависимости от способа организации функции выхода синхронные автоматы делятся на автоматы Мили (автоматы I рода) и автоматы Мура(автоматы II рода).

В автоматах Мили — выходной сигнал y (t) x (t) и состоянием q (t- 1) автомата в предшествующий момент времени (t- 1). Математической моделью таких автоматов служит система уравнений:

q(t) = δ (q(t-1), х(t)) и y(t) = λ (q(t-1), х(t)),

В автоматах Мура выходной сигнал y (t) однозначно определяется входным сигналом x (t) и состоянием q (t) в данный момент времени t. Математической моделью таких автоматов является система:

q(t) = δ (q(t-1), х(t)) и y(t) = λ (q(t)),

В таких автоматах функция выхода зависит только от состояний автомата в данный момент времени и не зависит от входного сигнала. Таким образом, входная строка такого автомата однократно считывается слева направо, осуществляя поочередный просмотр символов. В определенный момент времени конечный автомат находится в некотором внутреннем состоянии, которое изменяется после считывания очередного символа. Новое состояние можно охарактеризовать считанным символом и текущим состоянием.

10. Комбинационные автоматы – есть автоматы, в которых выходной символ не зависит от его состояния и определяется лишь текущими входными символами, т.е. в этом автомате все состояния эквивалентны. В таком автомате вырождена функция перехода, она принципиально не важна и в процессе функционирования неизменна. Поэтому минимальный комбинационный автомат имеет лишь одно состояние.

11 Логические автоматы – есть автоматы у которых входной алфавит состоит из 2 т двоичных наборов длины т, а выходной — из 2 n двоичных наборов длины п. Для логических комбинационных автоматов функция выхода имеет вид системы п логических функций от т переменных.

Для описания конечных цифровых автоматов можно использовать стандартные (автоматные) языки и начальные языки.

Стандартные или автоматные языки описания.

Они описывают функции переходов и выходов в явном виде, а именно в виде:

Таблиц переходов и выходов;

Из определения автомата следует, что его всегда можно задать таблицей с двумя входами, содержащей m строк и n столбцов, где на пересечении столбца q(состояния автомата) и строки а (входные сигналы) стоят значения функций φ(l) (a i ,q j) (функция переходов); \|/ (m )(a i ,q j)(функция выходов).

2) графа, представляющего наглядно функции l и m ..

Другой способ задания конечного автомата — графический. При этом способе состояния автомата изображают кружками, в которые вписывают символы состояний q j (j= 1. п). Из каждого кружка проводится m стрелок

(ориентированных рёбер) взаимно-однозначно соответствующих символам входного алфавита X(V). Стрелке, соответствующейбукве а i X и выходящей из кружка q j Q(S), приписывается пара (а i , \|/ (a i ,q j) , причем эта стрелка ведет в кружок, соответствующий φ (a i ,q j)

Абстрактный автомат Мура это частный случай автомата Мили (4), когда выходной символ зависти только от состояния автомата, а именно функция выходов автомата Мура:

Для каждого автомата Мили можно построить эквивалентный автомат Мура, реализующий точно такой же алфавитный оператор. Пусть A = автомат Мили. В качестве состояний эквивалентного автомата Мура возьмем пары . Тогда функция выходов эквивалентного автомата Мура

а функция переходов

Задание конечного автомата системой булевых функций

Третий способ задания конечного автомата А = (X;Q;Y; φ ;\|/), заданного таблицей или диаграммой Мура, состоит в определении системы булевых функций.

Источник