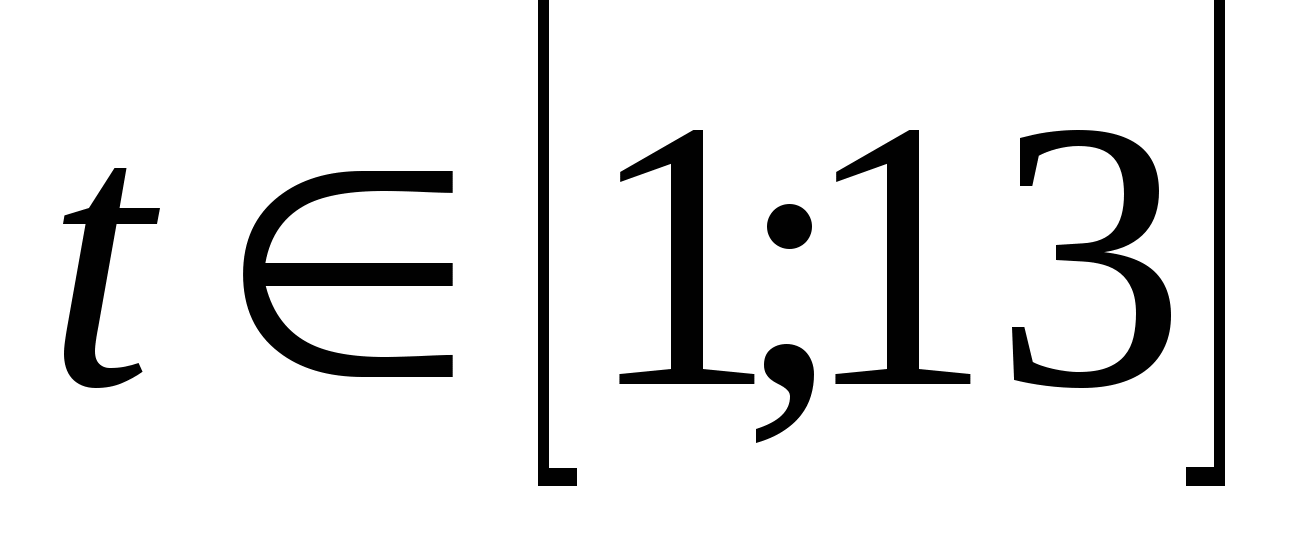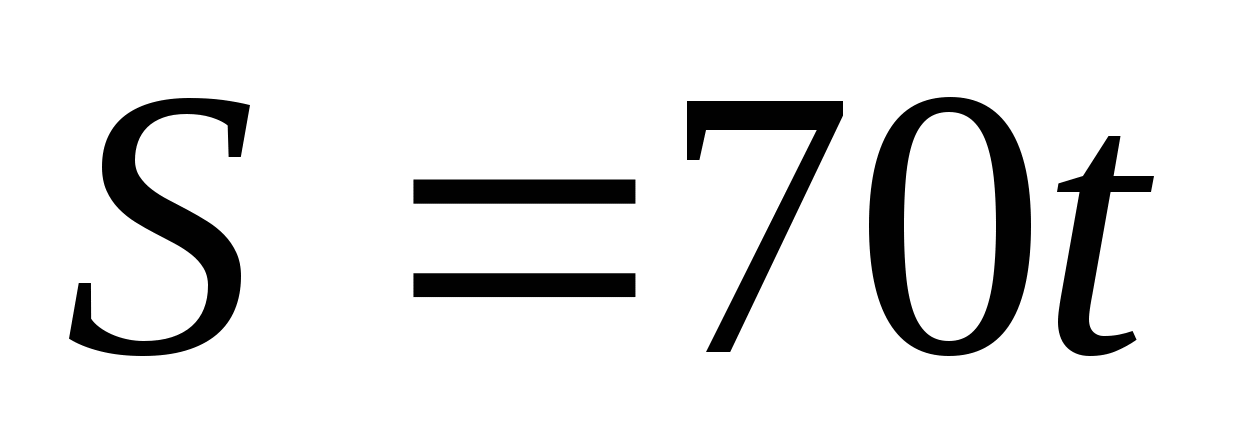Табличный способ задания функции заполните таблицу

Способы задания функций. График функции

Содержание

Определить правило, по которому зависимая величина будет меняться, значит задать функцию. Вариантов задания функции несколько:

1. Словесно, например: «игрек равен двум х». Запись будет выглядеть так: $у = 2\times x$
2. Аналитический способ, то есть сразу с помощью записи формулы, например: $f(x) = x-3$
3. Графический способ
4. Табличный способ

Графический способ

Графический способ подразумевает чертеж на прямоугольной координатной плоскости, например:

Линия, изображенная на рисунке, называется графиком функции.

Линия может быть разной: прямой или кривой.

Функция (и ее график) может быть:

• возрастающей (линия идет вверх, как на рисунке выше), если вторая зависимая величина увеличивается вместе с первой;
• убывающей (линия идет вниз), если вторая величина уменьшается при увеличении первой, например:

Функция (и ее график) может быть убывающей или возрастающей как на всей области определения, так и на определенном промежутке:

Графический способ не дает возможности предельно точного определения численных значений $x$ и $у$, но он наглядно показывает поведение функции (убывает или возрастает, максимум, минимум, непрерывность и т. д.) и является важным способом ее исследования.

Табличный способ

Часто используется табличный (то есть в виде таблицы) способ задания функции. В таблице для каждого значения аргумента $x$ указывается соответствующее ему конкретное значение функции $y$, например:

$x$	$1$	$2$	$3$	$5$
$y$	$10$	$20$	$30$	$50$

Каждое значение аргумента и функции нумеруется. В данном случае в таблице значению $x_1$ , равному $1$ , соответствует единственное значение $у_1$ , равное $10$ . Значению $x_2$ , равному $2$ , соответствует $у_2$ , равное $20$ и т. д.

Не трудно догадаться, что в таблице выше отражена зависимость

Ее можно продолжить для любых значений $x$, так при

$y_<100>$ будет равен $1000$.

Табличный способ позволяет быстро найти конкретные значения $x$ и $у$.

Заполним таблицу для функции

Попробуем заполнить таблицу функции $у=3x+2$, для значений $x$, равных $1$, $3$, $4$, $8$.

Подставим в формулу $у=3x+2$ значения $x_1$, $x_2$, $x_3$, $x_4$.

Источник

Табличный способ задания функции

Урок изучения и закрепления табличного способа задания функции. Повторение и закрепление понятия «Функция».

Просмотр содержимого документа
«Табличный способ задания функции»

Тема: Табличный способ задания функции

Образовательные: Актуализировать знания учащихся о понятии функции, области определения, области значения. Продолжить формирование о понятие табличного способа задания функции, шаге таблицы. Научить определять по таблице значения аргумента по заданным значениям функции и наоборот, определять по таблице формулу функции, заполнять значения аргумента и значения функции. Развивать умение использовать отрезок области определения и шаг изменения аргумента для заполнения таблицы по формуле функции, находить область определения и записывать ее при помощи числового промежутка.

Развивающие: Способствовать логическому мышлению, умению обосновывать, анализировать. Способствовать развитию устных навыков счета, правильной математической речи.

Воспитательные: Способствовать развитию коммуникативных навыков у обучающихся, трудолюбию, умению добиваться своей цели.

1. Организационный этап -1мин

Улыбнитесь мне, друг другу и нашим гостям. Садитесь. Сегодняшний урок я хотела бы чтобы мы провели под девизом: «Верь в себя и говори себе, что ты лучший». Будьте уверены в себе и не бойтесь ошибаться. Ведь не ошибается только тот, кто ничего не делает. А нас ждет впереди интересная работа.

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. У нас всего 40 мин, но мне бы очень хотелось, чтобы они не тянулись, а пролетели. Не оказались прожитыми впустую, а были затрачены с пользой.

На столе у вас у каждого карта самооценивания, где вы будете оценивать свою работу за выполненные задания. Подпишите их.

3. Работа устно-5 мин

Работа устно: работа по карточкам, 6 карточек цепочка оценивание.

Получаем 12.04.1961 чем знаменательна эта дата?

4. Актуализация знаний, проверка готовности учащихся к изучению нового материала. 5 мин

Прежде, чем приступить к уроку, вспомним, о чем мы говорили на прошлом уроке. О функции. Что называется функцией? Где применяются функции?

Учащийся 6 «б» класса сказал, что графики применяются в работе детектора лжи. И мне понравилось эта идея. Предлагаю провести разминку следующим образом: представьте себе, что вы – детектор лжи, если прозвучавшее утверждение – истина, то чертится горизонтальный отрезок, если ложь, то происходит «всплеск», чертится ломанная.

1. Областью определения функции называется множество значений аргумента. (да)

2. Горизонтальная координатная прямая называется осью ординат. (нет)

3. Независимую переменную называют функцией (нет )

4. Зависимую переменную называют аргументом. (нет)

5.Областью значений функции называется множество всех значений функции. (да)

1.Функцией называется зависимость одной переменной от другой, где каждому значению одной переменной, соответствует одно значение другой переменной.(да)

2.Вертикальная координатная прямая называется осью абцисс.(нет)

3. Зависимую переменную называют аргументом.(нет)

4. Независимую переменную называют функцией.(нет)

5. Областью определения функции называется множество значений аргумента.(да)

Взаимопроверка (оценивание).

5. Работа у доски: поставить соответствие, 3 мин.

Найти область определения своей функции, выбрать на листах соответствующий ответ и прикрепить под функцией, перевернув на обратную сторону.

ИТАК ТЕМА НАШЕГО УРОКА: ТАБЛИЧНЫЙ СПОСОБ ЗАДАНИЯ ФУНКЦИИ

Запись в тетради числа и темы.

6.Формирование навыков и умений

Работа по таблице-3мин

1)

2)

3) шаг таблицы равен 2

4) Через какое время автомобиль проедет 490 км, 210 км, 560 км

5) Какое расстояние проедет автомобиль через 5 ч, 11 ч, 13 ч?

6) Какова скорость автомобиля? ()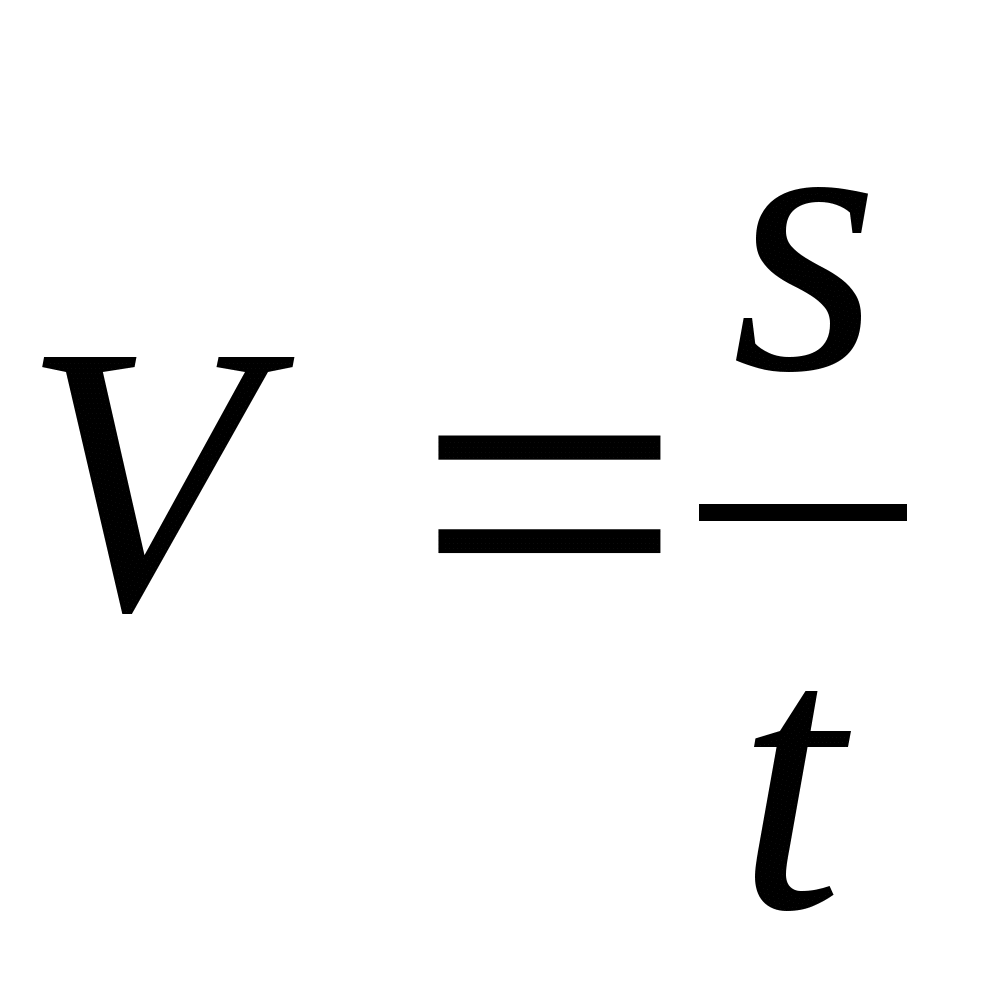

7) формула функции

8. ЗАКРЕПЛЕНИЕ: карточка №2

Работа самостоятельно, 2 человека работают у доски самостоятельно. 3мин

Указать область определения функции

Указать шаг таблицы

Указать область значений функции

С какой скоростью двигался автомобиль?

За какое время автомобиль преодолел 360 км?

Сколько километров проехал автомобиль через 10 ч?

Указать область определения функции

Указать шаг таблицы

Указать область значений функции

С какой скоростью двигался автомобиль?

За какое время автомобиль преодолел 270 км?

Сколько километров проехал автомобиль через 5 ч?

9. Работа в паре. 5мин. № 1294 учебника стр. 134.

Для заданных функций составьте таблицу:

, где , с шагом, равным 2;

где , с шагом, равным 4.

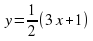
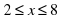
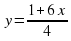
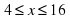
10. Работа в группе. 7мин

Работа по учебнику: № 1286. Работа по таблице. Ответить на вопросы.

№ 1287. Заполнить таблицу, перечертить в тетрадь.

№ 1290. Заполните таблицу, запишите функцию формулой.

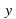
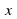
№ 1296. Заполните таблицу, запишите формулой зависимость значений от значений . Выберите правильный ответ.
11.Подведение итогов урока. Выставление оценок за урок.

12.Домашнее задание: п. 8.2, № 1295, 1301.

Источник

Табличный способ задания функции

Урок изучения и закрепления табличного способа задания функции. Повторение и закрепление понятия «Функция».

Просмотр содержимого документа
«Табличный способ задания функции»

Тема: Табличный способ задания функции

Образовательные: Актуализировать знания учащихся о понятии функции, области определения, области значения. Продолжить формирование о понятие табличного способа задания функции, шаге таблицы. Научить определять по таблице значения аргумента по заданным значениям функции и наоборот, определять по таблице формулу функции, заполнять значения аргумента и значения функции. Развивать умение использовать отрезок области определения и шаг изменения аргумента для заполнения таблицы по формуле функции, находить область определения и записывать ее при помощи числового промежутка.

Развивающие: Способствовать логическому мышлению, умению обосновывать, анализировать. Способствовать развитию устных навыков счета, правильной математической речи.

Воспитательные: Способствовать развитию коммуникативных навыков у обучающихся, трудолюбию, умению добиваться своей цели.

1. Организационный этап -1мин

Улыбнитесь мне, друг другу и нашим гостям. Садитесь. Сегодняшний урок я хотела бы чтобы мы провели под девизом: «Верь в себя и говори себе, что ты лучший». Будьте уверены в себе и не бойтесь ошибаться. Ведь не ошибается только тот, кто ничего не делает. А нас ждет впереди интересная работа.

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. У нас всего 40 мин, но мне бы очень хотелось, чтобы они не тянулись, а пролетели. Не оказались прожитыми впустую, а были затрачены с пользой.

На столе у вас у каждого карта самооценивания, где вы будете оценивать свою работу за выполненные задания. Подпишите их.

3. Работа устно-5 мин

Работа устно: работа по карточкам, 6 карточек цепочка оценивание.

Получаем 12.04.1961 чем знаменательна эта дата?

4. Актуализация знаний, проверка готовности учащихся к изучению нового материала. 5 мин

Прежде, чем приступить к уроку, вспомним, о чем мы говорили на прошлом уроке. О функции. Что называется функцией? Где применяются функции?

Учащийся 6 «б» класса сказал, что графики применяются в работе детектора лжи. И мне понравилось эта идея. Предлагаю провести разминку следующим образом: представьте себе, что вы – детектор лжи, если прозвучавшее утверждение – истина, то чертится горизонтальный отрезок, если ложь, то происходит «всплеск», чертится ломанная.

1. Областью определения функции называется множество значений аргумента. (да)

2. Горизонтальная координатная прямая называется осью ординат. (нет)

3. Независимую переменную называют функцией (нет )

4. Зависимую переменную называют аргументом. (нет)

5.Областью значений функции называется множество всех значений функции. (да)

1.Функцией называется зависимость одной переменной от другой, где каждому значению одной переменной, соответствует одно значение другой переменной.(да)

2.Вертикальная координатная прямая называется осью абцисс.(нет)

3. Зависимую переменную называют аргументом.(нет)

4. Независимую переменную называют функцией.(нет)

5. Областью определения функции называется множество значений аргумента.(да)

Взаимопроверка (оценивание).

5. Работа у доски: поставить соответствие, 3 мин.

Найти область определения своей функции, выбрать на листах соответствующий ответ и прикрепить под функцией, перевернув на обратную сторону.

ИТАК ТЕМА НАШЕГО УРОКА: ТАБЛИЧНЫЙ СПОСОБ ЗАДАНИЯ ФУНКЦИИ

Запись в тетради числа и темы.

6.Формирование навыков и умений

Работа по таблице-3мин

1)

2)

3) шаг таблицы равен 2

4) Через какое время автомобиль проедет 490 км, 210 км, 560 км

5) Какое расстояние проедет автомобиль через 5 ч, 11 ч, 13 ч?

6) Какова скорость автомобиля? ()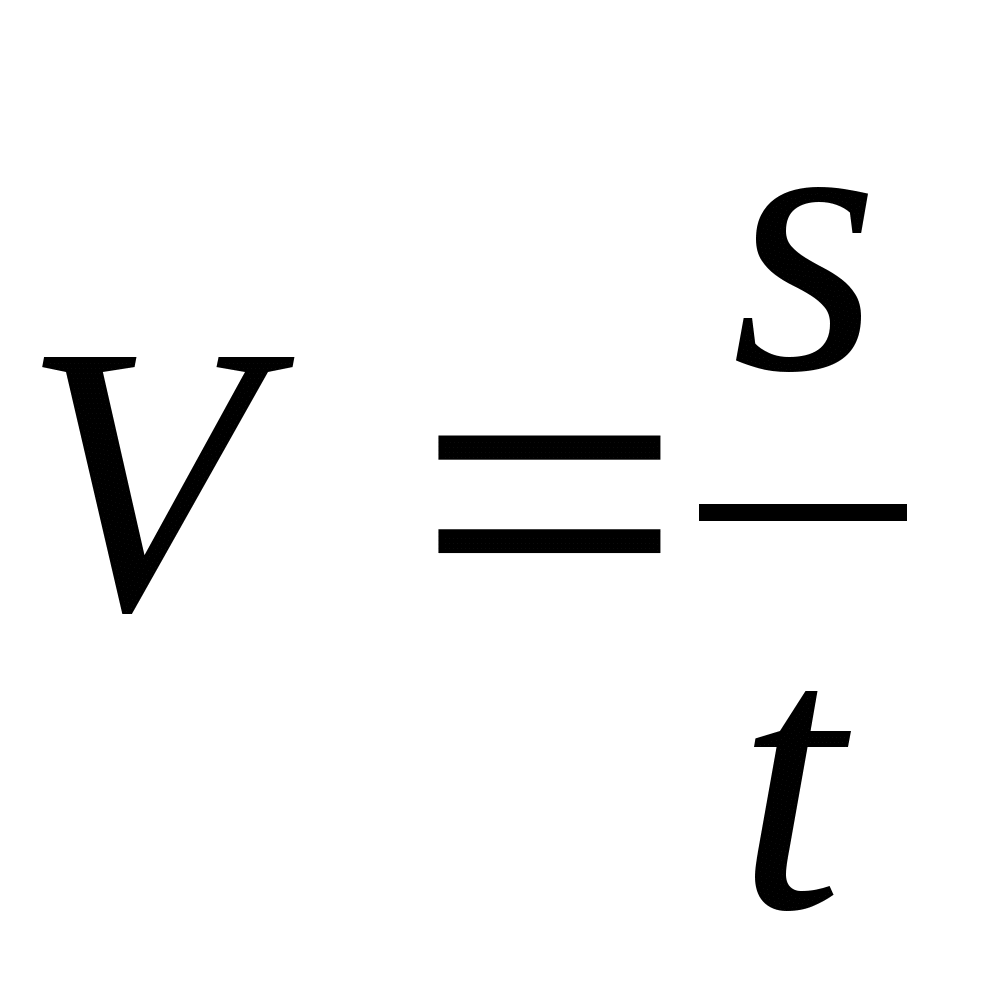

7) формула функции

8. ЗАКРЕПЛЕНИЕ: карточка №2

Работа самостоятельно, 2 человека работают у доски самостоятельно. 3мин

Указать область определения функции

Указать шаг таблицы

Указать область значений функции

С какой скоростью двигался автомобиль?

За какое время автомобиль преодолел 360 км?

Сколько километров проехал автомобиль через 10 ч?

Указать область определения функции

Указать шаг таблицы

Указать область значений функции

С какой скоростью двигался автомобиль?

За какое время автомобиль преодолел 270 км?

Сколько километров проехал автомобиль через 5 ч?

9. Работа в паре. 5мин. № 1294 учебника стр. 134.

Для заданных функций составьте таблицу:

, где , с шагом, равным 2;

где , с шагом, равным 4.

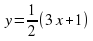
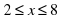
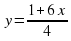
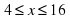
10. Работа в группе. 7мин

Работа по учебнику: № 1286. Работа по таблице. Ответить на вопросы.

№ 1287. Заполнить таблицу, перечертить в тетрадь.

№ 1290. Заполните таблицу, запишите функцию формулой.

№ 1296. Заполните таблицу, запишите формулой зависимость значений 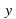от значений . Выберите правильный ответ.
11.Подведение итогов урока. Выставление оценок за урок.

12.Домашнее задание: п. 8.2, № 1295, 1301.

Источник