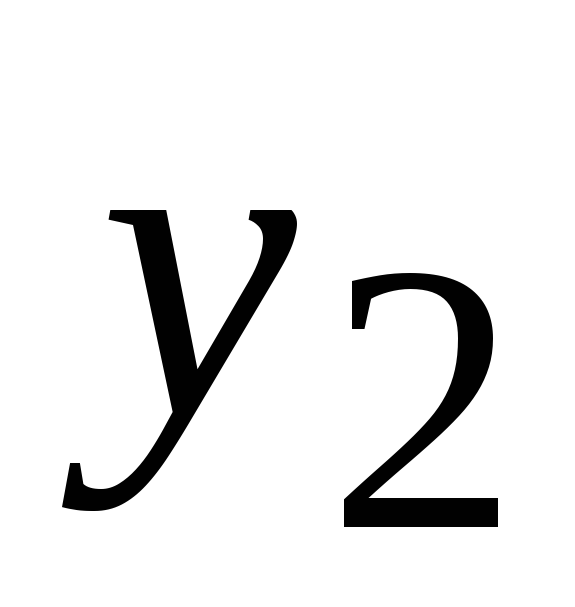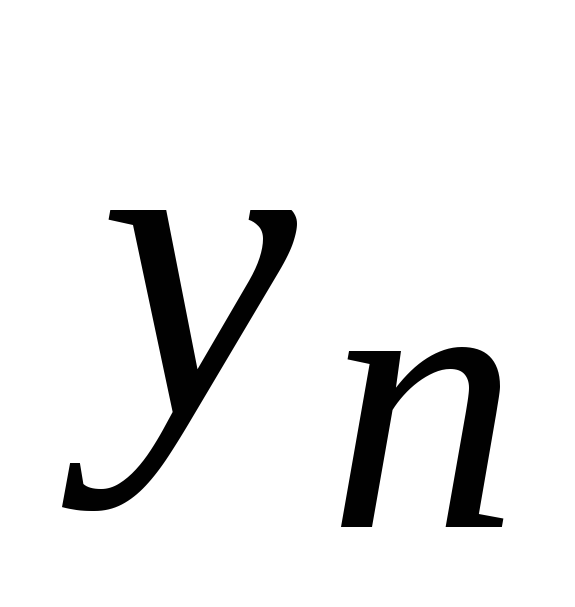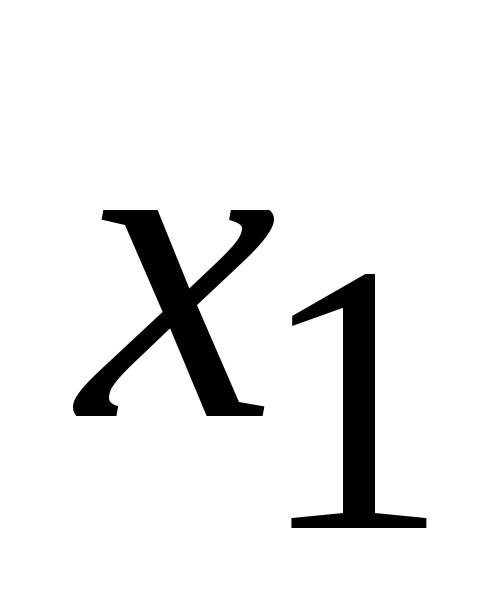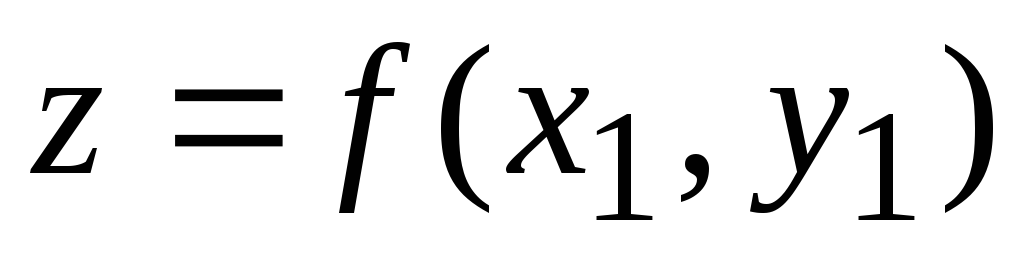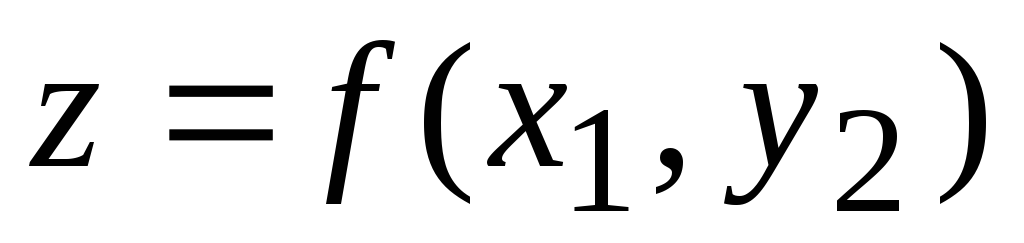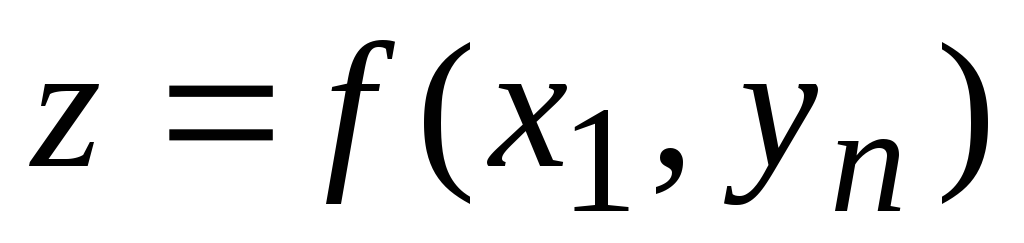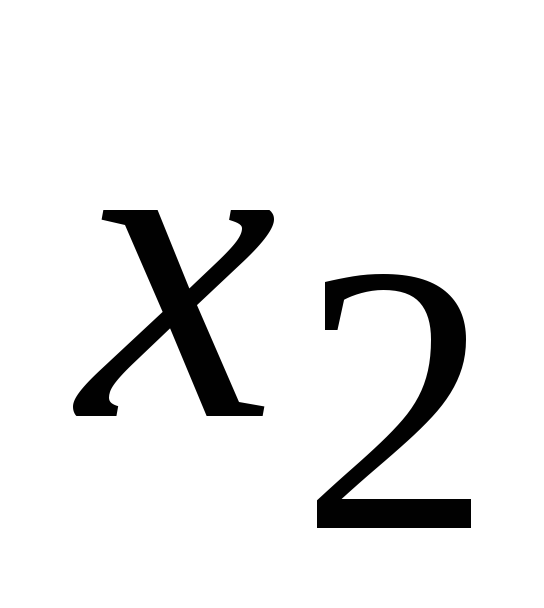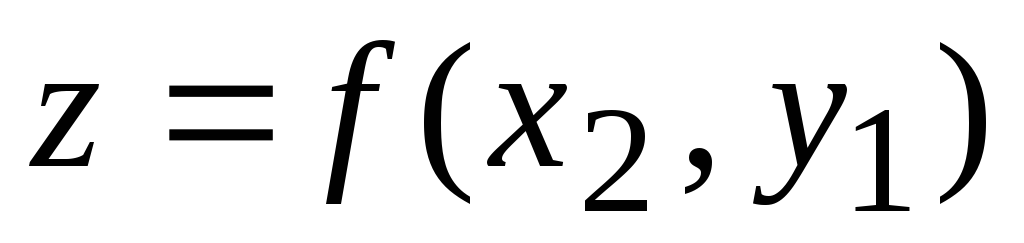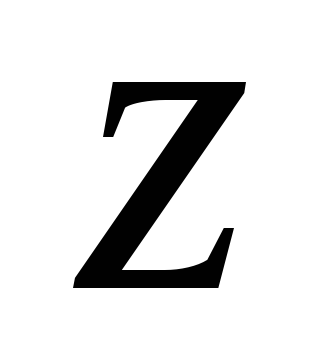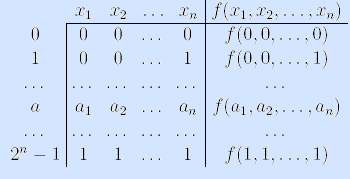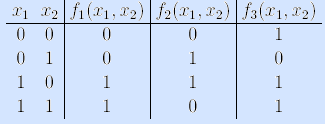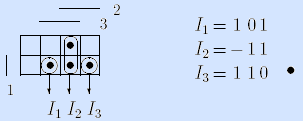Табличный способ задания функции двух переменных

Модуль 2. Дифференциальное исчисление функции нескольких переменных

Тема 1. Функции двух переменных, частные производные,

Определение функций двух переменных.

Способы задания функций двух переменных.

Частные производные высших порядков.

*Дифференциал функции двух переменных и его применение.

*Дифференциал второго порядка

Тема 2. Экстремум функции двух переменных

Условный экстремум функции двух переменных

Тема 3. Наибольшее и наименьшее значения функции двух

Нахождение наибольшего и наименьшего значений функции двух переменных в замкнутой ограниченной области

* Нахождение наибольшего (наименьшего) значений линейной функции в области, заданной линейными ограничениями

Тема 1. Функции двух переменных.

частные производные, дифференциалы, градиент

Определение функций двух переменных.

Способы задания функций двух переменных.

Частные производные высших порядков.

Дифференциал функции двух переменных и его применение.

Дифференциал второго порядка

Определение функций двух переменных

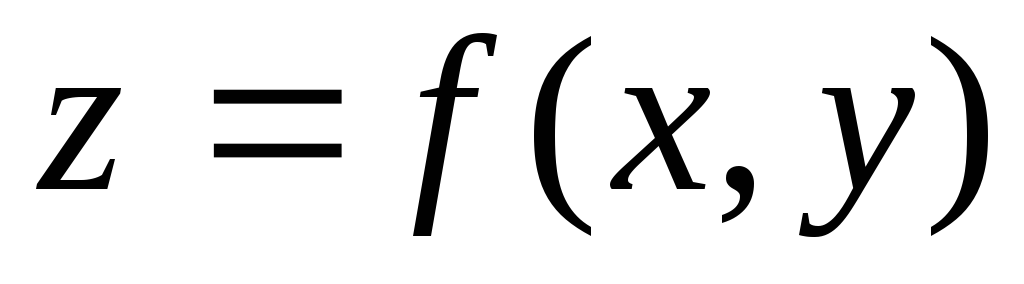
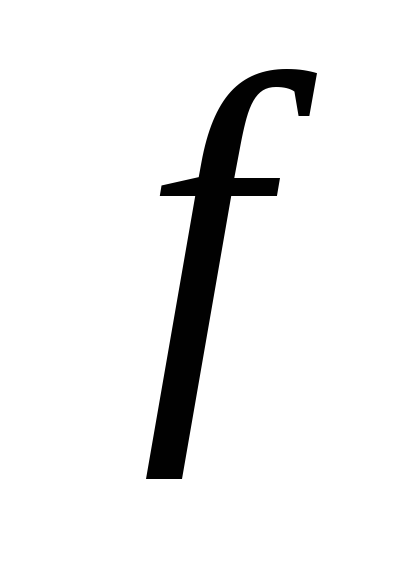
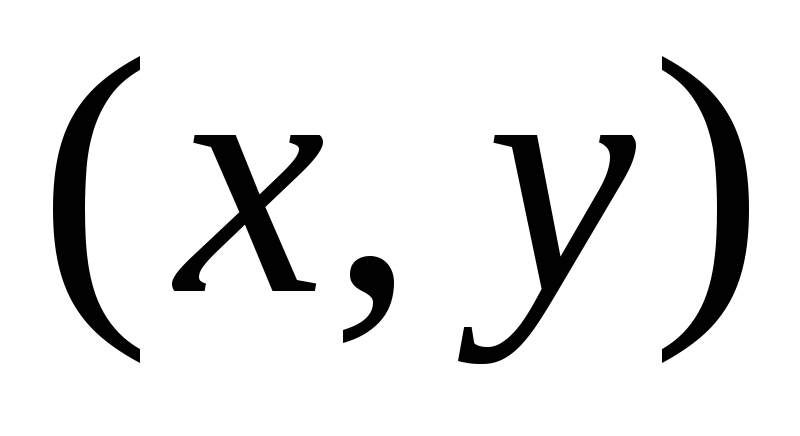
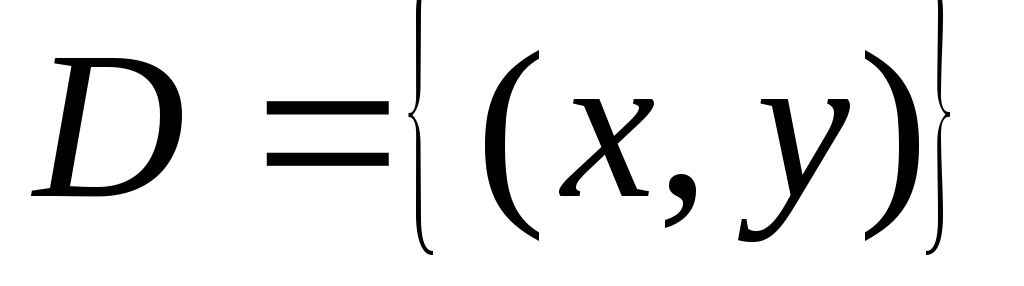
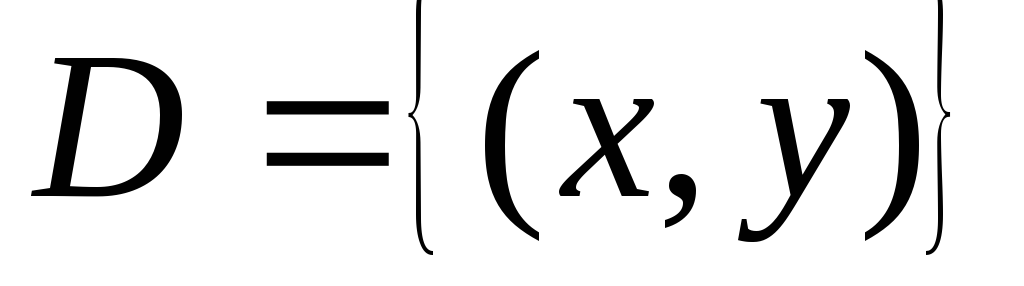
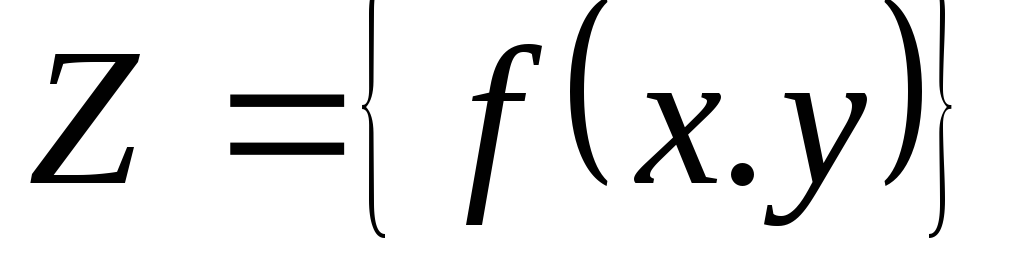
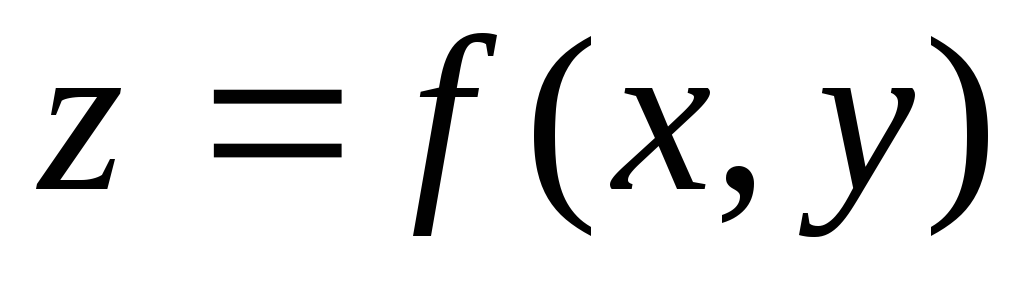
Функцией двух переменных называется правило (закон, соответствие), по которому каждой упорядоченной паре чиселиз некоторого множества на плоскостипоставлено в соответствие единственное числоиз множества. Множествоназываетсяобластью определения, а множество — множеством значений функции .

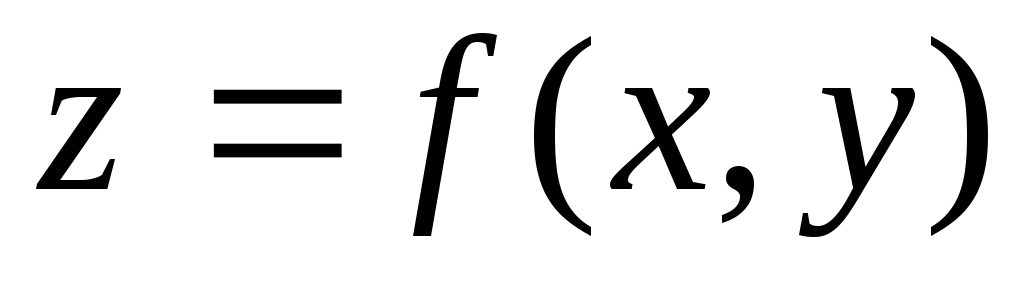
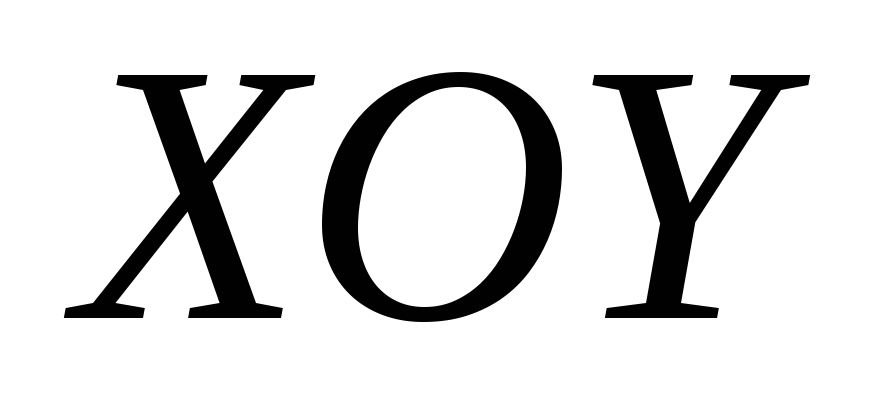
Для функции двух переменных областью определения является некоторое множество точек на плоскости (область), а областью значений — промежуток на оси.

Пример 1. Найти область определения функции .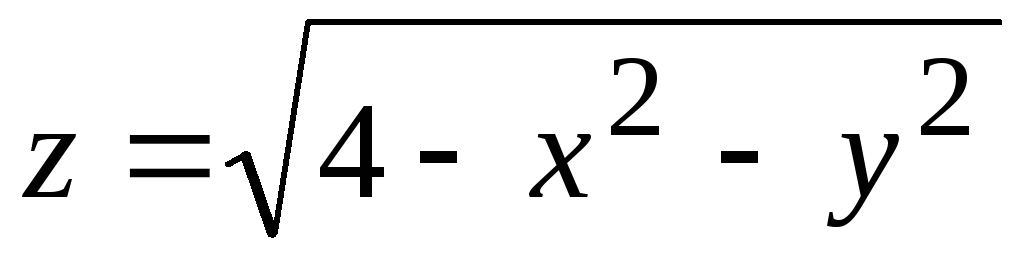

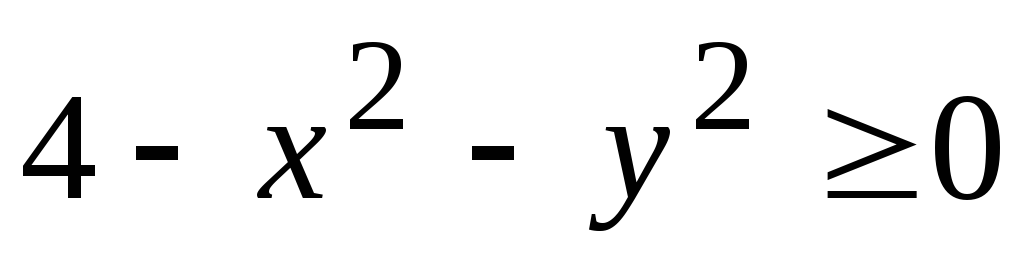
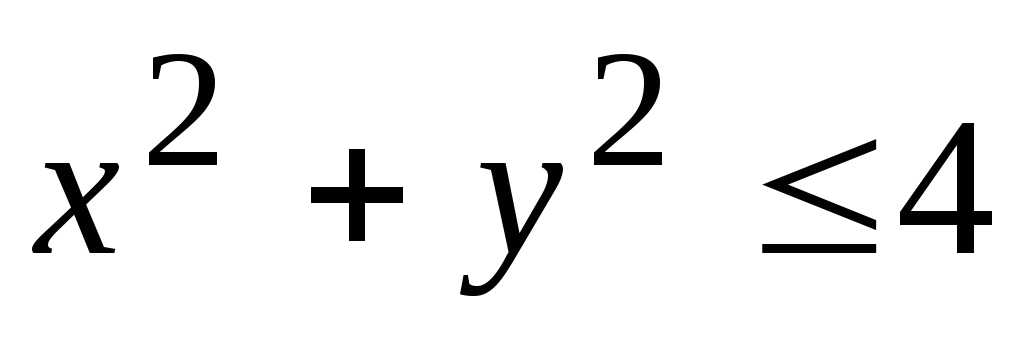
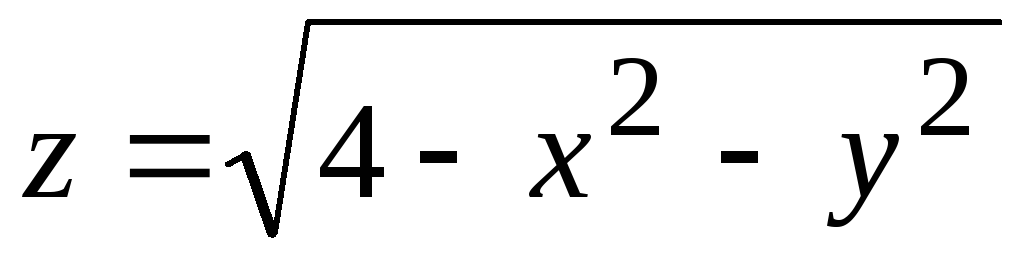
Запишем неравенство . Отсюда. Множество точекна плоскости, координаты которых удовлетворяют полученному неравенству, образуеткруг с центром в начале координат и радиусом . Это и есть область определения функции.

z

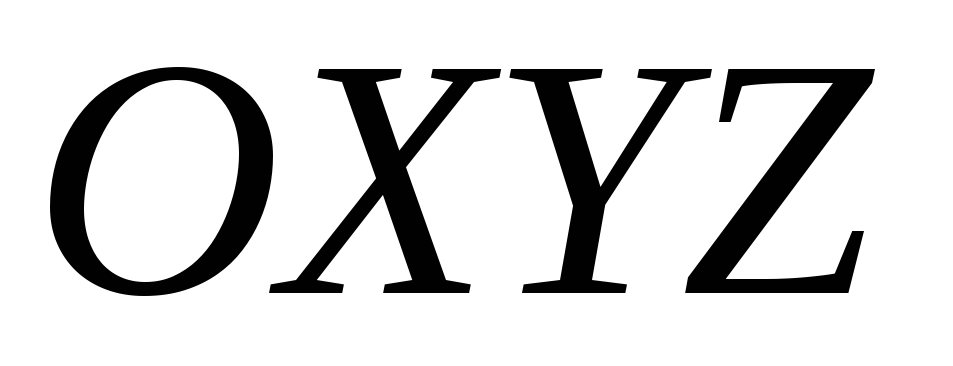
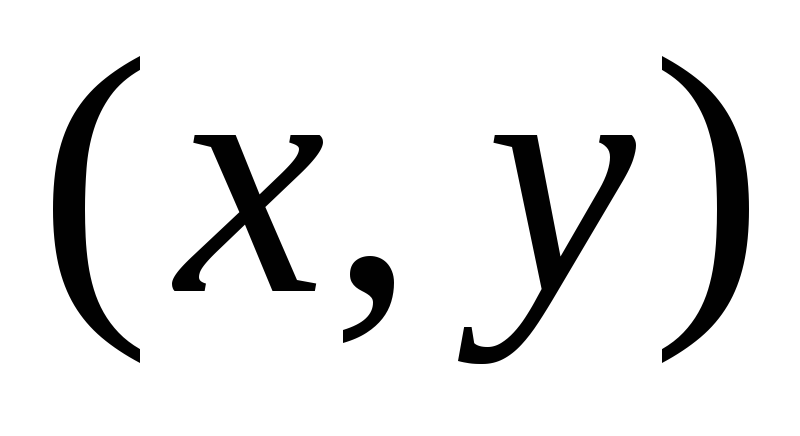
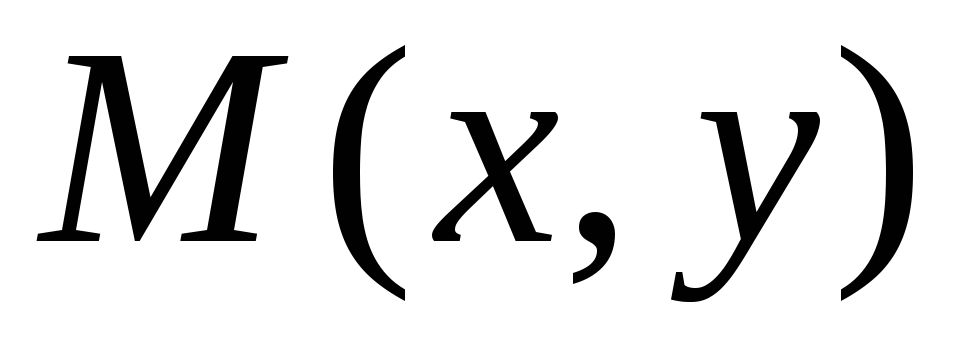
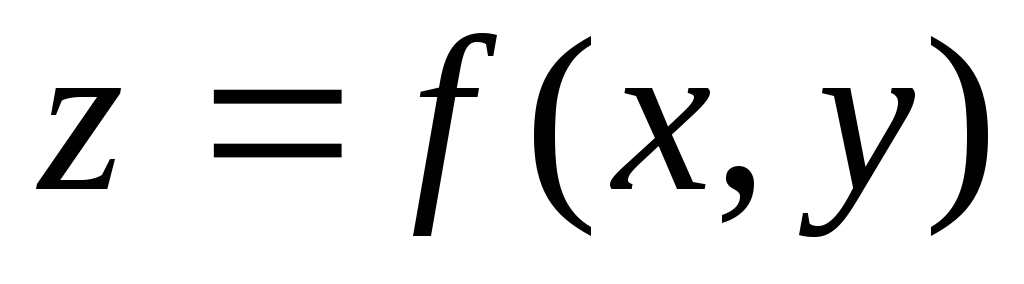
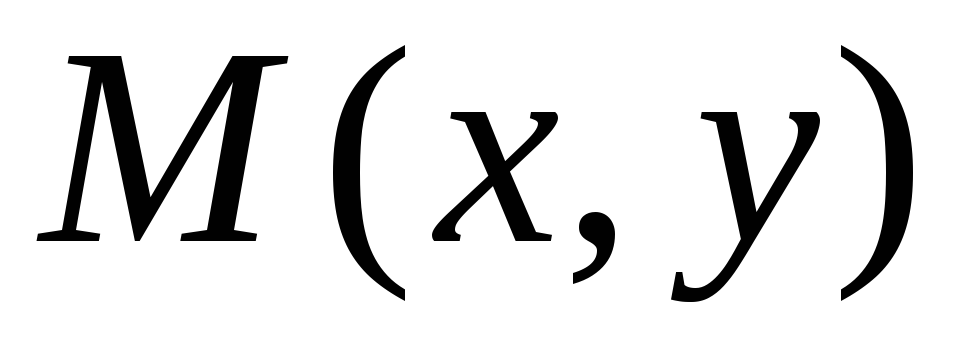
В прямоугольной системе координат каждой упорядоченной паре чиселсоответствует единственная точкакоординатной плоскости, и наоборот. Поэтому функцию двух переменныхудобно рассматривать какфункцию точки и записывать в виде.

2. Способы задания функций двух переменных

Основными способами задания функций являются аналитический, табличный, графический.

Существует и другие способы задания функций — алгоритмический, с помощью программы на ЭВМ.

Аналитический способ задания функции.

одной формулой, разрешенной относительно зависимой переменной (например, 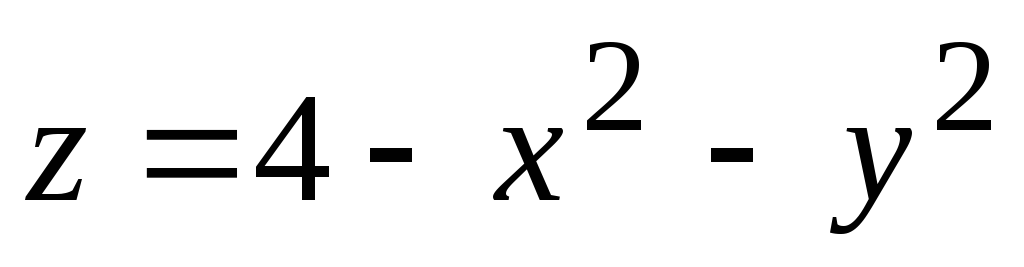), или

разными формулами на определенных числовых промежутках

Функция двух переменных называется неявной, если она задана уравнением, не разрешенной относительно зависимой переменной. Например, .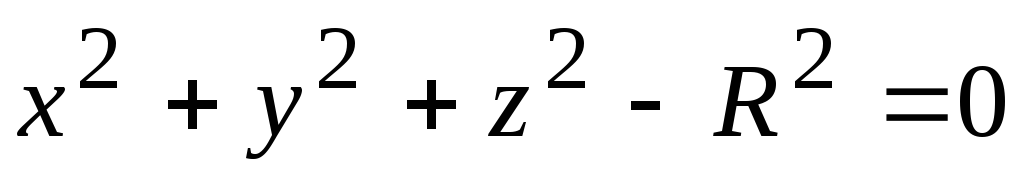

Табличный способ задания функции — с помощью таблицы, в которой указаны значения аргументов и соответствующие им значения зависимой переменной.

Таблица функции двух переменных

Графический способ задания функции.

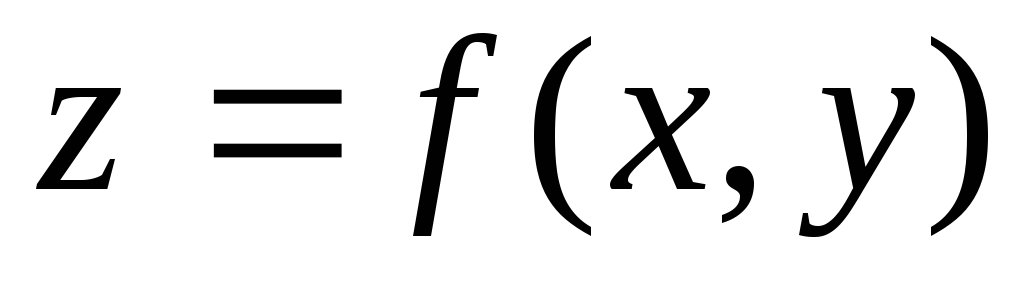
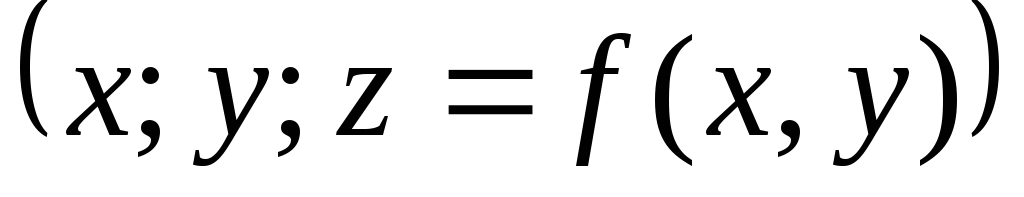
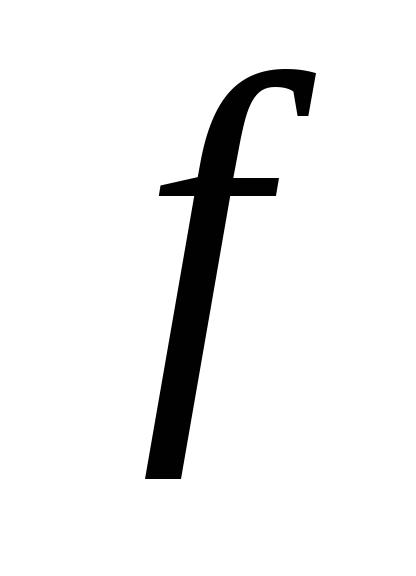
Графиком функции двух переменных являетсяповерхность в трехмерном пространстве ХУZ, состоящая из точек , где парыпринадлежат области определения функции.

Графиком линейной функции является плоскость в пространстве.

Пример 2. Построить график функции .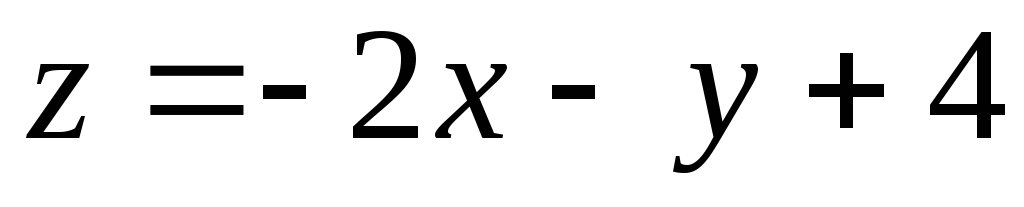

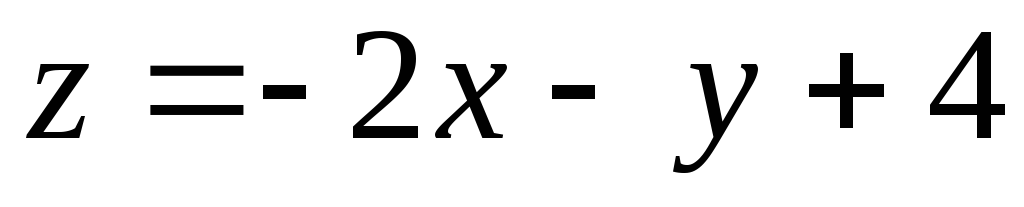
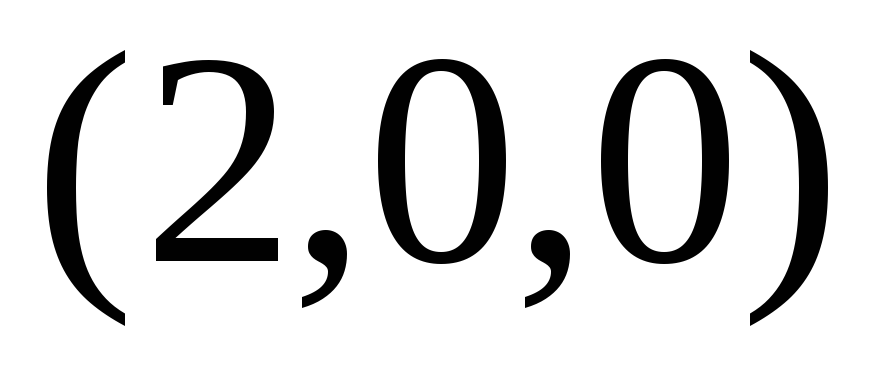
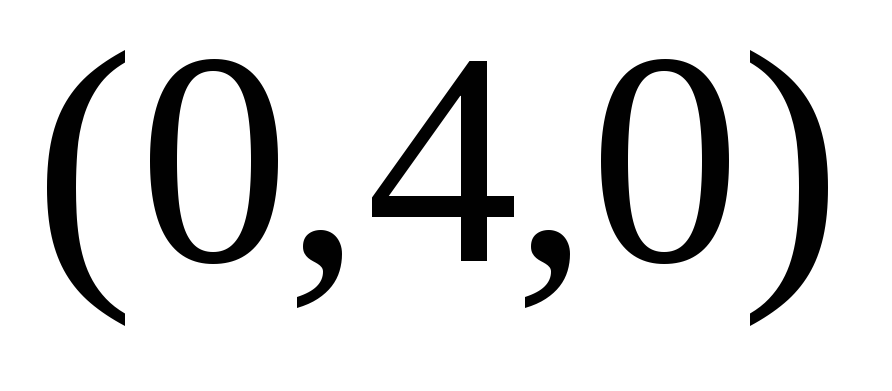
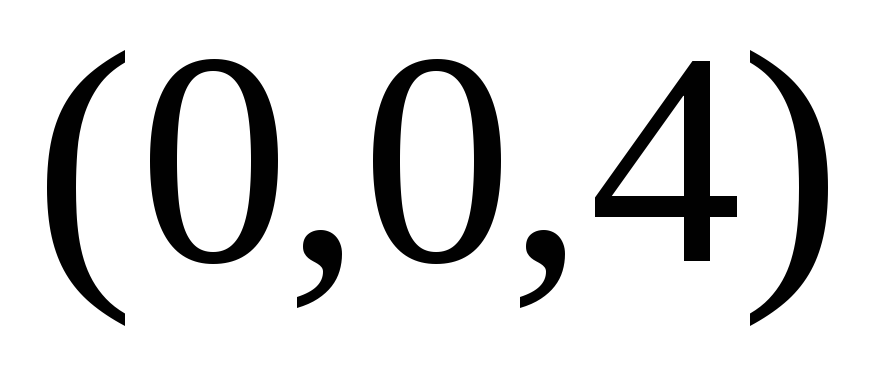
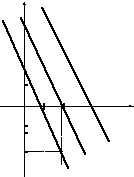
Для функции график представляет собой плоскость, проходящую через точки,,.

4

Одним из способов представления функции двух переменных являются линии уровня.

Линией уровня функции называется линия на плоскости, состоящая из точек области определения, в которых значение функции постоянно, или.

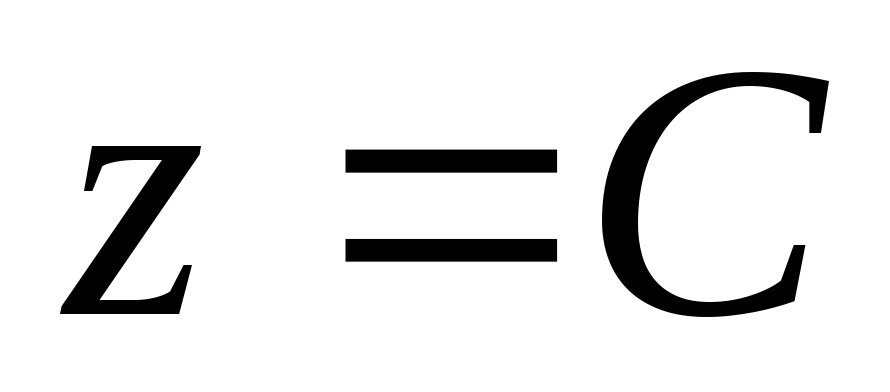
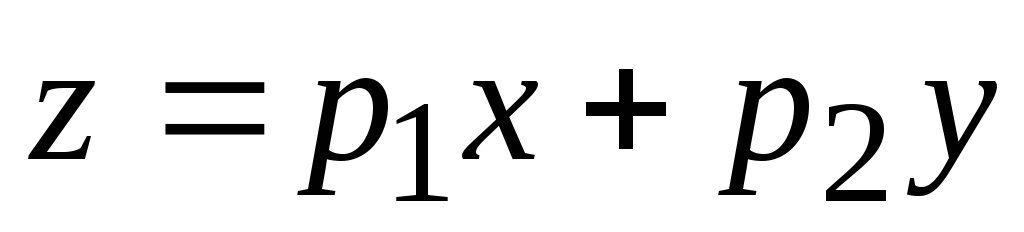
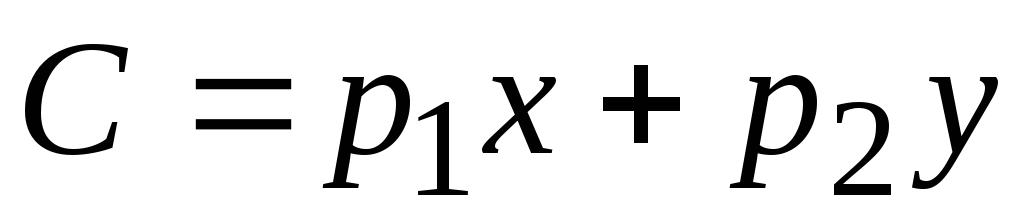
Для линейной функции двух переменных линии уровня задаются уравнениеми представляют собой совокупностьпараллельных прямых на плоскости ХОУ.

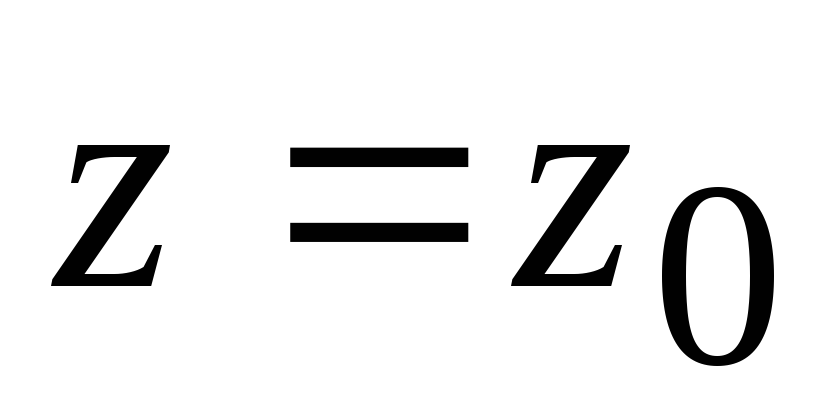
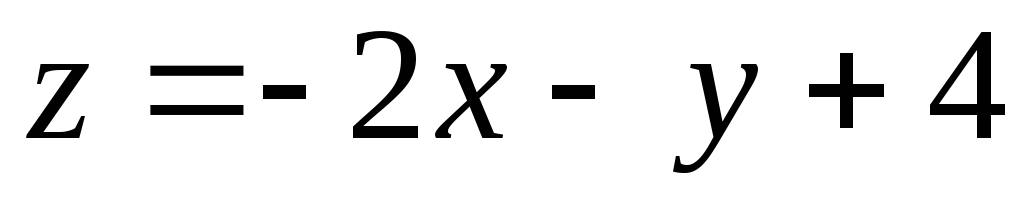
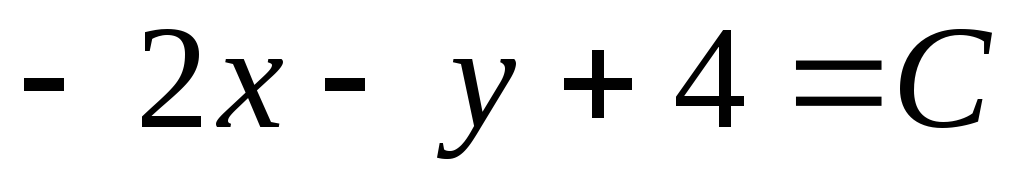
Пример 3. Линиями уровня функцииявляются параллельные прямые, уравнение которых.

Y

Источник

Табличный способ задания функции двух переменных

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f = <α B n :f(α) = 1>;

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f = <α B n :f(α) = 0>.

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

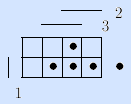
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

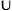
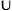
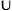
5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = 1, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁ I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = 1, I₂, I₃> интервалов:

Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

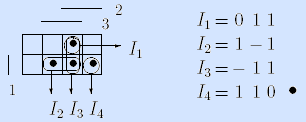
Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = 1, I₂, I₃, I₄> интервалов:

Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

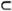
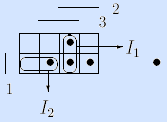
Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I I’.

Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂ 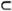I₁.

Пример. Зададим мажоритарную функцию множеством I»_f = 1 I₂, I₃> всех максимальных интервалов.

Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

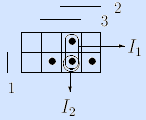
Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Источник