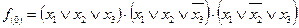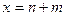Табличный способ задания ФАЛ 3 страница
Обозначения, принятые при изображении логических элементов.
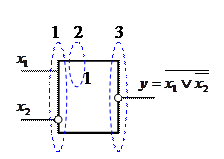
Пусть логический элемент имеет вид, представленный на рис.
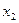
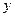
Последовательность преобразования логических сигналов элементом всегда обозначается одинаково. Она следующая:
1) Сначала логические сигналы поступают на входы логического элемента (см. рис. ). Если на входах имеется инверсия, то соответствующие сигналы преобразуются в инверсные (см. рис. пунктирная область №1).
Например, изображённый на рис. элемент имеет инверсию сигнала 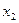
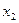
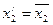
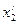
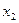 | 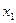 | 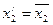 |
Сигнал 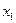
2) Далее с преобразованными сигналами выполняется операция, которая обозначена внутри прямоугольника (см. рис. пунктирная область №2).
Например, представленный на рисунке логический элемент реализует операцию «дизъюнкция» (см. табл. ), причём аргументами для данной операции будут сигналы 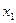
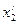
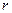
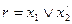
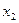 | 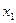 | 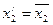 | 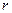 |
При заполнении таблицы используем таблицу истинности элемента «дизъюнкция» (см.табл. ). Поскольку переменная 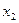
3) Если имеется инверсия на выходе, то результат выполнения предыдущей операции следует инвертировать 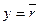
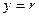
Поскольку в нашем примере имеется инверсия на выходе логического элемента (см. рис. пунктирную область №3), то 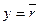
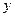
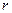
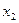 | 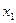 | 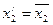 | 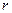 | 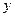 |
4) Так как входными сигналами для изображённого на рисунке логического элемента являются 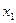
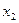
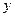
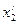
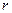
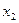 | 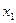 | 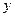 |
Она описывает взаимосвязь между входными сигналами элемента и выходным сигналом.
Теперь, воспользовавшись принципом суперпозиции, выведем аналитическое выражение, задающее ФАЛ элемента, изображённого на рисунке.
В результате преобразования (1) была получена ФАЛ, после преобразования (2) была получена ФАЛ 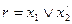
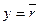
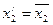
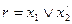
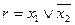
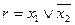
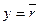
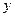
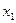
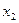
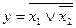
Проанализируем полученную формулу. Формула содержит несколько элементарных преобразований: две инверсии и одну дизъюнкцию. В ней же указан порядок выполнения логических операций, который может быть определен на основе следующих правил:
– Инверсия имеет приоритет перед другими операциями, аналогичный скобкам.
– Инверсия, обозначенная более короткой чертой, имеет приоритет перед инверсией, обозначенной более длинной чертой.
– Инверсия, охватывающая чертой другие логические операции, выполняется после выполнения этих операций.
Для удобства восприятия последовательности операций мысленно выделим части выражения, охваченные чертой соответствующей инверсии парами скобок, это позволит наглядно увидеть в какой последовательности должны выполняться действия в приведенной формуле: 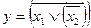
Итак, сначала требуется инвертировать значение переменной 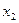
Если сопоставить последовательность аналитических и табличных преобразований, то можно заметить, что она одинакова, а, следовательно, формула 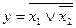
Например, возьмём следующий набор переменных 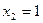
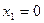
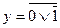
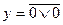
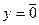
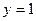
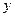
3. набор аргументов, на котором макстерм принимает своё единственное нулевое значение совпадает с набором аргументов, на котором ФАЛ, заданная таблицей истинности (картой Карно), принимает одно из своих нулевых значений.
Задача получения КСНФ может быть разделена на три этапа, аналогичных этапам получения ДСНФ:
– определение количества макстермов;
– определение аналитического выражения для каждого макстерма;
– составление выражения КСНФ.
Определение количества макстермов.
В общем случае КСНФ содержит столько макстермов 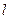
Например, для ФАЛ заданной таблицей истинности (табл.1) при записи КСНФ необходимо использовать три макстерма, т.е.:
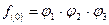
Как видно из сравнения соотношений (20) и (21) количество минтермов и количество макстермов при описании одной и той же ФАЛ в общем случае различно.
Определение аналитического выражения для каждого из макстермов.
Аналитическое выражение для каждого макстерма получают так.
Сначала вводят аналитические выражения для значений переменных, входящих в набор. При этом, если в таблице истинности значение переменной 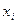
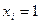
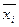
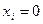
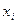
Аналитическое выражение макстерма представляет собой дизъюнкцию (логическое сложение) аналитических выражений значений переменных, входящих в набор, на котором значение макстерма должно быть равно нулю.
Например, макстерм 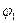
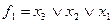
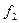
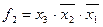
| № набора | 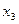 | 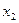 | 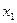 | 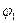 | Комментарий (подстановка значений переменных и вычисление функции) |
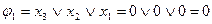 | |||||
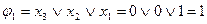 | |||||
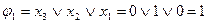 | |||||
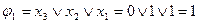 | |||||
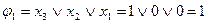 | |||||
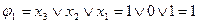 | |||||
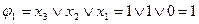 | |||||
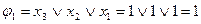 |
Пример построения таблицы истинности:
Рассмотрим последовательность построения таблицы истинности, описывающей функционирование некоторого дискретного устройства,
например, схемы, содержащей три ключа и обмотку реле. Схема их
 |
соединения приведена на рис. 3
а) При построении таблицы истинности в первую очередь необходимо определить количество столбцов в ней. Для этого можно воспользоваться следующей формулой:
где 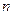
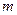
Можно в таблицу истинности добавить ещё один столбец, в который будет служить для нумерации двоичных наборов переменных в десятичной системе, хотя это и не обязательно.
Проанализируем схему (рис. 3). Нетрудно заметить, что состояние обмотки реле 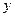
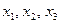
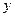
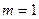
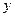
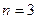
Итак, таблица истинности должна содержать 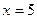
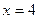
| № набора | 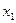 | 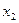 | 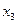 | 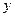 |
б) После того, как определено количество столбцов в таблице истинности ФАЛ, необходимо определить количество строк. Количество строк в таблице равно количеству уникальных (неповторяющихся) наборов переменных, которое можно определить по формуле (1). При этом строка заголовка не учитывается. Поскольку у данной ФАЛ 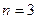
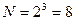
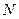
| № набора | 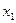 | 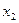 | 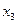 | 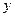 |
в) Теперь необходимо перечислить все уникальные наборы входных переменных ФАЛ. Последовательность заполнения такая. Обычно, сначала заполняется самый правый столбец входных переменных ФАЛ. При этом в соседних двух ячейках столбца чередуют ноль и единицу. Начинают заполнение от нуля, который проставляется в ячейке столбца, расположенной в строке с набором № 0.
г) Остальные столбцы таблицы истинности заполняются таким образом, чтобы в каждом последующем столбце группы ячеек с нулями и единицами были в два раза больше чем в предыдущем. Причем ячейки всех столбцов, относящиеся к строке набора № 0, обязательно заполняют нулями.
| № набора | 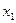 | 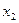 | 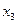 | 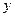 |
 0 0 |
|
|
При правильном заполнении всех столбцов самая верхняя ячейка каждого столбца должна содержать «0», а самая нижняя – «1», причём, в последнем заполненном столбце верхняя половина наборов должна содержать нули, а нижняя – единицы.
д) Далее условимся, что под состоянием любого ключа схемы «0» будем понимать его разомкнутое состояние, то есть состояние, когда он не пропускает ток, а под состоянием «1» – его замкнутое состояние. Аналогично будем считать, что в состоянии «1» обмотка реле 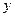
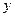
Если 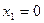
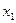
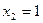
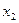
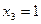
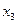
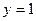
| № набора | 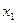 | 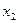 | 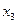 | 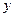 |
Рассуждая аналогичным образом, можно заполнить все остальные ячейки столбца 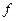
| № набора | 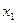 | 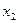 | 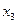 | 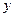 |
Примечание: Если в схеме используются контактные тройники реле, то принято считать, что при включении тройника в схему с использованием фронтового контакта (замыкается, если обмотка реле под током), соответствующая переменная имеет прямое значение 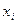
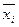
Полученная ФАЛ описывает функционирование только схемы, приведённой на рис. 3. Очевидно, что при иной схеме соединения ключей реле 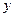
Лекция 3
Минимизация функций алгебры логики
Пусть функционирование некоторой комбинационной схемы описано таблицей истинности. Одной и той же таблице истинности, как правило, могут соответствовать несколько различных аналитических выражений.
Так, например, таблице истинности (табл. 10), соответствуют следующие выражения:
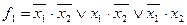
| Таблица 20 | |||
| № набора | 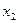 | 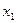 | 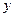 |
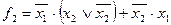
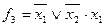
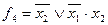
Источник