Табличный способ задания автомата мили

Способы задания автомата (Лекция)

1. Табличный способ

2. Графический способ задания автомата

Чтобы задать конечный автомат S, необходимо описать все элементы множества S = , т.е. необходимо описать входной, выходной алфавиты и алфавит состояний, а также функции переходов d и выходов l . При этом среди множества A = 0,a₁,…, a_n > необходимо выделить начальное состояния a0, в котором автомат находится в момент времени t = 0. Существует несколько способов задания работы автомата, но наиболее часто используются табличный и графический.

При этом способе автомат Мили описывается двумя таблицами: таблицей переходов и таблицей выходов.

Строки этих таблиц соответствуют входным сигналам x ( t ), а столбцы – состояниям. На пересечении столбца a_i и строки x_j в таблице переходов ставится состояние a_s = d [ a_i,x_j ], в которое автомат перейдет из состояния a_i под воздействием сигнала x_j ; а в таблице выходов – соответствующий этому переходу выходной сигнал y_g = l [ a_i,x_j ].

Совмещенная таблица переходов и выходов автомата Мили:

Задание таблиц переходов и выходов полностью описывает работу конечного автомата, поскольку задаются не только сами функции переходов и выходов, но и также все три алфавита: входной, выходной и алфавит состояний.

Для задания автомата Мура требуется одна таблица, поскольку в этом автомате выходной сигнал однозначно определяется состоянием автомата.

Отмеченная таблица переходов автомата Мура :

В этой таблице каждому столбцу приписан, кроме состояния a_i , еще и выходной сигнал y ( t ) = l ( a ( t )), соответствующий этому состоянию. Таблица переходов автомата Мура называется отмеченной потому, что каждое состояние отмечено выходным сигналом.

Приведем примеры табличного задания автоматов Мили и Мура :

По этим таблицам можно найти реакцию автомата на любое входное слово. Например.

Для автомата Мили: Для автомата Мура :

2. Графический способ задания автомата (задание автомата с помощью графа)

Этот способ основан на использовании ориентированных связных графов. Вершины графов соответствуют состояниям автомата, а дуги – переходам между ними. Две вершины графа a_i и a_s соединяются дугой, направленной от a_i к a_s , если в автомате имеется переход из a_i в a_s , т.е. a_s = d ( a_i , x_j ). В автомате Мили дуга отмечается входным сигналом x_j , вызвавшим переход, и выходным сигналом y_g , который возникает при переходе. Внутри кружочка, обозначающего вершину графа, записывается состояние. Например, для автомата Мили, приведенного выше, граф имеет вид а), а для автомата Мура вид б).

Источник

Табличный способ задания автомата

Автомат Мура задается отмеченной таблицей переходов и выходов. Автомат Мили задается либо совмещенной таблицей переходов и выходов, либо двумя таблицами – таблицей переходов и таблицей выходов. Во всех таблицах строки соответствуют входным сигналам, а столбцы – состояниям. Автомат, заданный табличным способом, всегда детерминирован.

В отмеченной таблице переходов автомата Мура каждый столбец отмечается выходным сигналом. Кроме того, на пересечении строки x_i и столбца a_j записывается состояние a_k, в которое перейдет автомат, находящийся в состоянии a_j под действием входного сигнала x_i, т. е. δ(a_j, x_i) = a_k.

Рассмотрим пример табличного задания автомата Мура (табл. 1.1). Пусть автомат Мура имеет три входных сигнала, два выходных сигнала и три состояния.

Отмеченная таблица автомата Мура

y	y1	y2	y1
a x	a0	a1	a2
x1	a1	a1	a0
x2	a0	a2	a1
x3	a2	a0	a2

Данный автомат является полностью определенным.

Рассмотрим пример табличного задания автомата Мили. Пусть автомат Мили имеет два входных сигнала, три выходных сигнала и три состояния.

В клетку таблицы переходов автомата Мили (табл. 1.2) на пересечении строки х_i и столбца a_j записывается состояние, в которое перейдет автомат, а в соответствующую клетку таблицы выходов (табл. 1.3) – выходной сигнал, который автомат выдает на этом переходе.

Таблица 1.2 Таблица переходов автомата Мили δ: (A × X) → A	Таблица 1.3 Таблица выходов автомата Мили λ: (A × X) → Y
а х	а0	а1	а2	а х	а0	а1	а2
х1	а1	а0	а1	х1	y1	y2	–
х2	а0	а2	а1	х2	y1	y3	y2
«–» – значение не определено

Например, δ(а₁, х₁) = а₀ означает, что автомат, находясь в состоянии а₁ при поступлении на вход сигнала х₁, перейдет в состояние а₀; λ(а₁, х₁) = y₂ означает, что автомат, находясь в состоянии а₁ при поступлении на вход сигнала х₁, выдаст выходной сигнал y₂; λ(а₁, х₂) = y₃ означает, что автомат, находясь в состоянии а₁ при поступлении сигнала х₂, выдает выходной сигнал y₃. Таким образом, находясь в одном и том же состоянии, автомат Мили может выдавать различные сигналы.

В этом случае совмещенная таблица переходов и выходов автомата Мили имеет следующий вид (табл. 1.4).

Совмещенная таблица переходов и выходов автомата Мили

а х	а0	а1	а2
x1	а1/y1	а0/y2	а1/–
x2	а0/y1	а2/y3	а1/y2

В клетку совмещенной таблицы переходов и выходов автомата Мили на пересечении строки х_i и столбца a_j записывается состояние, в которое перейдет автомат, а через косую черту – выходной сигнал, который автомат выдает на этом переходе.

Табличный способ обладает невысокой наглядностью, однако автомат, заданный табличным способом, всегда детерминирован. Кроме того, табличное задание автомата позволяет легко перейти к процессу структурного синтеза. Для этого часто используется прямая таблица переходов и выходов автомата.

Рассмотрим пример задания автомата Мура прямой таблицей переходов и выходов. Пусть автомат Мура имеет два входных сигнала, три выходных сигнала и три состояния.

При комбинации (а₁, x₂) не определены функция переходов d = y(а₁) и функция выходов l = j(а₁), см. табл. 1.5.

Прямая таблица переходов и выходов автомата Мура

Исходное состояние аi	Входной сигнал xk	Следующее состояние аj, d = y(аi)	Выходной сигнал yn, l = j(аi)
а0	x1	а1	y1
а0	x2	а0	y1
а1	x1	а2	y3
а1	x2	–	–
а2	x1	а1	y1
а2	x2	а0	y1

В процессе структурного синтеза на основе данной таблицы строится кодированная прямая таблица переходов и выходов автомата (табл. 1.6). При этом столбец 3 будет представлять собой исходные данные для формирования функции возбуждения элементов памяти автомата, имеющей различный вид при реализации памяти автомата на D-триггерах и на JK-триггерах.

Коды состояний в табл. 1.6 представлены в двоичном формате при помощи позиционного двоичного кода с использованием естественного способа кодирования. Входные и выходные сигналы могут быть закодированы в двоичном формате как с использованием унитарного кодирования, так и с использованием кодирования при помощи позиционного двоичного кода.

Прямая кодированная таблица переходов и выходов автомата Мили

Исходное состояние аi	Входной сигнал xk	Следующее состояние аj, d = y(аi)	Выходной сигнал yn, l = j(аi , xk)
а0 (код 00)	x1	а1 (код 01)	y1
а0 (код 00)	x2	а2 (код 10)	y2
а1 (код 01)	x1	а2 (код 10)	y2
а1 (код 01)	x2	–	–
а1 (код 01)	x1	а1 (код 01)	y3
а2 (код 10)	x2	а0 (код 00)	y1

Дата добавления: 2017-09-19 ; просмотров: 1988 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Самостоятельное изучение схемотехники. Абстрактный автомат. Часть 2

Статья написана, собрана и сверстана Brotherofken. Спасибо ему огромное.
В предыдущей статье я попытался изложить все основные определения и принципы, чтобы сделать эту статью максимально понятной. Все не уместилось, так что я настоятельно советую ознакомиться с этими файлами:
Базис, Базис2, Минимизация. Далее в этой статье я оставил несколько разъясняющих пометок курсивом.

В этой статье я попробую объяснить доступным языком что такое абстрактный автомат, способы его представления. Так как теория автоматов полна математики и сложна, постараюсь писать человеческим языком, чтобы неподготовленный читатель смог понять о чём идёт речь.

Электронные цифровые схемы формально можно разделить на 2 класса:

• Комбинационные Схемы (КС) – не обладают памятью. Выходной сигнал формируется в зависимости от комбинации входных данных в фиксированный момент времени (учитывая задержку на преобразования сигналов).Комбинационные схемы, их типы и принципы построения могут быть темой для отдельной статьи, а в качестве примеров можно привести: Управляемые шины, мультиплексоры и демультиплексоры, дешифраторы и шифраторы, преобразователи кодов, комбинационные счетчики и сумматоры и т. д.
• Схемы с памятью – алгоритм их работы зависит от состояния входов и памяти (того, что было в предыдущие моменты времени). Эти схемы описываются с применением теории конечных автоматов. Речь о них и пойдёт далее.

Другими словами первый класс — логические устройства, обрабатывающие входной сигнал. Второй элементы обладающие памятью и реагирующие на сигнал в зависимости от введенных в них данных.

Абстрактный автомат

Автомат должен будет реализовывать некоторые функции, которые заданы разработчиком. Он может быть простым сумматором, может реализовывать какую-либо микрокоманду процессора, выбирать слова из оперативной памяти или заниматься синтаксическим анализом выражения.
В общем виде, не вдаваясь в подробности, абстрактный автомат можно представить следующим образом:

Или, если перейти от иллюстрации к математическому описанию:
A =

Такой автомат функционирует дискретно по времени, то есть значения входов, выходов и внутреннее состояние автомата изменяются в дискретные моменты времени.
Итак мы в общем виде описали что есть Абстрактный автомат. Примером такого автомата может быть триггер, регистр ЭВМ или сумматор.

Выделяют 2 типа автоматов:

1. Автоматы Мили. Описывается системой уравнений:
   c(t) = δ( a(t), c(t-1) );
   b(t) = λ( a(t), c(t-1) ).
2. Автоматы Мура. Описывается уравнениями:
   c(t) = δ( a(t), c(t-1) );
   b(t) = λ( a(t), c(t) ).

Как видно состояние автомата c(t) в текущий момент времени является функцией его состояния в предыдущий момент времени и входного сигнала.
Отличаются автоматы видом функции выхода. В автомате Мили выходной сигнал определяется входным сигналом a(t) и состоянием автомата в предыдущий момент времени c(t-1). Выходной сигнал автомата Мура определяется парой входного сигнала a(t) и состояния в данный момент c(t).
Так же можно отметить, что от одного типа можно перейти ко второму и наоборот, причем при переходе от автомата Мили к автомату Мура число внутренних состояний автомата останется прежним, а при обратном переходе число внутренних состояний может возрасти. На этом останавливаться подробно не будем, считая, что синтезировали(нарисовали граф) автомат того типа, который надо.
Итак, на этом с матчастью окончено. Попробуем описать автоматы.

Т.е. автомат типа Мили вырабатывает выходной сигнал когда у него меняется входной, в зависимости от его предыдущего состояния. При этом длительность выходного сигнала не зависит от длительности входного, а только от его присутствия. В автоматах типа Мура выходной сигнал зависит от состояния автомата в текущий момент времени т.е. автомат будет вырабатывать определенный выходной сигнал пока не изменит свое состояние.

Способы задания автоматов

Как мы выяснили в первой части — автомат представляет собой совокупность входного и выходного алфавитов, множества внутренних состояний и функций, определяющих переходы и выходы. Однако, обычно функции δ и λ не заданы, и поведение автомата приходится описывать по-другому.

Есть два основных способа задания автомата:

1. При помощи графов.
2. При помощи таблиц переходов и выходов.

Графы

Граф автомата – это ориентированный связный граф, вершины которого символизируют внутренние состояния автомата, а дуги – переходы из одного состояния в другое.

Для графа Мили на дугах указываются сходные и выходные буквы. Выходные буквы пишутся над дугами, символизируя то, что выходное состояние зависит от состояния автомата в предыдущий момент времени.

Для графа автомата Мура на дугах записываются только входные буквы, выходные же указываются около вершин.

Важный момент: Если из каждой вершины выходит столько дуг, сколько есть входных букв, то автомат называется полным. Другими словами – если из каждой вершины определены переходы для каждой входной буквы. В наших примерах автомат Мили является полным, а автомат Мура – частичным.
И ещё: Если из одной вершины выходит дуг больше, чем входных букв (то есть 2 и более дуг с одинаковыми входными буквами), то такой автомат называется недетерминированным. Такое может произойти при построении формализованного описания и тогда надо будет произвести переход к детерминированному автомату, но это не всегда можно выполнить. Описание этого процесса я тоже упускаю, сразу нарисовав детерминированный автомат.
На этом о графах всё.

Таблицы переходов и выходов.

Графы нагляднее для человека, а таблицы — для машины. Любой автомат можно представить в виде таблицы переходов и выходов (ТПВ). В ТПВ строками являются внутренние состояния автомата, а столбцами – входные буквы.
Построим ТПВ для наших графов Мили и Мура. Если не определена какая-либо входная или выходная буква, то вместо неё ставится прочерк. Если не определено состояние, то действует это же простое правило.

ТПВ графа Мили

В ТПВ Мили в каждой клетке записаны переходы и выходы. Например, если автомат находится в состоянии С0 и на вход приходит буква a1, то он перейдёт в состояние С1 и на выходе появится буква b3.

ТПВ графа Мура

Для графа Мура строят отмеченную таблицу переходов. Выделяется дополнительный столбец для выходных букв.
В клетке под входной буквой пишется в какое состояние автомат переходит, в крайней правой клетке — какую выходную букву возвращает.

Пример синтеза автомата

При помощи абстрактных автоматов можно описать практически что угодно. Можно описать работу цифровой схемы, а можно – синтаксический или лексический анализатор. Попробуем описать триггер – чем не автомат?
Чтобы задать граф нужно словесное описание алгоритма работы триггера. Читаем:

Кодируем входной и выходной алфавиты:
A = , где a0 – логическая 1 на входе R, a1 – логическая единица на входе S.
B = , где b0 – логический 0 на выходе Q, b1 – логическая единица на выходе Q.
Строим граф автомата Мили:

Вот такая забавная чебурашка получилась :-). Теперь можно построить таблицу переходов и выходов:

Если расписать эту таблицу преобразовав условные обозначения в фактические, то получим таблицу которая представляет из себя таблицу переходов триггера. Затем её можно упростить:

Нанесём полученную функцию на карту Вейча и минимизируем:

Выпишем, что получилось:

Строим по функции схему (Выполняли домашнее задание?):

Немного непривычно видеть триггер в булевом базисе, поэтому переведём функцию в базис И-НЕ и нарисуем схему в нём:

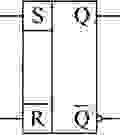
А на схеме асинхронный RS триггер обозначается вот так:

Теперь если приложить немного старания, то можно самостоятельно синтезировать простую новогоднюю гирлянду.

Источник