Методы решения комбинаторных задач
Методы решения комбинаторных задач
Перебор возможных вариантов
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?
Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.
Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.
Ответ:
Вариант1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант6: 1) Громов, 2) Иванов, 3) Орлов.
Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Ответ:
1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег.
Дерево возможных вариантов
Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.
Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?
Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
Задача 5.
Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап — на байдарках, велосипедах или пешком. И третий этап пути — пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?
Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе — А, на байдарках — Б, велосипедах — В, пешком — Х, на канатной дороге — К.
Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.
Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.
Решение. Построим дерево возможных вариантов, обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура.
Ответ: Всего 24 возможных варианта:
Источник
Элементы комбинаторики. Методы решения некоторых задач
Разделы: Математика
1) Немного истории.
В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: устанавливать их связь между элементами каждого, определять число множеств или их подмножеств, обладающих заданным свойством. Такие задачи приходится рассматривать при определении наиболее выгодных коммуникаций внутри города, при организации автоматической телефонной связи, работы морских портов, при выявлении связей внутри сложных молекул, генетического кода, а также в лингвистике, в автоматической системе управления, значит и в теории вероятностей, и в математической статистике со всеми их многочисленными приложениями.
Поговорим об одном из разделов теории вероятности – комбинаторике.
Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики.
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов — во время работы.
Комбинаторные навыки оказались полезными и в часы досуга. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника.
Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18 веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557), Г.Галилею (1564-1642) и французс- ким ученым Б.Паскалю (1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе “ Об искусстве комбинаторики ”, опубликованной в 1666 году. Он также впервые ввел термин “комбинаторика”. Значительный вклад в развитие комбинаторики внес Л.Эйлер. В современном обществе с развитием вычислительной техники комбинаторика “добилась” новых успехов. В настоящее время в образовательный стандарт по математике включены основы комбинаторики, решение комбинаторных задач методом перебора, составлением дерева вариантов (еще его называют “дерево возможностей”) с применением правила умножения. Так, например, “дерево возможностей” помогает решать разнообразные задачи, касающиеся перебора вариантов происходящих событий. Каждый путь по этому “дереву” соответствует одному из способов выбора, число способов выбора равно числу точек в нижнем ряду “дерева”. Правило умножения заключается в том, что для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В. В задачах по комбинаторике часто применяется такое понятие как факториал (в переводе с английского “factor” — “множитель”).
Итак, произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут: n!=1 2 3 … (n-1) n
В комбинаторике решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
2) ЗАДАЧИ
1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе — мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье — чай и компот. Сколько различных обедов можно составить из указанных блюд?
1 способ. Перечислим возможные варианты
Источник
Решение комбинаторных задач

Краткий конспект по теме: Решение комбинаторных задач
Просмотр содержимого документа
«Решение комбинаторных задач»
Тема урока: Решение комбинаторных задач
Методы решения комбинаторных задач:
метод перебора (подбираются задачи на развитие мышления);
табличный метод (все условия вносятся в таблицу, в ней же выполняется решение);
построение дерева возможных вариантов решений;
Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?
Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.
Задача 2. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.
Задача 3. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). сколько различных вариантов завтрака можно составить?
Ответ: 9 вариантов.
Метод построения дерева возможных вариантов решений
Подбирая различные комбинации, можно запутаться. В этом случае приходит на помощь метод построения дерева возможных вариантов решений. Внешне такая схема напоминает дерево, отсюда и название.
Если его правильно построить, ты не упустишь ни один из возможных вариантов решения.
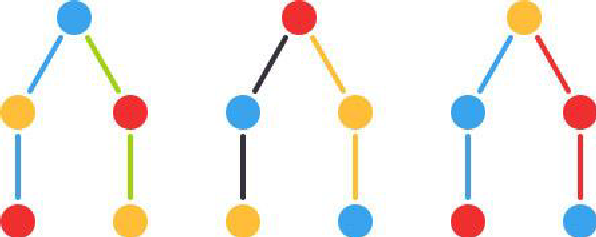
Рассмотрим задачу 1. Учитель попросил Олега разложить на полке 3 шара — желтый, красный, синий. Сколькими способами Олег может это сделать?
Начать можно и с желтого, и с красного, и с синего шара. Дерево вариантов будет выглядеть так:
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Каждый первый шар — это «корень» дерева, а ветви дерева — это различные варианты расположения шаров. По этой схеме несложно посчитать, что возможных комбинаций всего 6.
Ответ: 6 способов.
Схему-дерево возможных рассуждений можно располагать по-разному (корень вверху или внизу).
Применяется для нахождения числа всех возможных исходов независимого проведения двух испытаний А и В, перемножив число всех исходов испытания А и число всех исходов испытания В.
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
Первую цифру выбираем четырьмя способами (1, 2, 5, 8), вторую цифру можно выбрать тремя способами, и на выбор третьей цифры остается два способа. Количество искомых трехзначных чисел равно произведению 4 · 3 · 2 = 24.
В финальном забеге на 100 м участвуют Смирнов, Петров и Орлов. Назовите возможные варианты распределения призовых мест. (Решить, используя табличный метод)
В столовой предлагают два первых блюда: щи и борщ; три вторых блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
Источник
Комбинаторика. Классические алгоритмы решения комбинаторных задач
Выбранный для просмотра документ Комбинаторика.pptx
Описание презентации по отдельным слайдам:
Комбинаторика. Классические алгоритмы решения комбинаторных задач Карандаева А.В. МДИ-113
«Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься»
КОМБИНАТОРИКА – это раздел математики, посвященный задаче выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами.
Классические алгоритмы (методы) решения комбинаторных задач Метод перебора возможных вариантов; Табличный метод; Построение дерева возможных вариантов решений; Построение граф-схемы.
Метод перебора возможных вариантов Задача 1. Для своих двух книг Маша купила три разные обложки. Сколькими различными способами она может обернуть книги купленными обложками? Ответ: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.
Задача 2. Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5? Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55. Метод перебора возможных вариантов
Задача 3. В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест. Ответ: Вариант 1: 1. Иванов, 2. Громов, 3. Орлов. Вариант 2: 1. Иванов, 2. Орлов, 3. Громов. Вариант 3: 1. Орлов, 2. Иванов, 3. Громов. Вариант 4: 1. Орлов, 2. Громов, 3. Иванов. Вариант 5: 1. Громов, 2. Орлов, 3. Иванов. Вариант 6: 1. Громов, 2. Иванов, 3. Орлов. Метод перебора возможных вариантов
Табличный метод Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9? Решение: Составим таблицу: слева первый столбец – первые цифры искомых чисел, вверху первая строка – вторые цифры. Ответ: 28. 1 3 7 9 1 11 13 17 19 3 31 33 37 39 4 41 43 47 49 6 61 63 67 69 7 71 73 77 79 8 81 83 87 89 9 91 93 97 99
Задача 2. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). Сколько различных вариантов завтрака можно составить? Решение: Ответ: 9 вариантов. Табличный метод П К Б С СП СК СБ Ч ЧП ЧК ЧБ М МП МК МБ
Метод построения дерева возможных вариантов решений Задача 1. Учитель попросил Олега разложить на полке 3 волшебных шара – желтый, красный, синий. Сколькими способами Олег может это сделать? Ответ: 6 способами.
Задача 2. Катя собирается на каникулы. Она может поехать с бабушкой или с родителями. Если Катя поедет с бабушкой, то она сможет провести каникулы или на даче, или в городе, или в деревне. Если она поедет с родителями, то она сможет провести каникулы или отдыхая в санатории, или путешествии по горам, или путешествуя на теплоходе. Сколько разных вариантов есть у Кати, чтобы провести свои каникулы? Метод построения дерева возможных вариантов решений
Каникулы Кати Бабушка Родители Дача Город Деревня Санаторий Горы Теплоход Ответ: 6 вариантов
Метод построения граф-схемы Задача 1. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно? Ответ: сыграно 6 партий А Б Г В
Задача 2. Вася, Коля, Петя, Аня и Наташа – лучшие лыжники в пятом классе. Для участия в соревнованиях нужно выбрать из них одного мальчика и одну девочку. Сколькими способами это можно сделать? Ответ: 6 способов. Метод построения граф-схемы В К А Н П
Выбранный для просмотра документ Реферат.docx
«Комбинаторика. Классические алгоритмы решения комбинаторных задач»
1 Определение комбинаторики…..…………..……………………………….
2 Методы решения комбинаторных задач.……………….………………….
2.1 Метод перебора возможных вариантов….…………………..….………..
2.3 Метод построения дерева возможных вариантов………………………..
2.4 Метод построения граф-схемы……………………………………………
Список использованных источников………………………………………….
В обычной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор возможных вариантов или подсчитать их число. Задачи, требующие такого решения, называются комбинаторными. Раздел математики, в котором изучают комбинаторные задачи, называют комбинаторикой.
Комбинаторика – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного множества в соответствии с заданными правилами.
Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией. Поэтому можно сказать, что целью комбинаторного анализа является изучение комбинаторных конфигураций. Это изучение включает в себя вопросы существования комбинаторных конфигураций, алгоритмы их построения, оптимизацию таких алгоритмов, а также решение задач перечисления, в частности определение числа конфигураций данного класса. Простейшим примером комбинаторных конфигураций являются перестановки, сочетания и размещения.
Большой вклад в систематическое развитие комбинаторных методов был сделан Г. Лейбницем (диссертация «Комбинаторное искусство»), Я. Бернулли (работа «Искусство предположений»), Л. Эйлером. Можно считать, что с появлением работ Я. Бернулли и Г. Лейбница комбинаторные методы выделились в самостоятельную часть математики.
Возвращение интереса к комбинаторному анализу относится к 50-м годам ХХ в. в связи с бурным развитием кибернетики и дискретной математики и широким использованием электронно-вычислительной техники. В этот период активизировался интерес к классическим комбинаторным задачам.
Классические комбинаторные задачи – это задачи выбора и расположения элементов конечного множества, имеющие в качестве исходной некоторую формулировку развлекательного содержания типа головоломок.
Существуют такие классические алгоритмы (методы) решения комбинаторных задач, как метод перебора возможных вариантов, табличный метод, построение дерева возможных вариантов решений, построение граф-схемы.
1 Определение комбинаторики
В сказках, старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. С какой проблемой сталкивается добрый молодец на перепутье? Конечно, с проблемой выбора дальнейшего пути движения.
А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был наилучшим.
Оказывается, существует целый раздел математики, именуемый комбинаторикой, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать оптимальную. Комбинаторика позволяет ответить на вопросы: сколькими способами, сколько вариантов и так далее. Слово «комбинаторика» происходит от латинского слова combinare, которое означает «соединять, сочетать». Можно научить маленького человека считать, как счетная машина, проштудировать с ним горы энциклопедий. И это будет только определѐнное количество информации, которой ребенок не сумеет воспользоваться. Гораздо важнее воспитать его мышление так, чтобы он сам сумел находить и отбирать нужную информацию. Вот комбинаторика и формирует такие качества мышления, как системность, вариативность, гибкость. Все эти качества характеризуют комбинаторный стиль мышления.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации, подчинѐнные тем или другим условиям, из заданных объектов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач. Решение комбинаторных задач таит в себе большие развивающие возможности: на их основе совершенствуются приемы умственной деятельности, формируется важная для человека способность комбинировать. Задачи по комбинаторике включают в математические олимпиады и конкурсы.
Комбинаторика возникла в XVI веке и первоначально в ней рассматривались комбинаторные задачи, связанные в основном с азартными играми. В карты и кости выигрывались золото и бриллианты, дворцы, породистые кони и дорогие украшения.
Широко были распространены всевозможные лотереи. Одним из первых занялся подсчетом числа возможных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывающую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами.
Вот одна из комбинаторных задач: У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у двух других – пятидесятирублевые. Билет в кино стоит 50 рублей. В начале продажи касса пуста. Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи?
Можно найти два варианта решения:
1) 50 рублей, 100 рублей, 50 рублей, 100 рублей;
2) 50 рублей, 50 рублей, 100 рублей, 100 рублей.
При решении комбинаторных задач можно использовать разные методы.
2 Методы решения комбинаторных задач
Существуют такие методы решения комбинаторных задач, как:
метод перебора (подбираются задачи на развитие мышления);
табличный метод (все условия вносятся в таблицу, в ней же выполняется решение);
построение дерева возможных вариантов решений;
2.1. Метод перебора возможных вариантов
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
Способ перебора может применяться в простых задачах, например в таких, как эта:
Задача 1. Для своих двух книг Маша купила три разные обложки. Сколькими различными способами она может обернуть книги купленными обложками?
Ответ: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.
Задача 2. Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?
Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.
Задача 3. В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.
Задача 4. В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?
Ответ: 1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег. А теперь рассмотрим варианты организованного перебора.
2.2 Табличный метод
Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?
Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.
Задача 2. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.
Задача 3. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). сколько различных вариантов завтрака можно составить?
Ответ: 9 вариантов.
2.3. Метод построения дерева возможных вариантов решений
Подбирая различные комбинации, можно запутаться. В этом случае приходит на помощь метод построения дерева возможных вариантов решений. Внешне такая схема напоминает дерево, отсюда и название.
Если его правильно построить, ты не упустишь ни один из возможных вариантов решения.
Рассмотрим задачу 1. Учитель попросил Олега разложить на полке 3 волшебных шара — жѐлтый, красный, синий. Сколькими способами Олег может это сделать?
Начать можно и с жѐлтого, и с красного, и с синего шара. Дерево вариантов будет выглядеть так:
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Каждый первый шар — это «корень» дерева, а ветви дерева — это различные варианты расположения шаров. По этой схеме несложно посчитать, что возможных комбинаций всего 6.
Схему-дерево возможных рассуждений можно располагать по-разному (корень вверху или внизу).
Задача 2. Катя собирается на каникулы. Она может поехать с бабушкой или с родителями. Если Катя поедет с бабушкой, то она сможет провести каникулы или на даче, или в городе, или в деревне. Если она поедет с родителями, то она сможет провести каникулы или отдыхая в санатории, или путешествия по горам, или путешествуя на теплоходе. Сколько разных вариантов есть у Кати, чтобы провести свои каникулы?
ВСЕГО: 6 вариантов
2.4. Метод построения граф-схемы
Все видели схему станций метрополитена, трамвайных путей или карту железнодорожных сообщений. Точки — города, отрезки или дуги, которые их соединяют — железнодорожные пути. Такие схемы и называют графами.
Итак, если произвольные точки пространства соединены между собой отрезками или дугами (не обязательно все), то такое соединение (схема) называется графом.
Граф – это набор точек, некоторые из которых соединены линиями.
Эти точки называются вершинами. Соединяющие их линии называются
ребрами графа. Граф – это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рѐбра графа). При этом с помощью вершин изображают элементы некоторого множества (предметов, людей и т.д.), а с помощью рѐбер — определѐнные связи между элементами. Для удобства иллюстрации условия задачи, вершины графа могут быть заменены кругами или прямоугольниками.
Задача 1. В парке 4 пруда. Было решено засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т.е. не нужно было идти в обход. Задание: покажи, какие дорожки надо сделать.
Это пример полного графа
Ответ: 6 дорожек
Задача 2. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Ответ: сыграно 6 партий
Задача 3. Вася, Коля, Петя, Аня и Наташа — лучшие лыжники в пятом классе. Для участия в соревнованиях нужно выбрать из них одного мальчика и одну девочку. Сколькими способами это можно сделать?
Решение: Эту задачу можно решить с помощью следующей схемы.
Ответ: 6 способов.
Итак, комбинаторика изучает, сколько различных комбинаций можно составить из данных объектов по определѐнным правилам.
Комбинаторика – это большой и важный раздел математики, изучающий множества целых чисел и перестановки внутри этих множеств.
Задачу можно назвать комбинаторной, если ее решением является перебор элементов некоторого конечного множества.
Особая примета комбинаторных задач – вопрос, который можно сформулировать, таким образом, что он начинался бы словами:
Для того чтобы решить задачу по комбинаторике, необходимо сначала понять её смысл, то есть, представить мысленно процесс или действие, описанное в задаче.
Список использованных источников
Виленкин, Н. Я. Комбинаторика / Н. Я. Виленкин. – М. : Наука, 1969. – 328 с.
Егоров, А. А. Логика и комбинаторика / А. А. Егоров. – М. : Бюро Квантум, 2002. – 127 с.
Ежов, И. И. Элементы комбинаторики / И. И. Ежов. – М. : Наука, 1977. – 80 с.
Сачков, В. Н. Введение в комбинаторные методы дискретной математики / В. Н. Сачков. – М. : МЦНМО, 2004. – 424 с.
Яковлев, И. В. Комбинаторика для олимпиадников / И. В. Яковлев. – М. : МЦНМО, 2016. – 80 c.
Источник