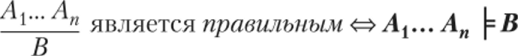Табличный способ проверки умозаключений

Проверка умозаключений табличным методом

Запись f= X означает, что формула X является логическим законом). Выполните упражнения 15—18 из Практикума. Есть другой способ. Вычеркнем все строчки, в которых хотя бы одна из посылок ложна (т.е. 1, 2, 3-ю и 7-ю): Следовательно, если в мире есть справедливость, он не может быть творением злого гения. Если в мире есть справедливость, злые люди не могут быть счастливы. Если мир сотворил злой… Читать ещё >

Проверка умозаключений табличным методом ( реферат , курсовая , диплом , контрольная )

Понятие логического следования является формальным уточнением (конкретизацией) понятия правильного умозаключения (см. гл. 1). Теперь мы дадим такое определение:

Умозаключение является правильным тогда и только тогда, когда из его посылок логически следует его заключение.

Таким образом, вопрос содержательного характера о правильности данного УЗ, состоящего из конкретных высказываний, сводится к вопросу формального характера о наличии отношения логического следования между формулами, логическими формами этих высказываний.

Покажем, как можно осуществлять проверку УЗ табличным методом. Пусть дано такое изящное УЗ (пример В. А. Бочарова и В. И. Маркина):

Если в мире есть справедливость, злые люди не могут быть счастливы.

Если мир сотворил злой гений, то злые люди могут быть счастливы.

Следовательно, если в мире есть справедливость, он не может быть творением злого гения.

Правильно ли оно? Чтобы ответить на этот вопрос, надо, выявив логические формы этих трех высказываний, установить, следует ли третье (заключение) из первых двух (посылок).

Логическая форма данного умозаключения:

где р — «В мире есть справедливость», q — «Злые люди могут быть счастливы», s — «Мир есть творение злого гения» [https://referat.bookap.info, 9].

Строим совместную таблицу истинности для этих трех формул:

Источник

Проверка правильности умозаключений

Правильность умозаключения можно проверить двумя способами.

Во-первых, мы можем построить таблицу истинности и показать, что всякий раз, когда гипотезы истинны, истинно и заключение. Во-вторых, мы можем использовать таблицы истинности для обоснования правил вывода, а затем использовать правила вывода для доказательства справедливости заключения. Длинные умозаключения, как правило, проще обосновывать при помощи правил вывода (см. п. 1.5).

Рассмотрим метод проверки правильности умозаключений, альтернативный методу таблиц истинности. Пока предлагается принять метод на веру, вернувшись к его обоснованию несколько позже. Это непрямой метод, поскольку он направлен на доказательство неправильности умозаключения. В случае успеха такого доказательства это будет свидетельством неправильности умозаключения. Если, предполагая неправильность умозаключения, мы приходим к противоречию, то умозаключение является правильным. Например, рассмотрим умозаключение

A 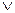B

A 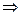C

B 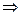C

Если умозаключение неправильное, существуют истинностные значения A, B и C,

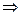
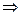
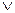
для которых посылки истинны, а заключение ложно. Если заключение ложно, то C ложно. Если B C истинно , а C ложно, то B должно быть ложно. Аналогично, если A C истинно, а C ложно тогда A должно быть ложно. Но тогда A B ложно, что приводит к противоречию с утверждением, что заключение ложно, а посылки истинны. На основании этого делаем вывод, что умозаключение правильно.

Правила вывода

Перечислим некоторые правила вывода, на которые мы будем ссылаться в

а) Правило отделения (Modus Ponens)

A 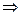B

A 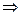B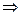

B C

A 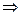C

в) Modus Tollens

A 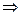B

Источник

Прямые умозаключения логики высказываний

Умозаключения логики высказываний основаны на структуре сложных суждений (на смысле логических связок, объединяющих простые суждения в сложные) и не учитывают внутреннюю структуру простых суждений, входящих в посылки.

Умозаключения логики высказываний бывают прямые и непрямые. Прямыми называются умозаключения, в которых заключение выводится из некоторого множества суждений. Непрямыми являются умозаключения, которые получаются путём преобразования других умозаключений.

Виды простых[2] форм прямых умозаключений логики суждений:

1. Условно-категорические – это умозаключения, в которых одна посылка – условное суждение, а вторая посылка и заключение – суждения категорические. Условно-категорические умозаключения бывают двух разновидностей:

а) утверждающий модус: А®В, А В

б) отрицающий модус: А®В, щВ щА

(В схемах умозаключений над чертой записываются посылки, под чертой – заключение, черта означает «следовательно»; А и В – простые суждения).

Пример 1. Если человек простужен (А), то он болен (В).

Пример 2. Если человек простужен (А), то он болен (В).

Он не простужен (ùА).

Сходные схемы

А®В, В А

и

А®В, ùА ùВ

не являются правильными.

Пример 3. Из посылок «Если человек простужен (А), то он болен (В)» и «Человек болен (В)» вовсе не обязательно следует «Он простужен (А)». «Человек болен» может означать, что у него сломана нога, поднялось давление и т. п. И только с определенной долей вероятности может оказаться, что он болен, потому что простужен. Аналогично вероятным получится заключение и для отрицающего модуса.

2. Разделительно-категорические – это умозаключения, в которых одна посылка – разделительное суждение, а другая посылка и заключение – суждения категорические. Разделительно-категорические умозаключения также бывают двух разновидностей:

а) утверждающе-отрицающая схема:	б) отрицающе-утверждающая схема:
АЪВ, В щА	АЪВ, А щВ	АЪ (Ъ) В, щА В	АЪ (Ъ) В, щВ А

Пример. Отрицающе-утверждающая схема:

Либо мы уходим (А), либо мы остаемся (В).

3. Дилеммы (условно-разделительные силлогизмы) – это умозаключения, в которых две посылки – условные суждения, одна – разделительное, а заключение — либо простое суждение (в простой дилемме), либо сложное разделительное (дизъюнктивное) суждение (в сложной дилемме).

а) простая конструктивная дилемма:	б) простая деструктивная дилемма:
А®С, В®С АЪВ С	А®В, А®С щВЪщС щА
в) сложная конструктивная дилемма:	г) сложная деструктивная дилемма:
А®В, С®D AЪC BЪD	A®B, C®D щBЪщD щAЪщC

Пример. «Если вы будете говорить правду (А), люди проклянут вас (В), а если будете лгать (С), то вас проклянут боги (D). Но вы можете только говорить правду (A) или лгать (C). Значит, вас проклянут боги (D) или люди (B)». Если мы выпишем из этого рассуждения только буквенные обозначения простых суждений, соединив их соответствующими логическими связками, то получим форму сложной конструктивной дилеммы.

Имеется и еще одна форма дилемм – конструктивно-деструктивные, или деструктивно-конструктивные. В этих умозаключениях некоторые из членов разделительной посылки указывают на наличие оснований условных посылок, а некоторые – отрицают следствия (консеквенты) других условных посылок. Например, конструктивно-деструктивной является дилемма вида:

4. Чисто условные умозаключения – это вывод из любого количества посылок, которые представляют собой условные суждения и заключения которых также являются условными суждениями. К этим умозаключениям, в частности, относятся транзитивность импликации и правило контрапозиции.

а) транзитивность импликации:

Пример. «Если лобная кора головного мозга повреждена (A), то взаимодействие личности с внешней средой нарушается (B). В этом случае (B) человек утрачивает реальное восприятие действительности (C), а значит (C), превращается в раба ситуации (D)». Это умозаключение имеет форму транзитивности импликации с тремя посылками:

б) правило контрапозиции:

Пример. «Если человек знает геометрию (А), то он знает теорему Пифагора (В). Следовательно, если он не знает теоремы Пифагора (ùВ), то он не знает геометрии (ùА).

Все приведённые выше формы умозаключений являются правильными, то есть их соблюдение гарантирует правильность заключения при истинности посылок. Иногда эти формы называют правилами соответствующих умозаключений.

Для проверки правильности умозаключений, не сводимых к этим типам, используется, прежде всего, табличный метод. Он основан на том, что между посылками и заключением дедуктивного умозаключения должно существовать отношение логического следования, означающее, что заключение не может быть ложным, если все посылки истинны.

Чтобы проверить правильность умозаключения табличным способом, нужно составить формулу этого умозаключения. Для этого следует:

1) записать посылки и заключение на языке логики суждений;

2) соединить между собой посылки с помощью конъюнкции;

3) присоединить заключение к посылкам с помощью импликации;

4) для полученной формулы составить таблицу истинности.

Умозаключение будет правильным (гарантирующим истинность заключения при истинности посылок) только в том случае, если его формула является тождественно истинной (в последнем столбце таблицы все значения – «истина»).

Пример. «Если философ – дуалист, то он не материалист. Если он не материалист, то он диалектик или метафизик. Он не метафизик. Следовательно, он диалектик или дуалист».

Данное умозаключение довольно сложно привести к какому-либо традиционному типу, поэтому проверим его правильность табличным способом.

Запишем посылки и заключение нашего суждения на языке логики суждений. Обозначим: р – философ – дуалист; q – философ – материалист; r – философ – метафизик; s – философ – диалектик.

Тогда первая посылка – «Если философ – дуалист (р), то он не материалист (ùq)» – на языке логики суждений имеет вид:

Вторая посылка – «Если он не материалист (ùq), то он диалектик (s) или метафизик (r)» – запишется так:

Третья посылка – «Он не метафизик»:

Заключение – «Он диалектик (s) или дуалист (р)»:

Соединяя посылки конъюнкцией (Ù) и присоединяя к ним заключение импликацией (É), получаем формулу:

Для этой формулы составляем таблицу истинности:

p

q

r

s

ùq

ùr

A

B

C

D

E

F

(р®ùq)

sÚr

ùq®B

AÙC

DÙùr

sÚр

D®F

И

И

И

И

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

И

Л

Л

И

И

И

И

Л

И

И

И

Л

И

И

И

Л

И

И

И

И

Л

И

И

Л

Л

И

И

И

Л

И

И

И

И

Л

И

И

И

И

Л

И

Л

И

Л

И

И

Л

Л

И

И

Л

И

Л

И

Л

И

И

И

И

И

И

И

И

И

Л

Л

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

И

И

И

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

Л

Л

Л

И

И

И

И

Л

Л

Л

И

Л

И

Л

И

Л

И

И

И

И

Л

И

И

Л

Л

И

Л

И

Л

И

И

И

И

Л

Л

Л

И

И

Л

Л

Л

И

Л

Л

И

Л

Л

И

И

Л

И

Л

Л

Л

И

И

Л

И

И

И

Л

Л

И

Л

Л

Л

И

И

И

Л

Л

Л

Л

И

И

Л

Л

Л

Л

И

И

И

Л

Л

Л

Л

Л

И

Получилась выполнимая формула, так как последний столбец таблицы истинности содержит и значения «истина», и значения «ложь». Это говорит о том, что умозаключение вероятное.

При проверке правильности умозаключений можно не строить таблицу полностью, а, получив значения истинности посылок и заключения, ограничиваться рассмотрением только тех строк, в которых все посылки принимают значения «истина». Так, в данном примере, получив значения в столбцах 6 (третья посылка), 7 (первая посылка), 9 (вторая посылка) и 12 (заключение), мы могли бы исследовать только строки 6, 7, 8, 14.

Дело в том, что, с одной стороны, вести речь об истинности заключения имеет смысл только при условии истинности посылок. При ложных посылках даже правильное по форме умозаключение не может гарантировать истинности заключения. А, с другой стороны, проверяя правильность умозаключения, мы, по существу, проверяем, соблюдается ли в нем отношение логического следования между посылками и заключением. Оно как раз и состоит в том, что во всех случаях, когда посылки — истинные суждения, заключение — также истинное суждение, и ни в одной строке таблицы не наблюдается случая, когда все посылки истинны, а заключение ложно. При ложной же посылке мы вообще не можем говорить об отношении логического следования.

Источник