Табличный способ логические задачи по математике

Решение логических задач табличным способом

Главным в предлагаемых задачах является способ решения — построение таблицы, строки которой соответствуют элементам одного из рассматриваемых в условии задачи множеств, столбцы — элементам другого, пересечение строки и столбца — комбинации двух элементов разных множеств. С помощью такой таблицы анализируются условия задачи, делаются выводы, проверяется избыточность, полнота и правильность выводов.

Задача 1. После соревнований бегунов на табло появилась надпись:
• Рустам не был вторым.
• Эдуард отстатл от Рустама на два места.
• Яков не был первым.
• Галина не была не первой ни последней.
• Карина финишировала сразу за Яковом.
Кто же победил в этих соревнованиях? Каково было распределение бегунов на финише?

Решение:
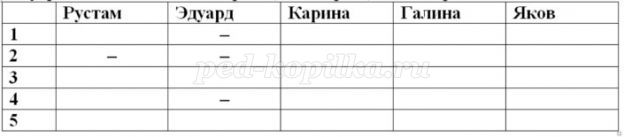
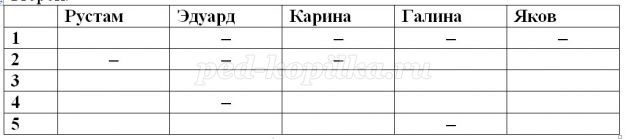
Рисуем таблицу, где столбцы –имена детей, а строки – номера мест. Читаем задачу, пошагово анализируем условие и ставим в таблицу «+», если соответствие установлено и «–», если точно соответствия нет.
Так как Рустам не был вторым и Эдуард отстал от Рустама на два места, то Эдуард не может быть ни первым, ни вторым, ни четвёртым.

Так как Карина финишировала сразу за Яковом, то очевидно, что Яков был четвёртым, а Карина последней и тогда Галина была второй.

Итак, можно выделить
Пять простых шагов на пути поиска решения логических задач.
1. Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты.
2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия.
5. Решение можно найти простым методом последовательных исключений.

Чем больше будете тренироваться, тем лучше у вас это будет получаться. А теперь за дело.

Задача 2.
В субботний вечер Семен, Коля и Витя решили развлечься. У них был выбор: кино, рок-концерт или танцы.
• Семён любит кино, но к танцам менее нетерпим, чем к рок-музыке.
• Коля любит танцевать, но готов пойти в кино скорее, чем на рок концерт.
• Витя любит рок-музыку меньше чем танцы, но кино ему всё-таки не так неприятно, как танцы или концерт.
Поскольку вопрос решатся большинством голосов, то куда, на ваш взгляд отправились эти ребята?
Задача 3.
Трое мальчиков Костя, Фома и Марат дружили с тремя девочками – Женей, Светой и Мариной. Но вскоре компания разделилась на пары, потому, что оказалось:
• Света ненавидит ходить на лыжах.
• Костя, Женин брат часто катается со своей подружкой на лыжах
• А Фома теперь бежит на свидание к Костиной сестре.
С кем же проводит время Марат?

Задача 4.
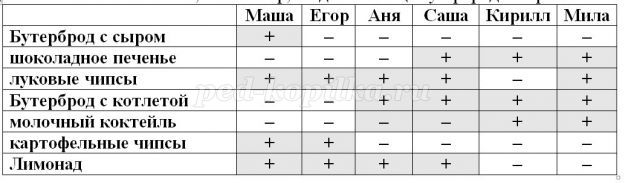
Шестеро друзей в ожидании электрички заскочили в буфет.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад.
Из чего состоял завтрак каждого из друзей?

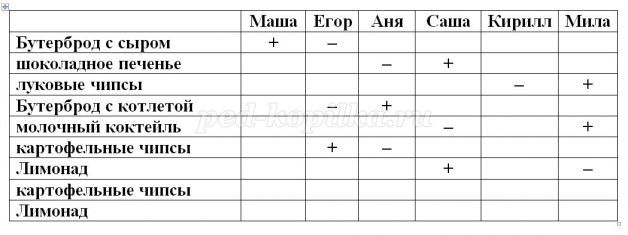
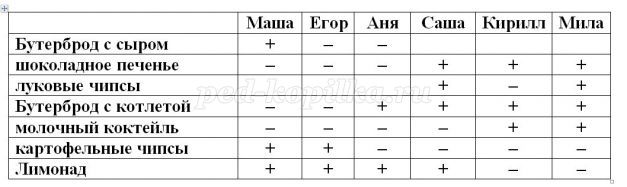
Решение: Так как
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром;
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье;
• Кирилл ел то же, что и Мила, но без луковых чипсов;
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы;
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то:

Задача 5.
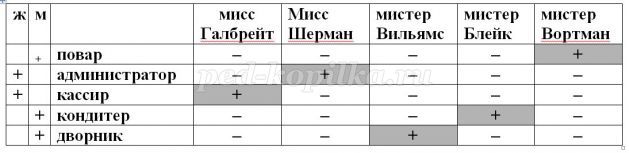
В одном небольшом кафе в смене одновременно работали 5 человек: администратор, повар, кондитер, кассир, дворник. Одновременно на работу выходили мисс Галбрейт, мисс Шерман, мистер Вильямс, мистер Вортман и мистер Блейк. При этом известно, что:
1. Повар – холостяк.
2. Кассир и администратор жили в одной комнате, когда учились в колледже.
3. Мистер Блейк и мисс Шерман встречаются только на работе.
4. Миссис Вильямс расстроилась, когда муж сказал ей, что администратор отказал ему в отгуле.
5. Вортман собирается быть шафером на свадьбе у кассира и кондитера.
Кто на какой должности в этом кафе?

Можно разделить учащихся на группы и каждой группе дать индивидуальное задание или подобрать задачи для каждого ученика.

Задача 1.
Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они ответили:
1) «Коля не занял ни первое, ни четвертое места».
2) “Боря занял второе место”.
3) “Вова не был последним”.
Какое место занял каждый мальчик?
Задача 2.
Три одноклассника — Влад, Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой — физиком, а третий — юристом. Один увлекся туризмом, другой — бегом, третий — регби.
1. Юра сказал, что, на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
2. Врач сказал, что он разделяет увлечение коллеги.
3. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Кто чем любит заниматься в свободное время и у кого какая профессия?
Задача 3.
Три друга — Иван, Дмитрий, Степан преподают различные предметы (химию, литературу, физику) в школах Москвы, Калининграда и Перми. Известно:
1) Иван работает не в Москве, а Дмитрий не в Калининграде;
2) москвич преподает не физику;
3) тот, кто работает в Калининграде, преподает химию;
4) Дмитрий преподает не литературу.
Какой предмет и в каком городе преподает каждый из товарищей?
Задача 4.
Четыре девочки Маша, Таня, София и Полина взяли в кафе сок. Каждая из них покупал только один сок, причем две из них купили сок яблочный, одна виноградный, и одна – грушевый. Известно, что у Маши и Тани разные вкусы. Разные соки взяли Маша с Софией, Полина с Софией, Полина с Машей и Таня с Софией. Кроме того известно, что Маша купила не грушевый сок. Определить, какой сок пила каждая из них.
Задача 6. (Один из вариантов «Задачи Эйнштейна»)
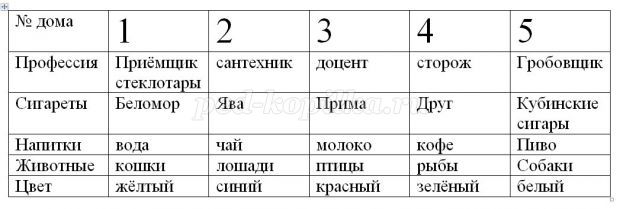
Пять домов стоят вдоль дороги, один за другим.
1. Доцент живёт в красном доме.
2. Гробовщик держит собак.
3. Сантехник пьёт чай.
4. Зелёный дом слева от белого.
5. Хозяин зелёного дома пьёт кофе.
6. Любитель «Примы» держит птицу.
7. Хозяин жёлтого дома курит «Беломор канал».
8. В центральном доме любят молоко.
9. Приёмщик стеклотары живёт в первом доме.
10. Курящий «Яву» сосед хозяина кошек.
11. Хозяин лошадей – сосед курящего «Беломор».
12. Любитель пива курит «Кубинские» сигары.
13. Ночной сторож предпочитает сигареты «Друг».
14. Приёмщик стеклотары живёт рядом с синим домом.
15. Курящий «Яву» сосед пьющего воду.
Кто держит рыб? (номер дома, цвет профессия, напитки)
Решение:

Составить логическую задачу самостоятельно.
Удачи вам!

Задачи, составленные моими учениками.
Иванова Светлана, 7«Б» кл.
На дискотеку пошли 4 девочки: Маша, Оля, Рита. На медленный танец их приглашали Сергей, Рома, Саша, Паша. Кто с кем танцевал, если:
1) Оля не танцевала с Пашей;
2) Таня не танцевала с Пашей и Романом;
3) Рита танцевала с Ромой;
4) Оле понравился Сергей, но она не танцевала с ним.

Маякова Оксана, 9«А» кл.
Бизнесмены Боря Вова Гриша и Гена зарабатывают сумасшедшие деньги, их фамилии засекречены, но удалось их узнать, правда непонятно какая кому принадлежит. Их фамилии: Иванов, Енин, Сидоров, Петров. Так же наши шпионы выяснили:
1) Боря и Петров не имеют личные самолёты.
2) Гриша и Иванов вообще ничего личного не имеют, кроме счетов в швейцарском банке.
3) Гена теперь важнее Енина, хотя Енин и имеет личный самолёт.
4) Петров важнее Енина.
У кого какая фамилия?

Конева Ксения, 9«А» кл.
Четыре подружки: Даша, Маша, Ольга и Таня ходили в магазин покупать подарки. И все подарки разные. Блокнот, альбом, брелок, и книга. На вопрос кто какие подарки купил, они ответили так:
1) Даша и Оля не знали кто купил блокнот;
2) Оля сказала, что Даша и Маша вместе с ней посещали магазин, где продают брелки.
3) Даша не покупала альбом.
Кто какой подарок купил?

Источник

Презентация «Табличный способ решения логических задач»

Описание презентации по отдельным слайдам:

Предмет математики настолько серьезен, что нельзя упускать случая сделать его немного занимательным. Блез Паскаль

Эмблема мастер-класса: Говорят уравнение вызывает сомнение, но итогом сомнения может быть озарение!

Основные приемы и методы решения логических задач Теория, мой друг, суха, но зеленеет жизни древо. И.В.Гете Известно несколько различных способов решения логических задач: Метод рассуждений; Метод таблиц; Метод графов; Метод блок-схем; Метод бильярда; Метод кругов Эйлера.

Остановимся подробно на табличном способе решения логических задач

Решение логических задач табличным способом Задача 1. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: 1. Смит самый высокий; 2. играющий на скрипке меньше ростом играющего на флейте; 3. играющие на скрипке и флейте и Браун любят пиццу; 4. когда между альтистом и трубачом возникает ссора, Смит мирит их; 5. Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?

Решение 1. Смит самый высокий; 2. играющий на скрипке меньше ростом играющего на флейте; 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун Смит Вессон

Решение 3. играющие на скрипке и флейте и Браун любят пиццу; 0 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун Смит 0 Вессон

Решение 4. когда между альтистом и трубачом возникает ссора, Смит мирит их; 0 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 Смит 0 Вессон

Решение 5. Браун не умеет играть ни на трубе, ни на гобое. 0 0 1 1 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 Смит 0 0 0 Вессон

Решение Так как музыкантов трое, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют. 1 1 1 1 0 0 0 0 Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе. Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 1 1 0 0 Смит 0 0 0 0 Вессон

Задача 2 На конгрессе встретились четверо ученых: физик, биолог, историк и математик. Каждый учёный владел двумя языками из четырёх (русским, английским, французским и итальянским), но не было такого языка, на котором могли бы разговаривать все четверо. Есть только один язык, на котором могли вести беседу сразу трое. 1.Никто из учёных не владеет и французским, и русским языками. 2. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 4. Физик, биолог и математик могут разговаривать на одном языке. Какими двумя языками владеет каждый учёный?

1.Никто из учёных не владеет и французским, и русским языками. 2. Хотя физик не говорит по-английски, он может служит переводчиком, если историк и биолог захотят побеседовать. Решение 0 Языки профессия Русский Аанглийский Французский Итальянский Математик Биолог Физик Историк

Решение 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 4. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 0 1 1 0 Языки профессия Русский Английский Французский Итальянский Математик Биолог Физик 0 Историк

Решение 4. Физик, биолог и математик могут разговаривать на одном языке. 1.Никто из учёных не владеет и французским, и русским языками. 0 0 Языки профессия Русский Английский Французский Итальянский Математик 0 Биолог 0 Физик 1 0 Историк 1

Решение 4. Физик, биолог и математик могут разговаривать на одном языке. Какими двумя языками владеет каждый учёный? 1 1 1 1 Языки профессия Русский Английский Французский Итальянский Математик 0 Биолог 0 Физик 1 0 0 Историк 1 0 0

Решение 2. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 0 1 0 1 Ответ: математик – английский и итальянский; биолог – французский и итальянский; физик – русский и итальянский; историк – русский и английский. Языки профессия Русский Английский Французский Итальянский Математик 0 1 Биолог 0 1 Физик 1 0 0 1 Историк 1 1 0 0

Алгоритм решения Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты. 2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов. 3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок. 4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия. 5. Решение можно найти простым методом последовательных исключений.

Тренировочные задания Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия.

Ответ на задачу Имя Юра Тимур Влад Профессия Увлечение

Ответ на задачу Имя Юра Тимур Влад Профессия физик врач юрист Увлечение бег туризм регби

“Смотреть – не значит видеть!” k = n = m = 1 4 7

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-052911

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

В Осетии студенты проведут уроки вместо учителей старше 60 лет

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник