Табличный способ алгоритма пример

Способы записи алгоритмов

На практике применяются алгоритмы следующих типов:

Линейные алгоритмы

Это алгоритмы, у которых последовательность операций при исполнении совпадает с порядком их следования в записи алгоритма и не зависит от конкретных значений исходных данных. С помощью таких алгоритмов реализуются задачи типа:

Y = А*Х+В

разветвляющиеся, ветвящиеся алгоритмы. Такие алгоритмы
используются для решения задач, в которых заложена операция выбора одной из формул, в зависимости от заданного
значения переменной. Такие алгоритмы используются при
решение задач, типа:

Y=Ln x, при x>=1

Y=1-x, при x n

Для записи алгоритмов обычно используют табличный, словесный и схематичный способы записи.

Табличный способ записи алгоритмов

Табличный способ записи алгоритмов применяется, когда требуется вычислить не одно, а несколько значений одного и того же выражения для различных значений входных величин.

Например, требуется вычислить площадь поверхности цилиндрического тела по формуле:

S=3.14*(D*H+D 2 /2)

где D — диаметр, Н — высота.

Табличный алгоритм вычисления площади поверхности тела по указанной формуле представлен в таблице:

D	H	3.14*D	3.14*D 2	3.14*D 2 /2	3.14*D*H	S
6	4	18,84	113,04	56,52	75,36	131,88
5	10	15,7	78,5	39,25	157	196,25
10	12	31,4	314	157	376,8	533,8

Словесный способ записи алгоритмов

Одна из самых распространенных форм представлении алгоритмов — словесная форма. Особенностью словесной представления алгоритма является то, что таким cnocoбом могут быть описаны любые алгоритмы, в том числе и вычислительные.

Опишем последовательность действий для вычислений по формуле:

Y=(6*x+25)/2.

1) Прочитаем заданное значение X;

2) Умножим X на 6;

3) К результату второго действия прибавим 25;

4) Результат третьего действия разделим на 2;

5) Запишем значение результата Y;

В результате получили словесную запись линейного вычислительного алгоритма.

В приведенном вычислительном алгоритме X является входной величиной (исходным значением, аргументом), а Y выходной величиной (результатом).

В словесной записи алгоритма, если при исполнении текущего предписания не указывается явно номер очередного предписания, происходит автоматический переход к предписанию, следующему за данным в порядке возрастания номеров.

После исполнения предписания с наибольшим номером, процесс выполнения алгоритма заканчивается.

Для удобства рекомендуется заканчивать запись словес о алгоритма специальным предписанием «конец».

При записи вычислительных алгоритмов удобно использовать специальный знак присваивания :=. Этот знак используется для записи специальной операции операции присваивания. Смысл операции присваивания состоит в том, что некоторой переменной, имя которой указывается слева, присваивается значение некоторого выражения, указанного справа.

Например, предписание, вида Y:=X читается так: «переменной Y присвоить значение X». Если X — является формулой, тогда нужно выполнить все действия, предусмотренные формулой и полученный результат (число) присвоить переменной Y.

Операция присваивания может быть обозначена и обычным знаком равенства или стрелками: A:=D*B, A=D*B, A->D*B.

Используя знак операции присваивания и вспомогательные переменные, в которых будут запоминаться промежуточные значения, можно сделать запись приведенного выше словесного алгоритма значительно компактнее:

После составления словесного алгоритма необходимо провести контроль правильности составления алгоритма. Проверка алгоритма в таблице состоит в том, что выбираются конкретные исходные данные и составленный алгоритм выполняется в строгом соответствии с записанными предписаниями.

Таблица контроля правильности алгоритма вычисления Y=(6*X+25)/2

Шаги алгоритма	Аргумент X	Промежуточная величина А	Промежуточная величина B	Результат Y	Пояснения
1	2	чтение X
2	12
3	37
4	18.5
5	запись 18.5
6	остановка

Важное свойство операции присваивания состоит в том, что одна и та же переменная может находиться и слева и справа от знака присваивания, т.е. можно записать

А := А+В.

Такая запись означает, что к значению переменной А, которое она имела до начала выполнения операции присваивания, прибавляется значение переменной В и полученное в результате значение присваивается переменной А (становится новым значением переменной А). Прежнее значение переменной А при этом пропадает.

Используя это свойство операции присваивания, можно отказаться от использования избыточных промежуточных переменных.

Тогда запись алгоритма вычисления Y будет иметь следующий вид:

В приведенном примере можно не использовать ни одной вспомогательной переменной, т.к. для хранения промежуточных результатов достаточно использовать одну переменную Y.

Таблица проверки правильности алгоритма наглядно показывает механизм проведенных присваиваний.

Таблица контроля правильности алгоритма вычисления Y=(6*x+25)/2 без избыточных вспомогательных переменных

Источник

Табличный способ записи алгоритма на примере задачи о стиральной машине

На примере решения этой простой задачи научимся составлять алгоритмы в виде таблицы:

«В машину вмещается 10 л воды. У неё есть две кнопки — красная и синяя. Если нажать на красную, то в машину наливается 3 л воды, а если на синюю, то выливается 2 л воды. В какой последовательности надо нажимать на кнопки, чтобы налить полную машину воды?»

Просмотр содержимого документа
«Табличный способ записи алгоритма на примере задачи о стиральной машине»

(рекомендуется для учащихся 4-х классов)

Тема занятия: «Табличный способ записи алгоритма на примере задачи о стиральной машине».

1. Научить составлять алгоритм в виде таблицы.

2. Развитие логического мышления с помощью поставленной задачи в задании «Стиральная машина».

1. Организационный момент.

2 Повторение понятия «алгоритм».

3. Постановка задачи: наполнить водой стиральную машину.

4. Составление алгоритма заполнения стиральной машины водой в виде таблицы.

5. Игра буддийских монахов на компьютере.

6. Подведение итогов.

На уроке используется цветная таблица «Стиральная машина». На ней изображена стиральная машина, в которой:

1) Слишком мало воды.

2) Слишком много воды.

Таблица, в которой с помощью кнопок (синей и красной) показан порядок действий для наполнения стиральной машины водой (10 л).

В машину вмещается 10 л воды. У неё есть две кнопки — красная и синяя. Если нажать на красную, то в машину наливается 3 л воды, а если на синюю, то выливается 2 л воды. В какой последовательности надо нажимать на кнопки, чтобы налить полную машину воды?

Учитель: Что произойдёт, если наполнить так, как записано в таблице.

Ученик: При составлении алгоритма допущена ошибка – вариант «слишком много воды».

Учащимся предлагается найти ошибку и объяснить её.

Учитель: Самостоятельно составьте правильный алгоритм в виде такой же таблицы для заполнения стиральной машины водой в тетрадях.

Учитель: Чем отличаются алгоритмы №1 и №2?

Правильность составления алгоритма проверяем у доски, обсуждая в классе. Отмечаю наиболее активно работавших учащихся.

Игра буддийских монахов – «Ханойская башня».

Давайте поиграем в игру буддийских монахов, установленную на компьютере.

Игра заключается в следующем: на подставке закреплены три стержня. На левый стержень нанизано несколько колец разного размера – внизу самое большое кольцо, на нём поменьше, сверху ещё меньше и т.д. Надо, перемещая по одному кольцу со стержня на стержень, надет все кольца на правый. Как надо перекладывать кольца, если на левом стержне:

3. четыре кольца

После выполнения задания предлагается учащимся заполнить таблицу в рабочих тетрадях:

Источник

Способы представления алгоритмов

Алгоритмом (algorithm) называют чёткое описание последовательности действий, направленных на решение конкретной задачи. О важности и типах алгоритмических последовательностей сказано уже немало. В этой статье пойдёт речь о способах их представления при записи алгоритмов.

Словесный способ

Словесное описание алгоритма предполагает наличие некого словесного перечня действий. Пример — вам говорят что-то типа следующего: «Вычислите Z при условии, что Z = X + Y, когда X равен 0,89, а Y равен 1,286. Полученное значение Z следует возвести в куб и вычислить корень».

Можно представить ситуацию туристического посещения незнакомого города. Когда вы спрашиваете, как пройти в интересующее место, вам объясняют, что надо через 100 метров повернуть направо, потом пройти прямо, пока не увидите перед собой здание кинотеатра, далее потребуется перейти дорогу, повернуть налево и не сворачивая идти до нужного объекта.

Все эти примеры можно назвать словесным способом представления. У такого способа есть недостаток: отсутствие наглядности выполнения процесса и чёткой формализации объектов алгоритма.

Формульно-словесный способ

При использовании формульно-словесного способа инструкции задаются более чётко. Этот тот случай, когда словесные пояснения сопровождаются перечнем конкретных действий, плюс эти пояснения характеризуются наличием формальных символов и выражений (формул).

Для примера составим формульно-словесный алгоритм вычисления выражения: z=2∙x–(y+6): • вводим значения х и y; • находим сумму (y+6); • находим произведение (2∙x); • вычисляем z как разность уже полученных выше значений: z=2∙x–(y+6); • выводим z как результат вычисления выражения.

Это более компактный и лаконичный метод, он нагляднее, но всё же строго формальным не является.

Табличный способ

В случае применения табличного метода алгоритм задаётся в виде входных данных: расчётных форм и таблиц. Способ широко применяется в экономических расчетах. Исходные данные, как и результаты, заносятся в заголовки столбцов используемой таблицы. Простейший пример такого способа представления — та же таблица умножения:

Графический способ

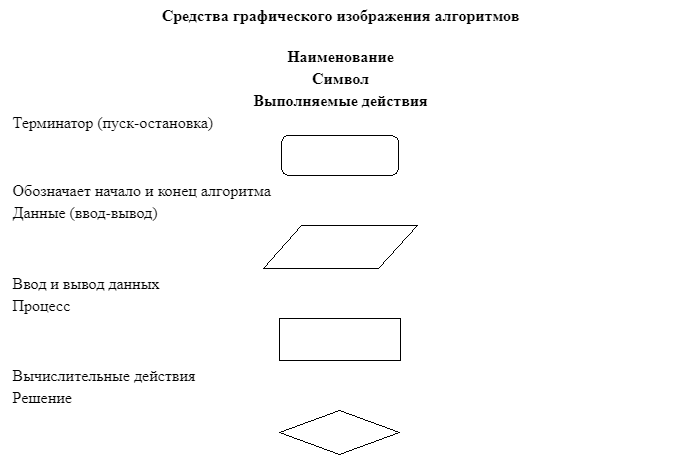
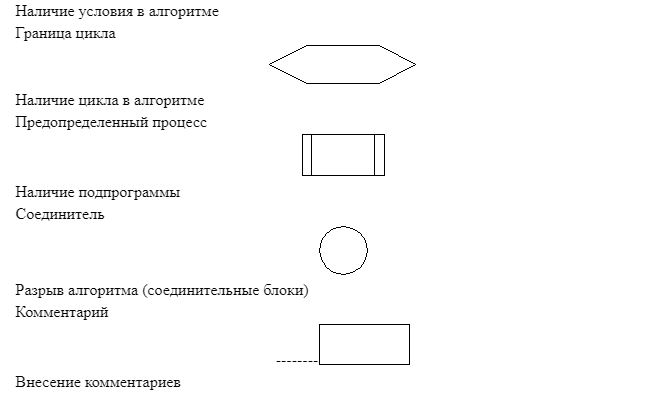
Этот метод ещё называют способом блок-схем. В данной ситуации каждый этап прохождения алгоритма представляется в виде геометрических фигур — так называемых «блоков», причём конкретная форма фигур зависит от выполняемой операции. Существует стандарт, регламентирующий размеры используемых графических блоков, а также их отображение, функции, формы и взаимное расположение. Направление работы алгоритма показывают линии соединения блоков.

Другое название способа — визуальное представление. При проектировании алгоритмов, представленных графически, придерживаются ряда правил: • в начале алгоритма располагаются блоки ввода значений (входные данные); • после ввода значений располагаются блоки обработки и блоки условия; • алгоритм завершается блоками вывода значений, полученных в результате работы алгоритма (выходные данные); • должен быть лишь один блок начала и один — окончания; • межблочная связь указывается линиями (направленными либо ненаправленными); • вычислительные формулы, данные и логические выражения размещаются внутри соответствующих блоков; • возможно наличие комментариев в виде выносок.

Графический способ представления имеет практическое значение и используется не только в случае программирования. Его применяют при составлении информационных и структурных схем, инфографики и в иных ситуациях, когда нужно обеспечить чёткую визуализацию данных и графически отобразить последовательность расположения объектов алгоритма.

Создание блок-схемы алгоритма — важный и нужный этап решения поставленной задачи. Но при некоторых обстоятельствах этот этап можно считать промежуточным, так как в таком виде описанный алгоритм невозможно выполнить средствами ЭВМ. Зато графический способ представления значительно облегчает процесс дальнейшего создания компьютерной программы. О ней ниже.

Программный способ (текстовая запись)

Программа представляет собой алгоритм, который записан как последовательность команд. Речь идёт о командах, понятных компьютеру, для чего используются различные языки программирования, представляющие собой системы кодирования предписаний с правилами их применения. Языки программирования характеризуются строго определённым синтаксисом, то есть свободное толкование конструкций не допускается.

В случае программного способа представления алгоритмическая последовательность записывается в виде компьютерной программы с высокой степенью формализации. В результате появляется возможность решать прикладные задачи.

Пример — простейший алгоритм сложения 2-ч чисел, который записан средствами языка программирования Qbasic:

О взаимодополнении способов представления

Способы, представленные выше, нередко являются взаимодополняемыми: — на этапе обсуждения используются словесные и словесно-формульные способы; — на этапе проектирования рекомендуется использовать графические алгоритмы (графическое представление); — на этапе проверки возможно табличное описание; — на этапе непосредственного применения и решения прикладных задач используют текстовую запись, представленную в виде компьютерной программы.

Источник