Свой способ записывать арифметические действия

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

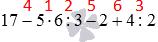
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Источник

Способы записи решения задач.
учебно-методический материал по математике

Учебный-методический материал поможет учителю при работе с текстовыми задачами на уроках математики.

Скачать:

Вложение	Размер
sposoby_zapisi_resheniya_zadach.doc	26 КБ

Предварительный просмотр:

Способы записи решения задач.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач в этом случае оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением. В начальных классах используются различные формы записи решения задач арифметическим способом: по действиям; по действиям с пояснением; с вопросами; выражением.

У мальчика было 90 книг. 28 он поставил на первую полку. 12 — на вторую, остальные — на третью. Сколько книг на третьей полке?

а ) Решение по действиям:

Ответ: 50 книг на третьей полке.

б ) По действиям с пояснением:

1) 28+12=40 ( к.) — на первой и второй полках вместе,

2) 90-40=50 ( к.) — на третьей полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

Ответ: 50 книг на третьей полке,

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так: 90-(28+12)=50 (к.)

Ответ: 50 книг на третьей полке.

Не следует путать такие понятия, как: решение задачи различными способами (практический, арифметический, графический, алгебраический); различные формы записи арифметического способа решения задачи (по действиям, выражением, по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомыми, а следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90-28 = 62 ( к.) — на второй и третьей полке,

2) 62-12 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке.

В качестве арифметического способа можно рассматривать и такое решение

1) 90-12 = 78 ( к.) — на первой и третьей полке,

2) 78-28 = 50 ( к.) — на третьей полке.

Ответ: 50 книг на третьей полке

По теме: методические разработки, презентации и конспекты

Урок математики во 2 классе «Решение задач графическим способом»

Урок развивает умение решать текстовые задачи графическим способом; развивает математическую речь, логическое мышление; воспитывает интерес к точным наукам, аккуратность, чувство товарищества, в.

Конспект урока русского языка на тему: «Выявление орфографической задачи на месте сочетаний [сн], [с\’н\’] и способы её решения.

Тема урока: «Выявление орфографической задачи на месте сочетаний [сн], ]с\’н\’] и способы её решения»Цель урока: усвоение основ орфограммНа уроке ребята узнают, что некоторые звуки руссого языка трудно .

Мастер-класс » Комбинаторные задачи и способы их решения»

ФГОС второго поколения начального общего образования определяет новые требования к уровню подготовки младших школьников, что предполагает необходимость переосмысления учителями начальной школы как сам.

Конспект урока математики по теме: «Решение задач разными способами»

Конспект урока с использованием деятельностного подхода.

Конспект урока по математике в 3 классе «Решение задач разными способами»

Конспект урока по математике в 3 классе.

Методика записи краткого условия и решения задачи.

Уроки счета для глубоко умственно отсталых связаны с формированием разнообразных умений и навыков умственной и учебной деятельности способствуют коррекции недостатков познавательной деятельности и лич.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова) Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.

Конспект урока математики 4 класс (система Д.Б.Эльконина – В.В.Давыдова)Тема. Анализ средств для самоконтроля при составлении краткой записи и решении задач.Тип урока. Урок рефлексии.Цель. Форми.

Источник

Урок 9. 10 простейших математических приемов

Рассмотрев самые важные вопросы и наиболее трудоемкие моменты в процессе обучения детей счету, теперь мы можем позволить себе немного расслабиться. Сегодня мы познакомимся с десятью простейшими математическими приемами, которые, во-первых, помогут осознать вашему ребенку, что математика – это просто и интересно, а во-вторых, научат его получать удовольствие от вычислений. Впрочем, и вам самим, как родителям, будет полезно освежить в памяти арифметические знания и, быть может, открыть для себя нечто новое.

Представленные ниже математические приемы улучшат навыки вашего драгоценного чада и ускорят его выполнение математических приемов в уме. Далее мы рассмотрим:

Умножение на «4»

Умножение на «4» можно назвать одним из простейших приемов, несмотря на то, что некоторые не замечают его очевидности. Хитрость этого приема состоит в том, что умножаемое число требуется умножить на «2», а потом еще раз умножить на «2». Другой вариант: умножить число на «2», а затем к результату прибавить этот же результат.

ПРИМЕР (иллюстрирует оба варианта):

67 х 4 (67х 2) + (67 х 2) 134 + 134 268

Умножение на «5»

Многие дети без каких-либо затруднений могут запомнить таблицу умножения на «5». Однако когда дело касается больших чисел, а не простых примеров, нередко возникают затруднения. Но сложным решение кажется лишь на первый взгляд, т.к. есть очень простой прием.

Попробуйте сами: возьмите какое-нибудь число, которое требуется умножить на «5», и поделите его на «2», т.е. разделите пополам. Если в итоге у вас получится целое число, добавьте в конце «0», а если число не целое, то не придавайте большого значения запятой (пропустите ее), а просто припишите «5» в конце. Этот прием работает безотказно.

2 464 х 5 (2 464/2) + «0» (в конце, т.к. при делении получается целое число) 12 320

3 747 х 5 (3 747/2) + «5» (т.к. при делении получается дробное число) 1 873,5 (убираем запятую и прибавляем 5) 18 735

Умножение на «9»

Умножить на «9» так же просто, но это касается только тех случаев, когда на «9» умножается любое другое число от «1» до «9». Чтобы произвести такое вычисление, нужно сначала посмотреть на свои ладони с вытянутыми пальцами. Теперь загните один палец, соответствующий умножаемому числу, к примеру, если умножаете «4», загните безымянный палец левой руки (он четвертый по счету слева). Далее посчитайте, сколько пальцев осталось до согнутого – в нашем случае («4» х «9») осталось три пальца. Теперь посчитайте, какое количество пальцев осталось после согнутого – в нашем случае осталось шесть пальцев. Вот вам и ответ: число «36».

Умножение на «11»

Скорее всего, ваш ребенок уже знает, что если умножать какое-то число на «10», к этому числу потребуется добавить ноль. Но и любое двузначное число умножить на «11» не составляет никакой проблемы. Это способ мы уже рассматривали в одном из уроков, но в нашей «коллекции» простых математических приемов он лишним не будет.

Например, вам требуется умножить «54» на «11». Возьмите число «54» и поставьте цифры так, чтобы между ними осталось пустое место. В нашем случае получится «5__4». Далее сложите эти две цифры (т.е. «5» + «4»), а результат вставьте между цифр «5» и «4». В итоге получится ответ «594».

Если при сложении двух цифр у вас получается двузначное число, требуется запомнить вторую цифру, а единичку добавить к первой цифре. К примеру, вам нужно умножить «87» на «11». Сначала разделяем «8» и «7», чтобы получилось «8__7». Затем складываем «8» и «7» и получаем «15». Теперь запоминаем «5», а «1» добавляем к первой цифре нашей пары, т.е. к «8», после чего вставляем между цифрами «5», которую запомнили. В итоге получаем результат «957».

Деление на «5»

Операции с делением чисел на «5» могут показаться очень сложными для ребенка, однако в действительности осуществляются они совсем просто. Все, что требуется сделать, – это умножить число на «2», а затем поставить запятую перед последней цифрой.

423/5 423 х 2 (1-й этап) 846 + «,» перед последней цифрой (2-й этап) 84,6

3 867/5 3 867 х 2 (1-й этап) 7 734 + «,» перед последней цифрой (2-й этап) 773,4

Вычитание из «1000»

Для выполнения операции вычитания из «1000» следует применять простейшее правило: нужно отнимать от «9» каждую цифру, кроме последней, т.к. последнюю цифру нужно отнимать от «10».

3-й этап: 10 – 6 4

Итого: 1000 – 736 264

Сложное умножение

Если вашему ребенку необходимо перемножить большие числа, и если одно из этих чисел является четным, научите его перегруппировке, посредством которой можно быстро получить нужный ответ. При перегруппировке первое (четное) число делится на два, а второе (любое) – умножается на два.

64 х 250 32 х 500 16 х 1 000 16 000

28 х 125 14 х 250 7 х 500 3,5 х 1 000 3 500

Быстрое возведение в квадрат

Данный прием позволяет в мгновение ока возвести в квадрат любое число, оканчивающееся на «5». Выполняется так: первая цифра умножается на туже самую цифру + «1», а в самом конце дописывается «25».

35² (3 х (3+1)) + «25» в конце (3 х 4) + «25» в конце 1 225

95² (9 х (9+1)) + «25» в конце (9 х 10) + «25» в конце 9 025

Подсчет чаевых

Этот приемчик можно использовать, когда, например, вы с ребенком покушали в ресторане, и хотите оставить официанту 15% чаевых. Попросите свое чадо самостоятельно посчитать, сколько денег вы должны оставить. Выполняется всего несколько действий: сначала нужно определить 10% от суммы чека, для чего требуется разделить ее на «10», а затем прибавить к результату еще половину этого же результата.

Вы потратили в ресторане 1 370 рублей. 10% от этой суммы составит 137 рублей, а половина этой суммы составит 68,5 рублей. В итоге 137 + 68,5 205,5 рублей – именно столько вы оставите официанту.

Систематизированные правила умножения

В этом блоке мы предлагаем вашему вниманию сразу несколько хороших правил быстрого умножения:

• Чтобы умножить на «5»: нужно умножить число на «10», а затем разделить на «2»

ПРИМЕР: 25 х 5 (25 х 10)/2 250/2 125

• Чтобы умножить на «6»: нужно умножить число сначала на «3», а затем умножить на «2»

ПРИМЕР: 25 х 6 (25 х 3) х 2 75 х 2 150

• Чтобы умножить на «9»: нужно умножить число на «10», а затем отнять то же самое число

ПРИМЕР: 25 х 9 (25 х 10) – 25 250 – 25 225

• Чтобы умножить на «12»: нужно умножить число на «10», а затем два раза прибавить то же самое число

ПРИМЕР: 25 х 12 (25 х 10) + 25 + 25 250 + 50 300

• Чтобы умножить на «13»: сначала нужно умножить число на «3», затем умножить это же число на «10», а потом сложить вместе полученные результаты

ПРИМЕР: 25 х 13 (25 х 3) + (25 х 10) 75 + 250 325

• Чтобы умножить на «14»: сначала нужно умножить число на «4», затем умножить это же число на «10», а потом сложить вместе полученные результаты

ПРИМЕР: 25 х 14 (25 х 4) + (25 х 10) 100 + 250 350

• Чтобы умножить на «15»: нужно умножить число на «10», а затем прибавить к нему половину полученной суммы

ПРИМЕР: 25х 15 (25 х 10) + половина результата 250 + 125 375

• Чтобы умножить на «16»: нужно умножить число на «2» четыре раза или умножить число на «8», а затем результат умножить на «2»

ПРИМЕР: 25 х 16 (25 х 2) х2 х 2 х 2 (50 х 2) х 2 х 2 (100 х 2) х 2 200 х 400 или (25 х 8) х 2 200 х 2 400

• Чтобы умножить на «17»: сначала нужно умножить число на «10», затем это же число нужно еще раз умножить на «10», а потом сложить два результата и из полученной суммы трижды вычесть исходное число

ПРИМЕР: 25 х 17 (25 х 10) + (25 х 10) – 25 – 25 – 25 (250 + 250) – 25 – 25 – 25 500 – 25 – 25 – 25 425

• Чтобы умножить на «18»: сначала нужно умножить число на «10», затем это же число нужно еще раз умножить на «10», а потом сложить два результата и из полученной суммы дважды вычесть исходное число

ПРИМЕР: 25 х 18 (25 х 10) + (25 х 10) – 25 – 25 (250 + 250) – 25 – 25 500 – 25 – 25 450

• Чтобы умножить на «19»: сначала нужно умножить число на «10», затем это же число нужно еще раз умножить на «10», а потом сложить два результата и из полученной суммы вычесть исходное число

ПРИМЕР: 25 х 19 (25 х 10) + (25 х 10) – 25 (250 + 250) – 25 500 – 25 475

• Чтобы умножить на «24»: нужно умножить число на «8», а затем результат умножить на «3»

ПРИМЕР: 25 х 24 (25 х 8) х 3 200 х 3 600

• Чтобы умножить на «27»: нужно умножить число на «30» (или три раза умножить на «10 и сложить результаты»), а затем от суммы трижды отнять исходное число

ПРИМЕР: 25 х 27 (25 х 30) – 25 – 25 – 25 750 – 25 – 25 – 25 675 или ((25 х 10) + (25 х 10) + (25 х 10)) – 25 – 25 – 25 (250 + 250 + 250) – 25 – 25 – 25 750 – 25 – 25 – 25 675

• Чтобы умножить на «45»: нужно умножить число на «50» (или пять раза умножить на «10 и сложить результаты»), а затем от суммы пять раз отнять исходное число

ПРИМЕР: 25 х 45 (25 х 50) – 25 – 25 – 25 – 25 – 25 1 250 – 25 – 25 – 25 – 25 – 25 1 125 или ((25 х 10) + (25 х 10) + (25 х 10) + (25 х 10) + (25 х 10)) – 25 – 25 – 25 – 25 – 25 (250 + 250 + 250 + 250 + 250) – 25 – 25 – 25 – 25 – 25 1 250 – 25 – 25 – 25 – 25 – 25 1 125

• Чтобы умножить на «90»: нужно умножить число на «10», а затем вычесть исходное число и дописать в конце «0» к результату

ПРИМЕР: 25 х 90 (25 х 10) – 25 + «0» (в конце) 250 – 25 + «0» (в конце) 2 250

• Чтобы умножить на «98»: нужно умножить число на «100» и дважды вычесть исходное число

ПРИМЕР: 25 х 98 (25 х 100) – 25 – 25 2 500 – 25 – 25 2 450

• Чтобы умножить на «99»: нужно умножить число на «100» и вычесть исходное число

ПРИМЕР: 25 х 99 (25 х 100) – 25 2 500 – 25 2 475

И, напоследок, в качестве дополнительного полезного материала мы расскажем вам о том, как легко научить ребенка подсчету процентов, ведь этот навык тоже может пригодиться и в обучении, и в жизни.

Как быстро считать проценты

Нередко случаются ситуации, когда нужно вычислить, например, 8% от «400». Ребенку может представляться достаточно трудной задачей. Поэтому изначально вы должны ему объяснить, что 100% – это «100». Получается, что те же 8% от «100» равны «8», а если взять 41,88% от «100», тоже будет 41,88. Но это только для каждой сотни. Как же это может помочь на практике? Давайте рассмотрим задание про 8% от «400».

В нашем случае 8% от «100» будет «8», но сотни у нас четыре, значит и от всех остальных «100» 8% будет «8». В итоге «8 х 4» (или «8 + 8 + 8+ 8») равно «32», т.е. 8% от «400» – это 32%. Все просто. По аналогии можно вычислить и проценты из «200», «300» и т.д. Но если число менее сотни, то нужно убрать «0» (если «0» имеется) и добавить слева от последней цифры запятую.

7% от 200 7 х 2 (или 7 + 7) 14

6% от 500 6 х 5 (или 6 + 6 + 6 + 6 + 6) 30

8% от 35 8 х 35 (или 8 + 8 + 8 + 4) 280 (убираем «0» и добавляем запятую слева от последней цифры) 2,8%

9% от 25 9 х 25 (или 9 + 9 + 4,5) 225 (добавляем запятую слева от последней цифры) 2,25%.

На письме все это может показаться слегка запутанным, но при регулярных тренировках ваш ребенок научится выполнять эти действия быстро, причем даже без записи на бумаге.

На этом мы заканчиваем часть курса, посвященную обучению детей счету. Занимайтесь, тренируйтесь, не ленитесь, и результата придется ждать недолго. Но чтобы развитие было полноценным, вы, конечно же, должны и учить свое чадо не только читать и считать, но еще и писать. Заключительный блок курса посвящен именно этой теме, и состоит так же из десяти уроков.

Желаем успехов вам и вашему ребенку!

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник